二叉查找树
1. 定义(Binary Sort Tree)
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 任意节点的左、右子树也分别为二叉查找树
- 没有键值相等的节点
简单来说:任意节点的根比左子树大,比右子树小,O(log2(n))
2. 节点
private class Node{
//维护的键值对,应该用泛型的,这里为了方便你懂的
public int key;
public int value;
//左右节点
public Node left;
public Node right;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
}
3. 遍历
public void preOrder(){
preOrder(root);
}
/**
* @param node 根据该节点往下遍历
*/
private void preOrder(Node node){
if(node != null){
System.out.println(node.value);
preOrder(node.left);
preOrder(node.right);
}
}
4. 查找
最先判断节点是否为空,再考虑大于小于,最后才考虑等于
public Node get(int key){
//最先判断节点是否为空,再考虑大于小于,最后才考虑等于
Node node = root;
while(node != null){
if(key > node.key){
node = node.right;
}else if(key < node.key){
node = node.left;
}else {
return node;
}
}
return null;
}
5. 插入
public void add(int key,int value){
Node node = root;
//树为空时,要初始化设置根结点
if(node == null){
root = new Node(key,value);
return ;
}
while(node != null){
//往右移
if(key > node.key){
//当右子树为空时,即插入
if(node.right == null){
node.right = new Node(key,value);
return ;
}else{
node = node.right;
}
//往左移
}else if(key < node.key){
if(node.left == null){
node.left = new Node(key,value);
return ;
}else{
node = node.left;
}
//相等替换
}else{
node.value = value;
return ;
}
}
}
6. 最值及节点
二叉查找树的最左节点为最小值,最右为最大值
public int max(){
Node node = max(root);
return node.value;
}
private Node max(Node node){
while(node.right != null){
node = node.right;
}
return node;
}
public int min(){
Node node = min(root);
return node.value;
}
private Node min(Node node){
while(node.left != null){
node = node.left;
}
return node;
}
/**
* 删除最小节点
*/
private Node DelMin(Node node){
if(node.left == null){
return node.right;
}
node.left = DelMin(node.left);
return node;
}
7. 删除
删除节点分三种情况
- 被删节点没有子树(直接删除)
- 被删节点只有一个子树(孩子节点替换父节点)
- 被删节点有左右子树(看图)
public Node delete(int key){
return delete(root, key);
}
private Node delete(Node node,int key){
if(key > node.key){
node.right = delete(node.right,key);
}else if(key < node.key){
node.left = delete(node.left,key);
}else{
//当被删节点不多于一个子树时
if(node.left == null){
return node.right;
}else if(node.right == null){
return node.left;
}else{
//被删节点有左右子树
//保存被删节点到临时变量
Node temp = node;
//找到被删节点的右子树中最小的节点,替换原来的节点
node = min(temp.right);
//看图更易理解
node.right = DelMin(temp.right);
//搞定左子树
node.left = temp.left;
}
}
return node;
}
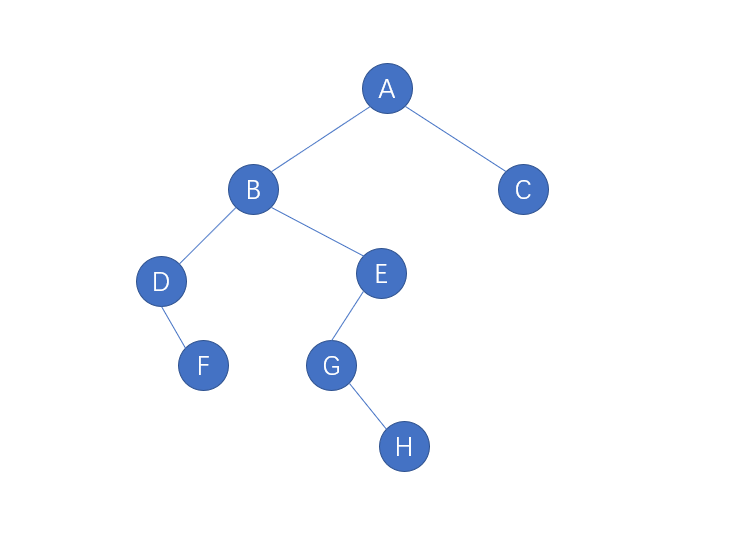
假如B为被删节点,步骤:
- 保存被删节点B到临时变量temp
- 用B右子树的最小节点G来替换B
- 用G右子树来代替E左子树
- 把G的左子树代替为B的左子树
8. 整体代码
/**
* 二叉查找树的实现
* @author Howl
* @version 0.0.1
* @date 20/1/13
*/
public class BinarySearchTree {
//维护一个根结点,与遍历相关的功能都需用到
private Node root;
/**
* 内部节点类
* @author Howl
*/
private class Node{
//维护的键值对,应该用泛型的,这里为了方便你懂的
public int key;
public int value;
//左右节点
public Node left;
public Node right;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
}
/**
* 先序遍历
*/
public void preOrder(){
preOrder(root);
}
/**
* @param node 根据该节点往下遍历
*/
private void preOrder(Node node){
if(node != null){
System.out.println(node.value);
preOrder(node.left);
preOrder(node.right);
}
}
/**
* @param key 根据key来查找
* @return 返回key对应的节点,没有就返回null
*/
public Node get(int key){
//最先判断节点是否为空,再考虑大于小于,最后才考虑等于
Node node = root;
while(node != null){
if(key > node.key){
node = node.right;
}else if(key < node.key){
node = node.left;
}else {
return node;
}
}
return null;
}
/**
* 添加节点
* @param key 键
* @param value 值
* @return
*/
public void add(int key,int value){
Node node = root;
//树为空时,要初始化设置根结点
if(node == null){
root = new Node(key,value);
return ;
}
while(node != null){
//往右移
if(key > node.key){
if(node.right == null){
node.right = new Node(key,value);
return ;
}else{
node = node.right;
}
//往左移
}else if(key < node.key){
if(node.left == null){
node.left = new Node(key,value);
return ;
}else{
node = node.left;
}
//相等替换
}else{
node.value = value;
return ;
}
}
}
/**
* 查找最值
* @return 最值
*/
public int max(){
Node node = max(root);
return node.value;
}
/**
* 查找最值的节点
* @param node 从该节点开始查找
* @return 返回最值对应的节点
*/
private Node max(Node node){
while(node.right != null){
node = node.right;
}
return node;
}
public int min(){
Node node = min(root);
return node.value;
}
private Node min(Node node){
while(node.left != null){
node = node.left;
}
return node;
}
/**
* 删除最小节点
*/
private Node DelMin(Node node){
if(node.left == null){
return node.right;
}
node.left = DelMin(node.left);
return node;
}
/**
* 删除节点
* @param key 根据key来删除
* @return 被删除的节点
*/
public Node delete(int key){
return delete(root, key);
}
private Node delete(Node node,int key){
if(key > node.key){
node.right = delete(node.right,key);
}else if(key < node.key){
node.left = delete(node.left,key);
}else{
//找到需要删的节点
if(node.left == null){
return node.right;
}else if(node.right == null){
return node.left;
}else{
Node temp = node;
//找到右子树最小的节点,替换原来的节点
node = min(temp.right);
//
node.right = DelMin(temp.right);
//搞定左子树
node.left = temp.left;
}
}
return node;
}
}
9. 测试
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
int[] arrs = {12,10,13,8,11,7,9};
for (int arr : arrs){
bst.add(arr, arr);
}
bst.delete(8);
bst.delete(13);
bst.preOrder();
}
12
10
9
7
11




 浙公网安备 33010602011771号
浙公网安备 33010602011771号



