LeetCode Notes_#450_删除二叉搜索树中的节点
LeetCode Notes_#450_删除二叉搜索树中的节点
Contents
题目
给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。
一般来说，删除节点可分为两个步骤：
- 首先找到需要删除的节点；
- 如果找到了，删除它。
说明： 要求算法时间复杂度为 O(h)，h 为树的高度。
示例:
root = [5,3,6,2,4,null,7]
key = 3
5
/ \
3 6
/ \ \
2 4 7
给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
5
/ \
4 6
/ \
2 7
另一个正确答案是 [5,2,6,null,4,null,7]。
5
/ \
2 6
\ \
4 7思路分析
BST的删除操作是BST数据结构最难的一个操作，更详细的讲解可以参考 《算法第四版》3.2.3.5小节。
主要分为两步：
1. 找到待删除节点
不能把搜索和删除两步操作分离，因为删除节点后，还要把新的子树连接到父节点。这个操作只能通过递归的回溯来进行。
if(key < root.val){
//因为key节点在左子树当中，所以就缩小范围，在左子树当中删除key节点
root.left = deleteNode(root.left, key);
//递归调用结束，把删除后的子树连接到root上面
return root;
}
else if(key > root.val){
//同理，右子树的情况
root.right = deleteNode(root.right, key);
return root;
}2. 删除待删除节点
删除操作需要分情况考虑，有如下的三种情况：
1. 待删除节点没有子节点，可以直接将其删除
2. 待删除节点只有一个子节点，用它的子节点代替它
3. 待删除节点有两个子节点，则需要用待删除节点在中序遍历中的前驱或者后继代替它
- 前驱节点一定是左子树的最大节点（也就是左子树最右下角的节点）
- 后继节点一定是右子树的最小节点（也就是右子树最左下角的节点）
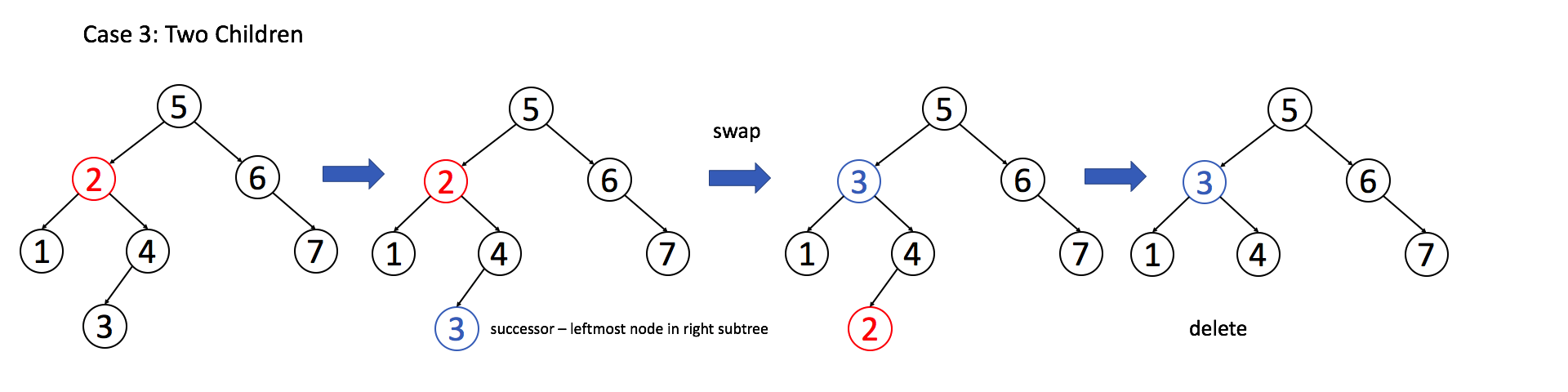
总结来说，BST在删除节点之前，中序遍历有序。删除节点之后，中序遍历应该还是有序的。
解答
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null) return null;
if(key < root.val){
//因为key节点在左子树当中，所以就缩小范围，在左子树当中删除key节点
root.left = deleteNode(root.left, key);
//递归调用结束，把删除后的子树连接到root上面
return root;
}
else if(key > root.val){
//同理，右子树的情况
root.right = deleteNode(root.right, key);
return root;
}
//key == root.val,即遇到的root刚好就是待删除的节点
else{
//左子树为null,用右子树替代key节点(左右子树同时为null,也正确)
if(root.left == null) return root.right;
////右子树为null,用左子树替代key节点
else if(root.right == null) return root.left;
else{
//后继节点其实就是右子树里的最小值
TreeNode successor = min(root.right);
//在右子树当中需要删除successor,因为successor要和key交换位置
successor.right = deleteMin(root.right);
//左子树没有变化
successor.left = root.left;
return successor;
}
}
}
//找到BST当中的最小节点，返回这个节点
private TreeNode min(TreeNode node){
if(node.left == null) return node;
return min(node.left);
}
//删除BST当中的最小节点，返回删除之后的树的根节点
private TreeNode deleteMin(TreeNode node){
//找到最小节点，没有左孩子，用它的右子树代替它
if(node.left == null) return node.right;
node.left = deleteMin(node.left);
return node;
}
}复杂度分析
时间复杂度：O(h)
空间复杂度：O(1)
