剑指Offer_#59-I_滑动窗口的最大值(LeetCode#239)
剑指Offer_#59-I_滑动窗口的最大值(LeetCode#239)
Contents
题目
给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7提示：
你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的大小。
方法1：双端队列
用一个双端队列维护窗口的最大值，保证双端队列是非严格递减的（前一个元素大于等于后一个元素），那么双端队列的第一个元素正好就是当前窗口当中的最大值。
算法流程
遍历数组，维护两个指针i,j，分别指向窗口左右边界，右指针从第一个元素开始，左指针则始终与右指针相距k-1(中间刚好有k个元素)，指针每次移动后执行如下过程：
- i>0时(在此之前窗口还未形成），如果当前队列的头部恰好是nums[i-1]，则将其从队列里删除
- 比较nums[j]与队列当中的数字(从后往前看)，将小于nums[j]的全部删除（因为nums[j]是当前新加入的数字，比它小的绝不可能是窗口最大值）
- 将nums[j]加入到队列尾部，这时整个队列是非严格递减的，头部的值就是当前窗口的最大值
- 如果i >= 0,将头部数字加入到res中
总结起来，就是维护一个特殊的双端队列数据结构，窗口滑动时，将上个窗口的第一个元素删除，再把上个窗口之后的第一个元素加入进来，且保证队列头部数字最大。
细节问题：
- 指针初始值：
j = 0,i = 0-(k - 1) = 1-k - 结果数组res的长度：从第k个元素开始，到第n个元素，有几个数字？n-k+1
- java的双端队列：
Deque<Integer> deque = new LinkedList<>();- peekFirst(),peekLast()
- removeFirst(),removeLast()
- addLast
- 特殊情况：空数组，k = 0,返回空数组
- 删除元素的时候，必须保证队列非空
解答1:双端队列
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
if(n == 0 || k == 0) return new int[0];
Deque<Integer> deque = new LinkedList<>();
//res的长度就是滑动窗口的个数，共有n-k+1个
int[] res = new int[n - k + 1];
//ERROR:不可以写成 int i = 1 - k,int j = 0; 因为这样写是两个statement
for(int i = 1 - k,j = 0; j <= n - 1; i++, j++){
//1.如果当前窗口删除掉的nums[i - 1]恰好时上一个窗口的最大值，在队列中将这个元素删除
if(i >= 1 && deque.peekFirst() == nums[i - 1])
deque.removeFirst();
//2.当前窗口新加入nums[j]，小于此值的绝对不会是最大值，所以直接从队列将这些较小的数字删除（从后往前）
//ERROR:这里判断非空要写在前，利用短路特性
while(!deque.isEmpty() && nums[j] > deque.peekLast())
deque.removeLast();
//3.将新加入的nums[j]加入队列末尾
deque.addLast(nums[j]);
//4.当前窗口最大值就是队列头部，将其写入res
if(i >= 0) res[i] = deque.peekFirst();
}
return res;
}
}复杂度分析
时间复杂度：O(n),遍历整个数组
空间复杂度：O(k),因为双端队列里边的数字始终就是当前窗口的数字，所以队列的大小是k
方法2：大根堆（优先队列）
严格维护滑动窗口
模拟窗口滑动过程，每次滑动的时候，移除上一次的左边界值，新增右边界值。但是在nums为大数据输入的时候，会出现超时的情况，原因应该是因为remove()函数调用过多，这个方法的复杂度是O(logn)。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
PriorityQueue<Integer> pq = new PriorityQueue<>((Integer x, Integer y) -> (y - x));
int[] res = new int[nums.length - k + 1];
for(int m = 0; m <= k - 1; m++) pq.offer(nums[m]);
res[0] = pq.peek();
for(int m = 1, n = k; n <= nums.length - 1; m++, n++){
pq.remove(nums[m - 1]);
pq.offer(nums[n]);
res[m] = pq.peek();
}
return res;
}
}
优化的代码（避免使用remove()）
核心在于堆当中不仅要记录元素的数值，还要记录元素在数组当中的索引，然后就可以判断出来堆顶元素是不是窗口内的，如果不是，那就可以把他弹出，直到遇到窗口内的最大元素。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
//大顶堆，首先按照数值排序，数值相同的情况下按照索引大小排序
PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>(){
public int compare(int[] pair1, int[] pair2){
return pair2[0] - pair1[0] != 0 ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
}
});
//初始化大顶堆，放入第一个窗口内的元素，即[0...k-1]
for(int i = 0; i <= k - 1; i++) pq.offer(new int[]{nums[i], i});
int[] res = new int[nums.length - k + 1];
res[0] = pq.peek()[0];
//滑动窗口，求出每个窗口的最大值
for(int i = k; i <= nums.length - 1; i++){
pq.offer(new int[]{nums[i], i});
//将所有不在窗口范围内的数值都删除
while(pq.peek()[1] < i - k + 1) pq.poll();
//此时的堆顶元素必然是窗口内最大数值
res[i - k + 1] = pq.peek()[0];
}
return res;
}
}复杂度分析
时间复杂度：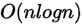
,每次将一个元素放入堆，复杂度是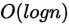
空间复杂度：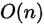
,最坏情况（严格递增数组），会把所有的元素都加入堆中而不会弹出
方法3：分块求前缀最大值及后缀最大值
参考滑动窗口最大值 - 滑动窗口最大值 - 力扣（LeetCode）中的方法3。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int[] res = new int[nums.length - k + 1];
int[] suffix_max = new int[nums.length];
int[] prefix_max = new int[nums.length];
//填充前缀最大值
for(int i = 0; i < nums.length; i++){
//如果刚好是一个k分块的开头，那么最大值就是nums[i]
if(i % k == 0){
prefix_max[i] = nums[i];
}else{
prefix_max[i] = Math.max(nums[i], prefix_max[i - 1]);
}
}
//填充后缀最大值
for(int i = nums.length - 1; i >= 0; i--){
if(i == nums.length - 1 || (i + 1) % k == 0){
suffix_max[i] = nums[i];
}else{
suffix_max[i] = Math.max(nums[i], suffix_max[i + 1]);
}
}
//计算结果
for(int i = 0; i < res.length; i++){
res[i] = Math.max(suffix_max[i], prefix_max[i + k - 1]);
}
return res;
}
}复杂度分析
时间复杂度：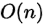
，两轮遍历，第三轮计算结果
空间复杂度：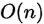
，使用了前缀最大值和后缀最大值数组
