剑指Offer_#40_最小的k个数
剑指Offer_#40_最小的k个数
Contents
题目
输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。
示例 1：
输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]示例 2：
输入：arr = [0,1,2,1], k = 1
输出：[0]
限制：
0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000思路分析
方法1：利用快排中的切分partition()函数
快排当中的partition函数，可以基于数组中某个元素v作为标准，将比v小的元素放到v的前面，将比v大的元素放到v的后面。我们可以不断调用这个函数，缩小切分范围，直到v元素的索引刚好是k-1。此时数组的前k项就是结果。
与快排不同的是，快排的出口条件是hi = lo + 1，即需要不断缩小范围，直到指针相邻，最终整个数组都是有序的。
在本题中，返回的数组不需要是有序的，所以跟快排有所不同。
关于快排及partition函数，参考《算法第四版》2.3节。
方法2：大根堆辅助（可用Java中的PriorityQueue实现）
用一个数据容器来保存最小的k个数字，最合适的是大根堆，每次可以自动弹出最大值。Java中的PriorityQueue可以实现。
在堆的元素个数小于k时，按顺序将数组里数字压入。
堆的元素超过k时，如果数组里的数字小于堆里最大值，替换掉堆里的最大值。
解答
解法1：利用快排中的切分partition()函数
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(arr.length == 0 || k == 0) return new int[0];
int start = 0;
int end = arr.length - 1;
int index = partition(arr, start, end);
while(index != k - 1){
if(index > k - 1){
end = index - 1;
index = partition(arr, start, end);
}
else{
start = index + 1;
index = partition(arr, start, end);
}
}
//返回nums数组的前k个元素
return Arrays.copyOf(arr, k);
}
int partition(int[] nums,int lo,int hi){
int v = nums[lo];
//左右扫描指针
//i不需要初始化为lo-1,因为第一个nums[lo]是k,不需要扫描这个元素
int i = lo,j = hi + 1;
while(true){
//错误写法:当k == nums.length时，会导致数组越界
//while(nums[++i] < v) if(i == hi) break;
//while(nums[--j] > v) if(j == lo) break;
//i从lo + 1开始向后扫描，直到遇到 大于等于v的数字，指针i停留在此
while(++i <= hi && nums[i] < v);
//j从hi开始向前扫描，直到遇到 小于等于v的数字，指针j停留在此
while(--j >= lo && nums[j] > v);
//i > j的情况，已经切分好左右子数组，不可以再交换了
//i = j的情况，无需交换
if(i >= j) break;
exch(nums, i, j);
}
exch(nums, lo, j);//将v放入正确的位置
return j;
}
//数组nums作为形参，属于引用传递，所以函数运行后可以改变实参
void exch(int[] nums, int idxA, int idxB){
int tmp = nums[idxA];
nums[idxA] = nums[idxB];
nums[idxB] = tmp;
}
}复杂度分析
时间复杂度：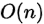
,因为每次遍历的范围可以看作上次的一半，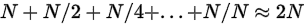
空间复杂度：不需要借助额外变量，但是改变了数组
解法2：大根堆辅助（可用Java中的PriorityQueue实现）
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(k == 0 || arr.length == 0) return new int[0];
//使用lambda表达式重载了PriorityQueue当中的compare方法
Queue<Integer> pq = new PriorityQueue<>((v1,v2) -> v2-v1);
//因为这里不修改数组元素，所以可以采用foreach循环
for(int num:arr){
if(pq.size() < k) pq.offer(num);
else if(num < pq.peek()){
pq.poll();
pq.offer(num);
}
}
//遍历pq取出所有元素到res数组
int[] res = new int[k];
int idx = 0;
for(int num:pq){
res[idx++] = num;
}
return res;
}
}用lambda表达式可以重载PriorityQueue中的compare方法。以下是一些相关的参考文章。
lambda表达式
PriorityQueue
复杂度分析
时间复杂度：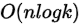
空间复杂度：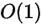
,只使用了大小为k的优先队列
