蓝桥杯必备算法模板
1.输入
推荐使用这种的输入,读取的数据量大的时候,速度更快。
static class InputReader { private BufferedReader bf = null; private StringTokenizer stz = null; public InputReader() { bf = new BufferedReader(new InputStreamReader(System.in),32*1024); } public boolean hasNext() { while(stz == null || !stz.hasMoreTokens()) { try { stz = new StringTokenizer(bf.readLine()); } catch (IOException e) { return false; } } return true; } public String next() { if(hasNext()) { return stz.nextToken(); } return null; } public int nextInt() { return Integer.parseInt(next()); } public double nextDouble() { return Double.parseDouble(next()); } }
2.进制转换
十进制转换成n进制
InputReader sc = new InputReader(); int num = sc.nextInt(); System.out.println(Integer.toString(num, 16));//这里是转成16进制
n进制转换成十进制
InputReader sc = new InputReader(); String str = sc.next(); System.out.println(Integer.valueOf(str, 16));//这里代表字符串使用16进制表示的
以上处理的进制问题没有考虑溢出问题。也就是某个进制代表的数字很大,int类型不足以表示
n进制转换十进制(推荐)
InputReader sc = new InputReader(); String str = sc.next(); BigInteger bigInteger = new BigInteger(str, 16); System.out.println(bigInteger);
3. 日期运算(Calendar的API使用)
真题:世纪末的星期
1999年的12月31日是星期五,请问:未来哪一个离我们最近的一个世纪末年(即xx99年)的12月31日正好是星期天(即星期日)?
请回答该年份(只写这个4位整数,不要写12月31等多余信息)。
public static void main(String[] args) { Calendar calendar = Calendar.getInstance(); for (int i = 1999; i < 10000; i+=100) { calendar.set(i, 11, 31);//月份从0开始计算 if(calendar.get(Calendar.DAY_OF_WEEK) == 1) { System.out.println(i); //2299 break; } } }
4.递归
递归就是思考解决问题的方向是自顶向下的
4.1. 最常用的递归就是全排列

public static void main(String[] args) { String[] arr = new String[] {"A","B","C"}; int n = arr.length; recursion(arr,0,n); } private static void recursion(String[] arr,int start,int end) { if(start == end) { print(arr); return; } for (int i = start; i < end; i++) { Utils.swap(arr, i, start); // Arrays.sort(arr,start+1,end); recursion(arr,start+1,end); Utils.swap(arr, start, i); } } private static void print(String[] arr) { for (int i = 0; i < arr.length; i++) { System.out.print(arr[i]); } System.out.println(); }
不带重复排列的全排列

public class Main { static int[] arr = {1,1,3,3}; static boolean[] vis = new boolean[arr.length]; static int[] res = new int[arr.length]; static HashSet<String> hashSet = new HashSet<String>(); public static void main(String[] args) { f(0); } private static void f(int cur) { String str = ""; if(cur == arr.length) { for(int i=0;i<arr.length;i++) { str += arr[i]; } if(!hashSet.contains(str)) { hashSet.add(str); System.out.println(str); } return; } for (int i = cur; i < arr.length; i++) { swap(i,cur); f(cur+1); swap(i,cur); } } private static void swap(int a,int b) { int t = arr[a]; arr[a] = arr[b]; arr[b] = t; } }
4.2. 递归转递推
4.3. DFS(搜索+检查)
标题: 振兴中华
小明参加了学校的趣味运动会,其中的一个项目是:跳格子。
地上画着一些格子,每个格子里写一个字,如下所示:(也可参见p1.jpg)
从我做起振
我做起振兴
做起振兴中
起振兴中华
比赛时,先站在左上角的写着“从”字的格子里,可以横向或纵向跳到相邻的格子里,但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。
要求跳过的路线刚好构成“从我做起振兴中华”这句话。
请你帮助小明算一算他一共有多少种可能的跳跃路线呢?
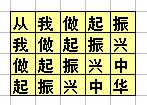
将“从我做起振兴中华”用数字0到7代替从0开始往下和往右深搜

static int[][] arr = { { 0, 1, 2, 3, 4 }, { 1, 2, 3, 4, 5 }, { 2, 3, 4, 5, 6 }, { 3, 4, 5, 6, 7 } }; static boolean[][] visited = new boolean[4][5]; public static void main(String[] args) { int ans = dfs(0,0,0); System.out.println(ans); //35 } /** * * @param x * @param y x ,y 是坐标 * @param cur 当前应该是第几个数字 */ private static int dfs(int x, int y,int cur) { int res = 0; visited[x][y] = true; if(cur == 7 && arr[x][y] == 7) { return 1; } if(inArea(x+1,y) && !visited[x+1][y]) { res+=dfs(x+1,y,cur+1); visited[x+1][y] = false;//回溯 } if(inArea(x,y+1)&& !visited[x][y+1]) { res+=dfs(x,y+1,cur+1); visited[x][y+1] = false;//回溯 } return res; } private static boolean inArea(int x, int y) { if(x>=0 && x < 4 && y>=0 && y < 5) { return true; } return false; }
当然这是最一般的解法,但是题目给的数据比较特殊,从左上到右下每一个位置,都可以往下或者右走,并且一定只能是这个顺序。于是可以这样写

public static void main(String[] args) { int ans = f(0,0); System.out.println(ans); //35 } private static int f(int x, int y) { int res = 0; if(x==3 && y== 4) { return 1; } if(x+1>=0 && x+1<=3) res+= f(x+1,y); if(y+1>=0 && y+1<=4) res+= f(x, y+1); return res; }
4.3 记忆型递归与博弈型问题
5.枚举,全排列暴力解法
标题1:六角填数
如图【1.png】所示六角形中,填入1~12的数字。
使得每条直线上的数字之和都相同。
图中,已经替你填好了3个数字,请你计算星号位置所代表的数字是多少?
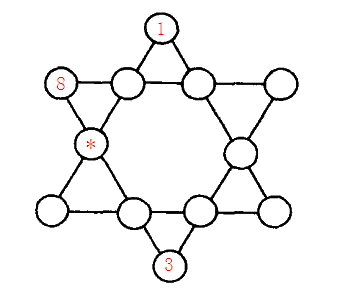
思路,按照从上到下,从左到右对还没有填入的数字进行编号,题目转换为求下标为3的那个数是多少

public static void main(String[] args) { int[] arr = {2,4,5,6,7,9,10,11,12}; f(arr,0);//全排列 } private static void f(int[] arr,int cur) { if(cur == arr.length) { check(arr); return; } for(int i=cur;i<arr.length;i++) { swap(arr,i,cur); f(arr,cur+1); swap(arr,i,cur); } } private static void check(int[] arr) { int r1 = 1 + arr[0]+arr[3]+arr[5]; int r2 = 1 + arr[1]+arr[4]+arr[8]; int r3 = 8 + arr[0]+arr[1]+arr[2]; int r4 = 11 + arr[6]+arr[3]; int r5 = 3 + arr[2]+arr[4]+arr[7]; int r6 = arr[5] + arr[6]+arr[7]+arr[8]; if(r1==r2&&r2==r3&&r3==r4&&r4==r5&&r5==r6) { for(int i=0;i<arr.length;i++) { System.out.print(arr[i]+" "); //9 2 7 10 12 6 5 4 11 所以答案为10 } } } private static void swap(int[] arr, int i, int cur) { int t = arr[i]; arr[i] = arr[cur]; arr[cur] = t; }
再举个例子
生日蜡烛
某君从某年开始每年都举办一次生日party,并且每次都要吹熄与年龄相同根数的蜡烛。
现在算起来,他一共吹熄了236根蜡烛。
请问,他从多少岁开始过生日party的?
请填写他开始过生日party的年龄数。

static int sum(int start, int end) { return (start+end) * (end - start +1) /2;//等差数列求和公式 } public static void main(String[] args) { for (int start = 1; start < 100; start++) { for (int end = start + 1; end < 100; end++) { if(sum(start,end) == 236) { System.out.println(start +" " +end);//26 33 所以答案就是26 } } } }
6.快速幂运算

public static int quickExp(int n,int m) { int res = 1; while(m > 0) { if((m&1)==1) { res *= n; } n = n*n; m = m>>1; } return res; }
7.矩阵运算
矩阵乘法运算

private static int[][] multiple(int[][] m1, int[][] m2) { int[][] res = new int[m1.length][m2[0].length]; for(int i=0;i<m1.length;i++) { for(int j=0;j<m2[i].length;j++) { for(int k=0;k<m2.length;k++) { res[i][j] += m1[i][k]* m2[k][j]; } } } return res; }
矩阵快速幂运算

private static int[][] quickExp(int[][] m, int n) { int[][] res = new int[N][N]; for(int i=0;i<N;i++) { for (int j = 0; j < N; j++) { if(i == j) res[i][j] = 1; else res[i][j] = 0; } } while(n>0) { if((n & 1) == 1) res = multiple(res, m); //调用的是上面的矩阵乘法公式 m = multiple(m, m); n = n>>1; } return res; }
应用:快速求斐波那契数O(logn)的时间复杂度。(在最后会提到)
8.贪心
8.动态规划(dp)(*****)
前面讲过递归就是思考解决问题的方向是自顶向下的,而动态规划是恰恰相反。
不过,通常在解决问题的时候,我们应该先要自顶向下的思考,因为自顶向下思考问题,比较简单。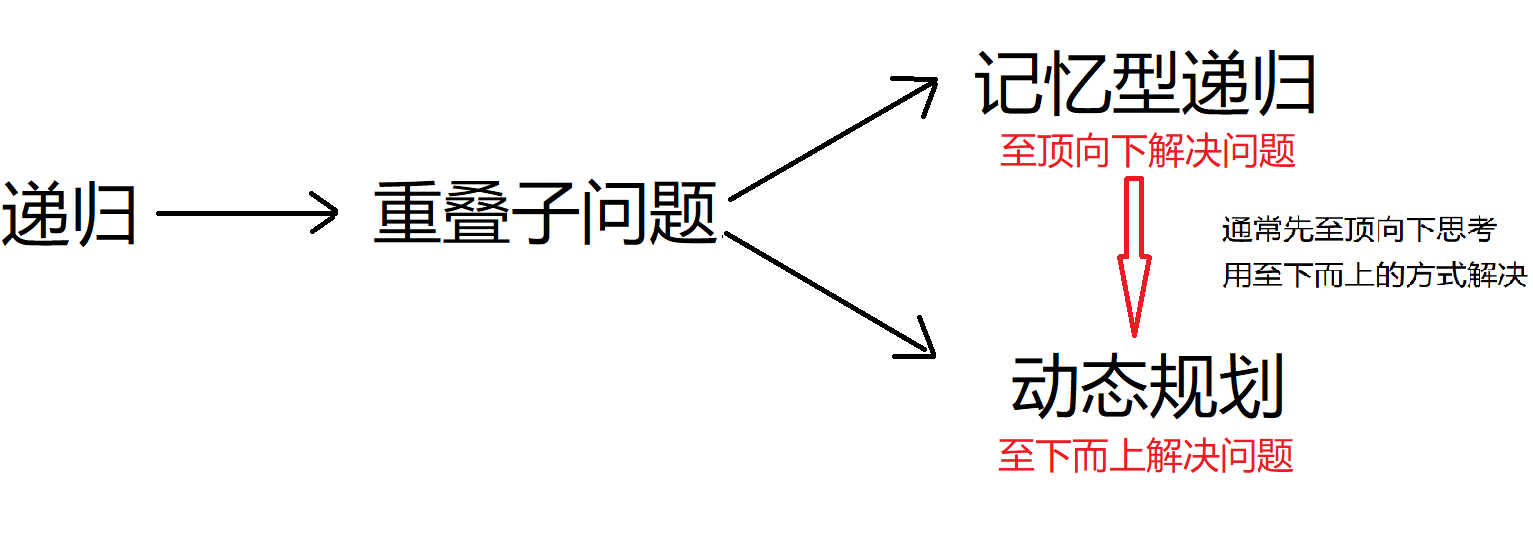
从最简单的dp开始

class Solution { private int[] memo; public int climbStairs(int n) { if (n == 1) return 1; if (n == 2) return 2; memo = new int[n + 1]; memo[1] = 1; memo[2] = 2; for (int i = 3; i < n + 1; i++) { memo[i] = memo[i - 1] + memo[i - 2]; } return memo[n]; } }
如果感觉没问题的话,可以练习下面两道题:
例2:整数拆分
2.1 简单递归解法
分析: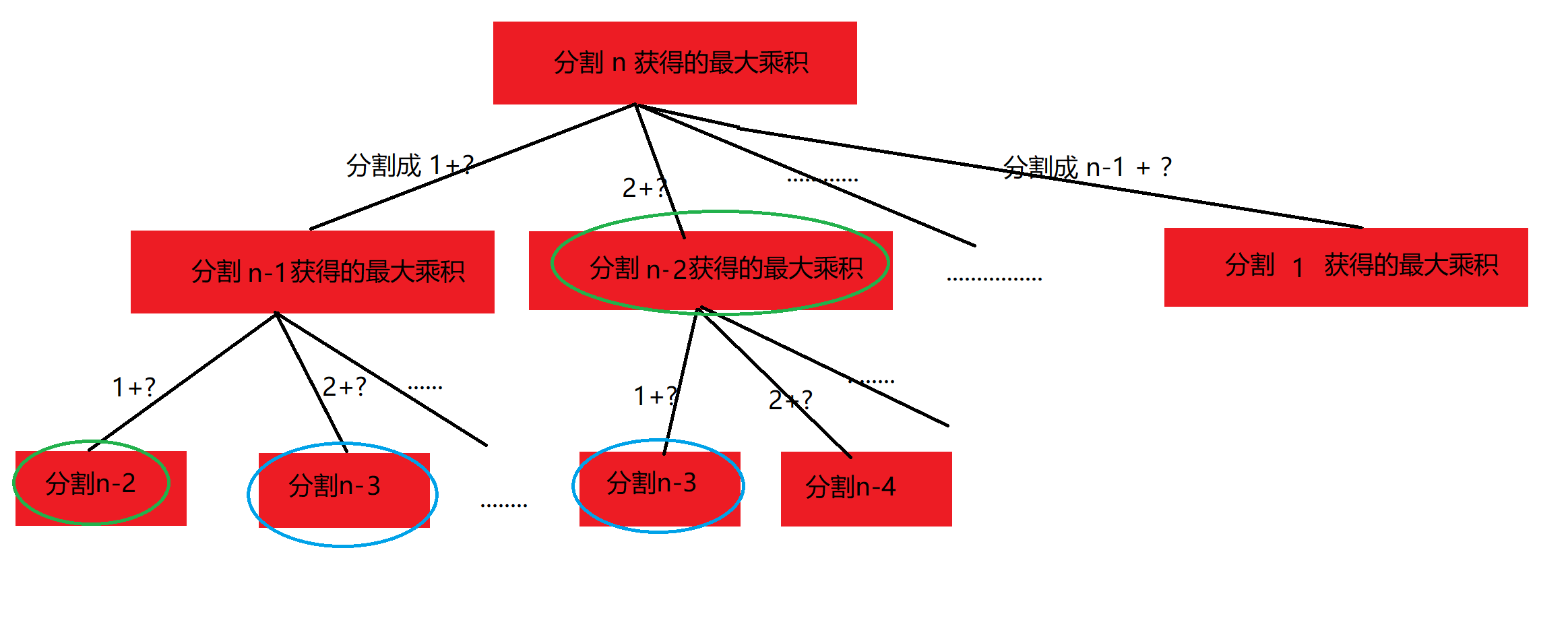

class Solution { public int integerBreak(int n) { return breakInteger(n); } //计算n的拆分乘积最大值,注意:一定会将n至少分成两部分 private int breakInteger(int n) { if (n == 1) return 1; int res = 0; for (int i = 1; i < n; i++) { res = max3(res,i * (n-i),i * breakInteger(n - i)); } return res; } private int max3(int a, int b, int c) { return Math.max(Math.max(a, b), c); } // public static void main(String[] args) { // System.out.println(new Solution().integerBreak(4)); //} }
得到结果:

2.2 记忆型递归
记忆型递归的技巧,在每个求出结果的地方记录,在递归之前查询。

class Solution { private int[] memo; //memeo[i]代表第i个的拆分最大乘积 public int integerBreak(int n) { memo = new int[n+1]; return breakInteger(n); } //计算n的拆分乘积最大值,注意:一定会将n至少分成两部分 private int breakInteger(int n) { if (n == 1) return 1; if(memo[n]!=0) return memo[n]; int res = 0; for (int i = 1; i < n; i++) { res = max3(res,i * (n-i),i * breakInteger(n - i)); } memo[n] = res; return res; } private int max3(int a, int b, int c) { return Math.max(Math.max(a, b), c); } //public static void main(String[] args) { // System.out.println(new Solution().integerBreak(10)); // } }
2.3 动态规划(自底向上)

class Solution { public int integerBreak(int n) { int[] dp = new int[n + 1]; dp[1] = 1; for (int i = 2; i < n + 1; i++) { for (int j = 1; j <= i-1; j++) { dp[i] = max3(dp[i], j * (i - j), j * dp[i-j]); } } return dp[n]; } private int max3(int a, int b, int c) { return Math.max(Math.max(a, b), c); } public static void main(String[] args) { System.out.println(new Solution().integerBreak(5)); } }
leetcode练习:
例3:打家劫舍
3.1 递归写法(自下而上)
状态的定义:考虑偷取[ x ..... n-1]范围的房子 。通常把对状态的定义也叫做函数的定义

class Solution { public int rob(int[] nums) { return tryRob(nums, 0); } private int tryRob(int[] nums, int start) {//start代表从哪个位置开始 if(start >= nums.length){ return 0; } int res = 0; // res = Math.max(tryRob(nums, start + 1), nums[i] + tryRob(nums, i + 2)); // 这也是一种递归写法。 for (int i = start; i < nums.length; i++) { res = Math.max(res, nums[i] + tryRob(nums, i + 2)); } return res; } }
3.2 记忆型递归

class Solution { private int[] memo; public int rob(int[] nums) { memo = new int[nums.length]; return tryRob(nums, 0); } private int tryRob(int[] nums, int start) {//start代表从哪个位置开始 if(start >= nums.length){ return 0; } //开始前查询 if(memo[start]!=0) return memo[start]; int res = 0; for (int i = start; i < nums.length; i++) { res = Math.max(res, nums[i] + tryRob(nums, i + 2)); } //返回结果前记录 memo[start] = res; return res; } }
3.3 动态规划(自顶向下)

class Solution { private int[] dp;//dp[index] 代表从index的位置开始到最后一间房抢到的价值最大值 private int n; public int rob(int[] nums) { this.n = nums.length; if(nums.length == 0) return 0; dp = new int[n]; dp[n - 1] = nums[n - 1];//只有一个房间,那就抢。不用考虑------最基本问题 //考虑从i开始抢到的价值最大值 for (int i = n - 2; i >= 0; i--) { for (int j = i; j < n; j++) dp[i] = Math.max(dp[i], ((j + 2) < n ? dp[j + 2] : 0 ) + nums[j]);//一定要用已知的结果 } return dp[0]; } }
状态的定义02:考虑偷取[ 0 .... x ]范围里的房子 。
3.1 递归写法

class Solution { public int rob(int[] nums) { if (nums.length == 0) return 0; return tryRob02(nums, nums.length - 1); } private int tryRob02(int[] nums, int end) { if (end < 0) { return 0; } int res = 0; for (int i = end; i >= 0; i--) {//这里对[end....0]的每一个尝试偷取 res = Math.max(res, nums[i] + tryRob02(nums, i - 2));//从[end...0]这多个分支中取得最大值 } return res; } public static void main(String[] args) { long start = System.currentTimeMillis(); int[] nums = {2,7,9,3,1}; System.out.println(new Solution().rob(nums)); long end = System.currentTimeMillis(); System.out.println(end - start + "ms"); } }
3.2 记忆型递归

class Solution { private int[] memo; public int rob(int[] nums) { if (nums.length == 0) return 0; memo = new int[nums.length]; return tryRob02(nums, nums.length - 1); } private int tryRob02(int[] nums, int end) { if (end < 0) { return 0; } //递归前查询 if (memo[end] != 0) return memo[end]; int res = 0; for (int i = end; i >= 0; i--) {//这里对[end....0]的每一个尝试偷取 res = Math.max(res, nums[i] + tryRob02(nums, i - 2));//从[end...0]这多个分支中取得最大值 } //返回结果前记录 memo[end] = res; return res; } }
3.3 动态规划

class Solution { private int[] dp;//dp[index] 表示从0~index范围偷取的最大值 private int n; public int rob(int[] nums) { if (nums.length == 0) return 0; this.n = nums.length; dp = new int[n]; //找到最基本的问题的解 dp[0] = nums[0]; //由已知解逐步递推 for (int i = 1; i < n; i++) { for (int j = i; j >= 0; j--) { dp[i] = Math.max(dp[i], nums[j] + (j - 2 >= 0 ? dp[j - 2] : 0)); } } return dp[n-1]; } }
4. 01背包问题
4.1递归解法

import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.StringTokenizer; /** * 01背包的状态方程 F(n,c) n代表前n个物品,c代表背包容量 * F(i,c) = max( F(i-1,c) , v[i] + F(i,c-v[i]) ) */ public class Main { /** * @param w 重量 * @param v 价值 * @param c 背包容量 * @return */ public static int knapsack01(int[] w, int[] v, int c) { return bestValue(w, v, 0, c); } private static int bestValue(int[] w, int[] v, int index, int c) { if (index >= w.length || c <= 0) return 0; int res = bestValue(w, v, index + 1, c); if (c > w[index]) res = Math.max(res, v[index] + bestValue(w, v, index + 1, c - w[index])); return res; } public static void main(String[] args) { InputReader sc = new InputReader(); int n = sc.nextInt(); int c = sc.nextInt(); int[] v = new int[n]; int[] w = new int[n]; for (int i = 0; i < n; i++) { w[i] = sc.nextInt(); v[i] = sc.nextInt(); } System.out.println(knapsack01(w, v, c)); } /* * 下面就是输入类,之前介绍过了。可以不用在意 */ static class InputReader { private BufferedReader bf; private StringTokenizer stz; public InputReader() { bf = new BufferedReader(new InputStreamReader(System.in), 32 * 1014); stz = null; } public boolean hasNext() { while (stz == null || !stz.hasMoreTokens()) { try { stz = new StringTokenizer(bf.readLine()); } catch (IOException e) { return false; } } return true; } public String next() { if (hasNext()) return stz.nextToken(); return null; } public int nextInt() { return Integer.parseInt(next()); } } }
4.2 记忆型递归(核心代码)
注意memo的开辟空间

private int bestValue(int[] w, int[] v, int index, int c) { if (index > w.length || c <= 0) return 0; //递归前查询 if(memo[index][c] != 0) return memo[index][c]; int res = bestValue(w, v, index + 1, c); if (c > w[index]) res = Math.max(res, v[index] + bestValue(w, v, index + 1, c - w[index])); //返回前记录 memo[index][c] = res; return res; }
4.3 动态规划(核心)

private int[][] dp; //dp[index][c]代表 背包容量剩余c和可选[0,index]物品的价值最大值 private int n; /** * @param w 重量 * @param v 价值 * @param c 背包容量 * @return */ public int knapsack01(int[] w, int[] v, int c) { dp = new int[w.length][c + 1]; n = w.length; return bestValue(w, v, 0, c); } private int bestValue(int[] w, int[] v, int index, int c) { if (c <= 0 || w.length == 0) return 0; //初始化基本问题-------只有0 ~ 0(只有0)之间的物品可选 for (int capacity = 0; capacity <= c; capacity++) { if (capacity >= w[0]) dp[0][capacity] = v[0]; else dp[0][capacity] = 0; } //有基本问题推出一般问题 for (int i = 1; i < n; i++) { for (int cap = 0; cap <= c; cap++) { if(cap >= w[i]) dp[i][cap] = Math.max(dp[i-1][cap],v[i] + dp[i-1][cap - w[i]]); else dp[i][cap] = dp[i-1][cap]; } } return dp[n-1][c]; }
例5:leetcode 416 基于01背包的问题
详细见代码注释

class Solution { /** * 状态定义:F(i,C) i代表0~i的可选范围,C代表填充的背包容量(在这里背包的容量就是sum/2) * 方程的含义是:在0~i的范围里能否填充C * 状态转移方程F(i,C) --> F(i-1,C) || F(i,C-nums[i]) */ public boolean canPartition(int[] nums) { if (nums.length < 0) return false; int n = nums.length; int C = 0; for (int i = 0; i < n; i++) C += nums[i]; if (C % 2 != 0) return false; C = C / 2; boolean[] dp = new boolean[C + 1]; //找到基本问题的解 for (int i = 0; i <= C; i++) { dp[i] = (nums[0] == i);//只用第1(从0到0 [0])个数字去试试能不能填满背包 } //试试用[0...i]的范围,一步一步推导 for (int i = 1; i < n; i++) { for (int j = C; j >= nums[i]; j--) { dp[j] = dp[j] || dp[j - nums[i]]; } } return dp[C]; } }
练习:兑换硬币
典例6:最长上升子序列(LIS)
分析在代码中已体现

class Solution { /** * 状态的定义:LIS(i) 一定以i结尾的最长递增子序列 * 状态的转移:LIS(i) --> 1 + LIS(j | if(nums[j] < nums[i]) ) */ private int n; public int lengthOfLIS(int[] nums) { this.n = nums.length; if(nums.length == 0) return 0; int[] dp = new int[n]; //找到基本问题的解 for (int i = 0; i < n; i++) dp[i] = 1; //根据状态转移方程推导更进一步问题的解 for (int i = 1; i < n; i++) { for (int j = 0; j < i; j++) { if(nums[j] < nums[i] && dp[i] < 1 + dp[j] ){ dp[i] = 1 + dp[j]; } } } //一定要注意返回的是dp数组中的最大值 不是直接return dp[n]. int res = 0; for (int i = 0; i < n; i++) { res = Math.max(res,dp[i]); } return res; } public static void main(String[] args) { System.out.println(new Solution().lengthOfLIS(new int[]{1,3,6,7,9,4,10,5,6})); } }
如果进一步求出这个子序列是什么呢?
练习:摆动序列
更多的问题:
状态的定义: LCS(m , n) 代表 s1[0....m] 和 s2[0.....n]的最长公共子序列的长度
状态转移方程:
分为两种情况:
如果s1[m] == s2[n]
LCS(m,n) = 1 + LCS ( m-1 , n-1)
如果s1[m] != s2[n]
LCS(m , n ) = max(LCS(m-1,n) , LCS( m , n-1 ) )

class Solution { /** * 状态定义: LCS(m , n) 代表 s1[0....m] 和 s2[0.....n]的最长公共子序列的长度 * 状态转移方程: * 如果s1[m] == s2[n] * LCS(m,n) = 1 + LCS ( m-1 , n-1) * 如果s1[m] != s2[n] * LCS(m , n ) = max(LCS(m-1,n) , LCS( m , n-1 ) ) */ private String s1; private String s2; public int longestCommonSubsequence(String text1, String text2) { this.s1 = text1; this.s2 = text2; return LCS(s1.length() - 1, s2.length() - 1); } private int LCS(int m, int n) { //找到一般问题的解 int[][] dp = new int[n + 1][m + 1];//dp[i][j]的含义是:s1[0..i]与s2[0..j]的最长公共子序列 boolean flag = false; for (int i = 0; i <= m; i++) if (!flag && s2.charAt(0) == s1.charAt(i)) { dp[0][i] = 1; flag = true; }else if(flag){ dp[0][i] = 1; } //根据状态转移方程推出更进一步的问题的解 for (int i = 1; i <= n; i++) { for (int j = 0; j <= m; j++) { if (s2.charAt(i) == s1.charAt(j)) if( i-1 >=0 && j-1>=0) dp[i][j] = 1 + dp[i - 1][j - 1]; //这里与递归是一样的意义 else dp[i][j] = 1; else dp[i][j] = Math.max((i-1>=0?dp[i - 1][j]:0), (j-1>=0?dp[i][j - 1]:0));//这里与递归是一样的意义 } } return dp[n][m]; } public static void main(String[] args) { System.out.println(new Solution().longestCommonSubsequence("bl", "yby")); } }
9.树
线段树/区间数

/** * 该接口是为了为了使线段树更通用。 * 当要求一段区间的和 ,merge的功能是 求 a+b * 当要求一段区间的积 ,merge的功能是 求 a*b * 也就是对于不同的业务,不需要重新修改SegmentTree的代码 * @author zhanyuhao * @version 创建时间:2020年3月3日 下午9:57:45 * 类说明 */ public interface Merger<E> { E merge(E a,E b); }

/** * 线段树(区间树) * * @author zhanyuhao * @version 创建时间:2020年3月3日 下午7:55:54 类说明 */ public class SegmentTree<E> { private E[] data; private E[] tree; private Merger<E> merger; public SegmentTree(E[] arr, Merger<E> merger) { this.merger = merger; data = (E[]) new Object[arr.length]; tree = (E[]) new Object[4 * arr.length]; for (int i = 0; i < arr.length; i++) data[i] = arr[i]; buildTree(0, 0, data.length - 1); } private void buildTree(int treeIndex, int l, int r) { if (l == r) { tree[treeIndex] = data[l]; return; } int mid = l + (r - l) / 2; int leftIndex = leftChild(treeIndex); int rightIndex = rightChild(treeIndex); buildTree(leftIndex, l, mid); buildTree(rightIndex, mid + 1, r); tree[treeIndex] = merger.merge(tree[leftIndex], tree[rightIndex]); } public E query(int queryL, int queryR) { if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length) { throw new IllegalArgumentException("not exist"); } return queryHelp(0, 0, data.length - 1, queryL, queryR); } private E queryHelp(int treeIndex, int l, int r, int queryL, int queryR) { if (queryL == l && queryR == r) { return tree[treeIndex]; } int mid = l + (r - l) / 2; int leftIndex = leftChild(treeIndex); int rightIndex = rightChild(treeIndex); if (queryR <= mid) {// 结果在左子树 return queryHelp(leftIndex, l, mid, queryL, queryR); } else if (queryL > mid) { return queryHelp(rightIndex, mid + 1, r, queryL, queryR); } // 结果分布在两边 E leftResult = queryHelp(leftIndex, l, mid, queryL, mid); E rightResult = queryHelp(rightIndex, mid + 1, r, mid + 1, queryR); return merger.merge(leftResult, rightResult); } public void set(int index, E val) { if (index < 0 || index >= data.length) { new IllegalArgumentException("error"); } set(0, 0, data.length-1, index, val); } private void set(int treeIndex, int l, int r, int index, E val) { if (r == l) { tree[treeIndex] = val; return; } int mid = l + (r - l) / 2; int leftIndex = leftChild(treeIndex); int rightIndex = rightChild(treeIndex); if(index <= mid) { set(leftIndex,l,mid,index,val); }else set(rightIndex,mid+1,r,index,val); //因为改变了叶子节点的内容,所以一定要更新其父节点的内容,这是一个联动的效果 tree[treeIndex] = merger.merge(tree[leftIndex], tree[rightIndex]); } private int leftChild(int index) { return 2 * index + 1; } private int rightChild(int index) { return 2 * index + 2; } @Override public String toString() { StringBuilder sb = new StringBuilder(); sb.append("["); for (int i = 0; i < tree.length; i++) { if (tree[i] != null) sb.append(tree[i] + " "); else { sb.append("null "); } } sb.append("]"); return sb.toString(); } }
下面是测试代码

public class Main { public static void main(String[] args) { Integer[] arr = { -2, 0, 3, -5, 2, -1, 1, 3 }; SegmentTree<Integer> seg = new SegmentTree<Integer>(arr,(a,b)->a+b);//这里使用的是lamda表达式 seg.set(1, 1); seg.set(0, 1); seg.set(3, 4); System.out.println(seg.query(0, 4));//求出了数组下标为0 - 4 的和 } }
10.dfs
11.bfs
12.必备的技巧
12.1 状态压缩
定义:简单来说就是某种状态需要由多个变量/元素确定,但是我们用一种方法将状态 压缩成一个或者更少的变量/元素就可以表示这个状态
如:二维数组用一个变量来表示。
数组大小为row*col
则:v = x * row + col //用一个v来存储这种状态 i = v / col //转换回去 j = v % col
12.2 取模的技巧(用于处理非常大的数据)
(a * b) % c = ((a % c) * (b % c) ) % c
(a + b) % c = ((a % c) + (b % c) ) % c
12.3 钟表类型的计算
比如一个数字只在0-12,当12 再加 1 就变成 0
那么 num = num % 12 ;
利用这个将减法变成加法 还是上面的例子,一个数减1 就等于这个数加 12
比如:0 - 1 = 12
转换成 0 + 12 = 12
也就是 (num-1) % 12 = (num+12)%12
这里只是举了一个特例 取余的那个数为 12 。具体遇到特殊情况,特殊对待
12.4 字符转数字互转换
将字符减去 '0' 的到的就是数字
Character.forDigit(int digit, int radix);//将数字转换成字符
12.5“四 / 八联通”
四联通:
设置一个二维数组为dirs[4][2] = [ [-1,0] , [0,1] , [1,0], [-1,0] ] //分别代表上,右,下,左
for (int d = 0; d < 4; d++) { nextx = x + dirs[d][0]; nexty = y + dirs[d][1]; }
八连通:
for (int i = -1; i < 2; i++) {//-1 0 1 for (int j = -1; j < 2; j++) { // -1 0 1 if(i==0 && j==0) //排除自身,剩下的就是8个方向 continue; //..... } }
通常用于dfs的搜索
12.6斐波那契数列
前面提到了可以利用矩阵来快速计算斐波那契数列的第n项
在这里直接给出公式,感兴趣原理的,可以自己去查寻相关资料。
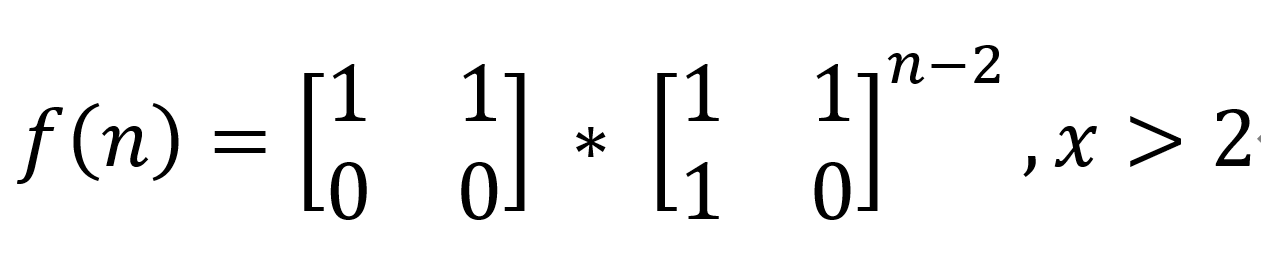

static int[][] m= { {1,1}, {1,0} }; static int N = m.length; /** * 通常快速求斐波那契数列需要结合BigInteger来使用,或者需要取余。这里没有考虑。 */ public static void main(String[] args) { for(int i=1;i<40;i++) {//从第3项开始的前n项和 int[][] res = quickExp(m,i); int[][] init = {{1,1},{0,0}}; init = multiple(init, res); System.out.println(init[0][0]); } } private static int[][] quickExp(int[][] m, int n) { int[][] res = new int[N][N]; for(int i=0;i<N;i++) { for (int j = 0; j < N; j++) { if(i == j) res[i][j] = 1; else res[i][j] = 0; } } while(n>0) { if((n & 1) == 1) res = multiple(res, m); m = multiple(m, m); n = n>>1; } return res; } private static int[][] multiple(int[][] m1, int[][] m2) { int[][] res = new int[m1.length][m2[0].length]; for(int i=0;i<m1.length;i++) { for(int j=0;j<m2[i].length;j++) { for(int k=0;k<m2.length;k++) { res[i][j] += m1[i][k]* m2[k][j]; } } } return res; }
更多更全的代码及内容:https://github.com/zhanyha/lanqiao




 浙公网安备 33010602011771号
浙公网安备 33010602011771号