求数组所有区间最大值减去最小值之差的和(贝壳笔试题)

这个题直接暴力求解的话时间复杂度肯定是不行的，所以，我们要计算每个数值的贡献，对每一个数求他当最小值当了多少次，当最大值当了多少次，最后当最大值的次数乘以这个数值减去当最小值的次数乘以数值就得到这个数的贡献，依次把这n个数的贡献加起来就是整个极差之和。

在计算一个数当了多少最值的时候，我们要理解问题，因为区间是连续的，所以，以最小值为例，如果一个数是当前这段区间的最小值，那么他一定是当前这段区间最小的(这不废话)，所以，我们就找到他往左做多能找到多少个连续的数都比他大，记录这个位置，同理找他右边有多少个大于它的，这样就得到一个区间，这个区间是以这个数位最小值，如下图示可以比较直观的理解。

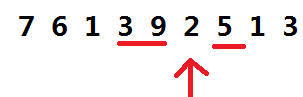
加入找以2为最小值的区间，那么他最多可以往左找到3，往右最多可以找到5，那么2作为最小值构成的区间数目为(2+1) * (1+1)，如下：

[3, 9, 2], [9, 2], [2], [3, 9, 2, 5], [9, 2, 5], [2, 5]

同理如果2作为最大值也一样求，最大值区间只有[2]这个区间

这个题目还有一个小技巧就是在预处理每个元素作为最值时，最左到什么位置和最右到什么位置，可以利用已知信息，就是前一个求出的位置来跳着加速，使得时间复杂度不是O(n^2)

代码：

#include <bits/stdc++.h>

using namespace std;

const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
int a[maxn];
int L[maxn], R[maxn];
void print(int L[], int n)
{
    for (int i = 1; i <= n; i++)
        printf("%d ", L[i]);
    puts("");
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    a[0] = -1, a[n + 1] = -1;
    int sum_min = 0;
    //求以当前元素作为最小值时，最左可以扩展到的元素位置.
    for (int i = 1; i <= n; i++)
    {
        if (a[i] >= a[i - 1])
            L[i] = i;
        else
        {
            int tmp = i - 1;
            while (a[i] < a[tmp])
            {
                if (tmp == L[tmp])
                    tmp--;
                else
                    tmp = L[tmp];
            }
            L[i] = tmp + 1;
        }
    }
    //print(L, n);
    //求以当前元素作为最小值时，最右可以扩展到的元素位置.
    for (int i = n; i >= 1; i--)
    {
        if (a[i] >= a[i + 1])
            R[i] = i;
        else
        {
            int tmp = i + 1;
            while (a[i] < a[tmp])
            {
                if (tmp == R[tmp])
                    tmp++;
                else
                    tmp = R[tmp];
            }
            R[i] = tmp - 1;
        }
    }
    //print(R, n);
    //求作为最小值时每个元素的贡献，最后需要减去
    for (int i = 1; i <= n; i++)
    {
        int tmp = (i - L[i] + 1) * (R[i] - i + 1);
        sum_min += tmp * a[i];
    }
    a[0] = inf, a[n + 1] = inf;
    int sum_max = 0;
    //求以当前元素作为最大值时，最左可以扩展到的元素位置.
    for (int i = 1; i <= n; i++)
    {
        if (a[i] <= a[i - 1])
            L[i] = i;
        else
        {
            int tmp = i - 1;
            while (a[i] > a[tmp])
            {
                if (tmp == L[tmp])
                    tmp--;
                else
                    tmp = L[tmp];
            }
            L[i] = tmp + 1;
        }
    }
    //print(L, n);
    //求以当前元素作为最大值时，最右可以扩展到的元素位置.
    for (int i = n; i >= 1; i--)
    {
        if (a[i] <= a[i + 1])
            R[i] = i;
        else
        {
            int tmp = i + 1;
            while (a[i] > a[tmp])
            {
                if (tmp == R[tmp])
                    tmp++;
                else
                    tmp = R[tmp];
            }
            R[i] = tmp - 1;
        }
    }
    //print(R, n);
    //元素作为最大值时的贡献
    for (int i = 1; i <= n; i++)
    {
        int tmp = (i - L[i] + 1) * (R[i] - i + 1);
        sum_max += tmp * a[i];
    }
    printf("%d\n", sum_max - sum_min);
    return 0;
}