矩阵快速幂(入门) 学习笔记hdu1005, hdu1575， hdu1757

矩阵快速幂是基于普通的快速幂的一种扩展，如果不知道的快速幂的请参见http://www.cnblogs.com/Howe-Young/p/4097277.html。二进制这个东西太神奇了，好多优秀的算法都跟他有关系，这里所说的矩阵快速幂就是把原来普通快速幂的数换成了矩阵而已，只不过重载了一下运算符*就可以了，也就是矩阵的乘法，  当然也可以写成函数，标题中的这三个题都是关于矩阵快速幂的基础题。拿来练习练习熟悉矩阵快速幂，然后再做比较难点的，其实矩阵快速幂比较难的是构造矩阵。下面还是那题目直接说话：

hdu1575：

题目大意：求一个矩阵k此方之后主对角线上的元素之和对9973取模

这个题是矩阵快速幂的裸题，直接用就行了。下面是代码

#include<iostream>
#include <string.h>
#include <stdio.h>
#include <algorithm>

using namespace std;
const int N = 11;
const int mod = 9973;
struct Matrix{
    int a[N][N];
};
int n;
Matrix operator * (Matrix t1, Matrix t2)//重载运算符 *  
{
    Matrix c;
    memset(c.a, 0, sizeof(c.a));
    //矩阵乘法 
    for (int k = 0; k < n; k++)
    {
        for (int i = 0; i < n; i++)
        {
            if (t1.a[i][k] <= 0)
                continue;
            for (int j = 0; j < n; j++)
            {
                if (t2.a[k][j] <= 0)
                    continue;
                c.a[i][j] = (c.a[i][j] + t1.a[i][k] * t2.a[k][j]) % mod;
            }
        }
    }
    return c;
}
//重载^运算符 
Matrix operator ^ (Matrix t, int k)
{
    Matrix c;
    memset(c.a, 0, sizeof(c.a));
    //初始化矩阵c为单位阵 
    for (int i = 0; i < n; i++)
    {
        c.a[i][i] = 1;
    }
    //这里用到快速幂 
    for (; k; k >>= 1)
    {
        if (k & 1)
            c = c * t;
        t = t * t;
    }
    return c;
}
int main()
{
    int T, k;
    cin >> T;
    while (T--)
    {
        cin >> n >> k;
        Matrix t1, t2;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
                cin >> t1.a[i][j];
        }
        t2 = t1 ^ k;
        int res = 0;
        for (int i = 0; i < n; i++)
            res = (res + t2.a[i][i]) % mod;
        cout << res << endl;
    }

    return 0;
}

hdu1005：

题目大意：

f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.

给你A， B和n让你求f(n)是多少

这个题就需要稍微构造一下矩阵了

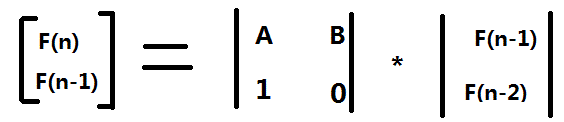
这样的话要求F(n)的话，只需要对求出来F(n-1)就行了，对应的F(n-1)要求出F(n-2)，所以题目给了F(1)和F(2)，所以乘以他前面的系数矩阵就为【F(3), F(2)】^T,再接着成系数矩阵就为【F(4)，F(3)】^T所以要求F(n)只需要对系数矩阵进行n-2次幂就行了，然后最后要求的结果就是矩阵的第一行第一列的结果，代码如下

#include<iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;
const int N = 2;
const int mod = 7;
struct Matrix
{
    int mat[N][N];
};
//矩阵乘法(函数的形式) 
Matrix Multi(Matrix a, Matrix b)
{
    Matrix c;
    memset(c.mat, 0, sizeof(c.mat));
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            for (int k = 0; k < N; k++)
                c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) % mod;
        }
    }
    return c;
}
//矩阵快速幂 （函数形式） 
Matrix quickMatrixPower(Matrix a, int k)
{
    Matrix t;
    memset(t.mat, 0, sizeof(t.mat));
    for (int i = 0; i < N; i++)
        t.mat[i][i] = 1;
    //快速幂 
    while (k)
    {
        if (k & 1)
            t = Multi(t, a);
        a = Multi(a, a);
        k >>= 1;
    }
    return t;
}

int main()
{
    long long a, b, n;
    while (cin >> a >> b >> n && (a + b + n))
    {
        Matrix t;
        //初始化系数矩阵 
        t.mat[0][0] = a; 
        t.mat[0][1] = b;
        t.mat[1][0] = 1;
        t.mat[1][1] = 0;
        if (n >= 3)
        {
            t =  quickMatrixPower(t, n - 2);
            printf("%d\n", (t.mat[0][0] + t.mat[0][1]) % mod);
        }
        else
        {
            printf("%lld\n", n);
        }
    }


    return 0;
}

hdu1757

题目大意：

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

这个关键还是在于构造矩阵，因为给递推式了，所以矩阵还是比价好构造的，下图是构造的矩阵

推到过程类似于1005，不再赘述，代码如下：

#include<iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
const int ori[1][10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0}; 
struct Matrix
{
    int str[10][10];
};
int m;
//矩阵乘法 
Matrix operator * (Matrix a, Matrix b)
{
    Matrix c;
    memset(c.str, 0, sizeof(c.str));
    for (int i = 0; i < 10; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            for (int k = 0; k < 10; k++)
                c.str[i][j] = (c.str[i][j] + a.str[i][k] * b.str[k][j]) % m;
       }
    }
    return c;
}
//矩阵快速幂 
Matrix power (Matrix a, int k)
{
    Matrix c;
    memset(c.str, 0, sizeof(c.str));
    for (int i = 0; i < 10; i++)
        c.str[i][i] = 1;
    while (k)
    {
        if (k & 1)
            c = c * a;
        a = a * a;
        k >>= 1;
    }
    return c;
}
//最后一步的矩阵乘法 
int Multi(Matrix a)
{
    Matrix c;
    memset(c.str, 0, sizeof(c.str));
    for (int i = 0; i < 1; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            for (int k = 0; k < 10; k++)
            {
                c.str[i][j] = (c.str[i][j] + ori[i][k] * a.str[k][j]) % m;
            }
        }
    }
    return c.str[0][0] % m;
}
int main()
{
    int k;
    while (cin >> k >> m)
    {
        Matrix t;
        memset(t.str, 0, sizeof(t.str));
        for (int i = 0; i < 10; i++)
        {
            cin >> t.str[i][0];
            for (int j = 0; j < 10; j++)
                if (i + 1 == j)
                    t.str[i][j] = 1;
        }
        if (k >= 10)
        {
            t = power(t, k - 9);
            printf("%d\n", Multi(t));
        }
        else
        {
            printf("%d\n", k);
        }
    }

    return 0;
}