01背包-dp

一 问题分析

二 代码实现

package Dp_0_1_bag;
import java.io.BufferedWriter;
import java.io.FileWriter;
import java.io.IOException;

public class bin
{

    public static void main(String[] args) throws IOException
    {
        int c=10;
        int []w= {0,2,2,6,5,4};
        int []v= {0,6,3,5,4,6};
        dp_0_1_Bag myDp_0_1_Bag=new dp_0_1_Bag(w, v, c);
    }

}
class dp_0_1_Bag
{
    int m[][];   //动态规划   最优解值记录
    int w[];     //重量
    int c;       //背包容量
    int v[]; 	 //价值
    int x[];     //最优解
    public dp_0_1_Bag(int w[],int v[],int c) throws IOException
    {
        this.m=new int [w.length][c+1];
        this.x=new int [w.length];
        this.v=v;
        this.w=w;
        this.c=c;
        Dp_0_1_Bag();
        traceback();
        display();
    }
    public void Dp_0_1_Bag()
    {
        for(int i=0; i<w.length; i++)
        {
            m[i][0]=0;     //背包容量为0
        }
        for(int j=0; j<=c; j++)
        {
            m[0][j]=0;     //没有物品可以装
        }
        for(int i=1; i<w.length; i++)
        {
            for(int j=1; j<w[i]; j++)   //装不进去
            {
                m[i][j]=m[i-1][j];
            }
            for(int j=w[i]; j<=c; j++)   //可以装进去
            {
                m[i][j]=Math.max(m[i-1][j], (m[i-1][j-w[i]]+v[i]));
            }
        }
    }
    public void traceback()
    {
        for(int i=w.length-1; i>=1; i--)
        {
            if(m[i][c]==m[i-1][c])
            {
                x[i]=0;
            }
            else 
            {
                x[i]=1;
                c-=w[i];
            }
        }
    }
    public void display() throws IOException
    {
        BufferedWriter fout=new BufferedWriter(new FileWriter("out.txt"));
        fout.write("m[i][j]");
    	fout.newLine();
    	for(int i=0; i<w.length; i++)
    	{
    		for(int j=0; j<=c; j++)
        	{
    			fout.write(""+m[i][j]+"\t");
        	}
    		fout.newLine();
    	}
    	fout.flush();
    	fout.write("x[i]");
    	fout.newLine();
    	for(int i=1; i<x.length; i++)
    	{
    		fout.write(""+x[i]);
    		fout.newLine();
    	}
    	fout.flush();
    }
}

三 运行结果

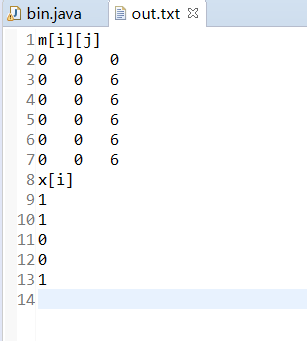
四 收获

1. 将背包重量离散化

2. 自我认为dp算法也是一种高明的枚举迭代策略

3. dp算法的关键在于分析子结构，得出递归方程

4. 五 不足

   这个算法如果在背包容量很大的情况下，算法复杂度将会倍增