并查集入门

并查集介绍

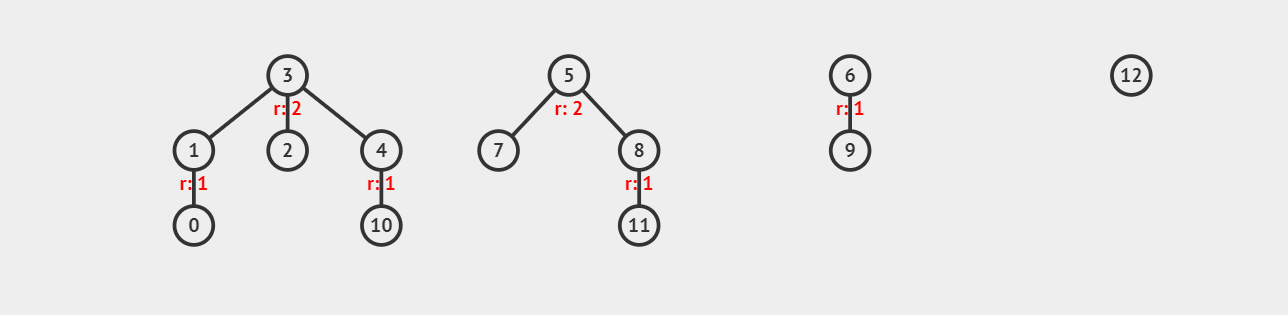
并查集是一种树形的数据结构，我们可以使用它来进行集合上的合并与查询等问题。具体来说，它支持两种操作：

合并：将两个集合合并成一个集合。
查询：确定某个元素处于哪个集合。

如图，\(\{3, 1, 2, 4, 0, 10\}\) 表示一个集合，\(\{5, 7, 8, 11\}\) 表示另一组集合。

可以看出并查集是多叉树结构，我们用根节点来表示这个根节点所在的集合(即根节点作为集合的"代表元素")。

基础并查集

初始化

在我们初始创建数据的时候，由于没有任何操作，所以每个元素都是一个独立的集合，显然，每个元素都是本身集合的根节点。

for (int i = 0; i < n; i ++ ) p[i] = i; // p(i) 表示i的父节点

查询

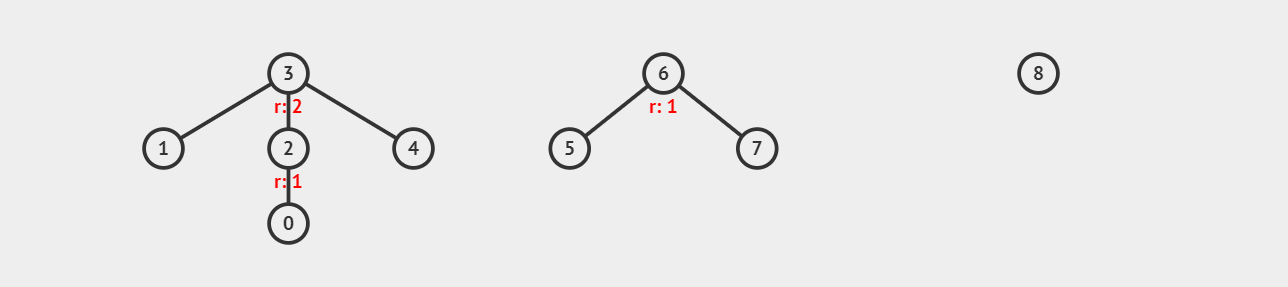
假设我们现在要查询元素 \(0\) 的父节点，该怎么做呢？

很简单，由于根节点的父节点就是本身（不知道的可以回顾一下初始化过程）。所以我们直接检查 \(0\) 的父节点是否为 \(0\) 即可。

如果 \(0\) 父节点为 \(0\) ，说明 \(0\) 是所属集合的根节点，返回 \(0\) 即可。（因为我们用根节点代表集合）
如果 \(0\) 父节点不为 \(0\) ，那么我们只需要递归检查它的父节点是否为 \(0\) 即可。

我们发现 \(0\) 的父节点是 \(2\) ，那么我们继续检查 \(2\) 是否为根节点(\(p[2] == 2\)) ，不是，则继续检查 \(3\) ，此时 \(3\) 为根节点，于是返回 \(3\) 。

查询的复杂度为被查询元素在树上的深度。

int find (int x) // find函数用来返回x所属集合的代表元素(根节点)
{
    return p[x] == x ? x : find(p[x]);
}

合并

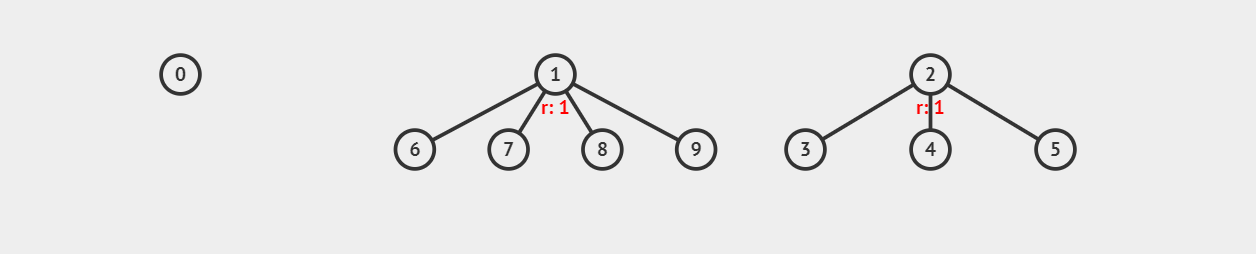
如图，如何合并 \(6\) 所属集合和 \(3\) 所属集合？由于我们知道根节点代表整个集合，合并 \(6\) 和 \(3\) 即意味着它们合并后根节点相同，我们可以任意取一个子集的根节点作为合并后的根节点，比如取 \(3\) 后：

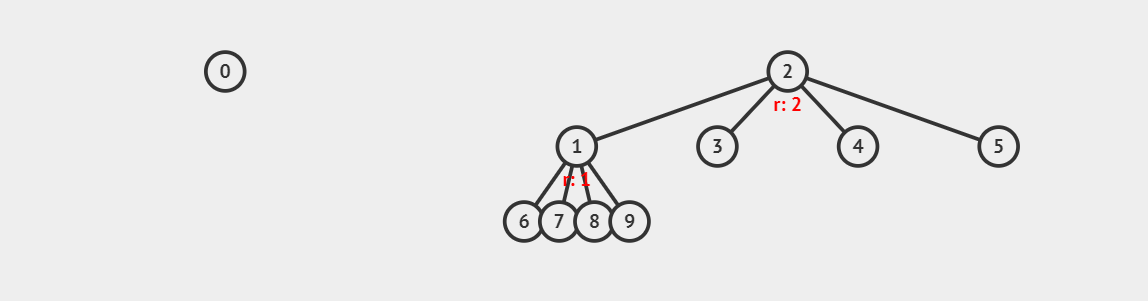
我们选择了把 \(2\) 作为合并后集合的根节点（代表元素）。

void merge (int x, int y)
{
    x = find(x), y = find(y); // x 和 y 为根节点
    p[x] = y; // 直接把其中一个集合合并到另外一个集合
}

并查集优化

路径压缩

我们发现，由于每次查询某个元素需要查询 \(r\) 次(\(r\) 为当前元素在树上的深度)，当树的深度很大，且我们要查询的元素在很深的地方，那么查询所需要耗费的时间就很大，有没有办法优化呢？

答案是肯定的，我们发现，整个集合只有代表元素是'有用'的，其他元素仅能代表它在这个集合中，与它所处的位置没有关系。 于是，我们在每次查询后，就把当前元素的父节点设置为集合的根节点，根节点就是 \(find\) 的返回值，所以：

int find (int x) // find 函数返回x所属集合代表元素
{
    return p[x] == x ? x : p[x] = find(p[x]); // 把x的父节点设置为根节点
}

按秩合并（启发式合并）

上述提到，树的深度会影响查询的速度，那么我们可以在合并的时候，把集合元素较少的合并到集合元素较大的即可。还可以按照集合树的深度与集合的元素数量评估来得到更好的合并方法。

void merge (int x, int y) // 按秩合并需要用到集合内的数量
{
    x = find(x), y = find(y);
    if (siz[x] > siz[y]) swap(x, y);
    siz[y] += siz[x];
    p[x] = y;
}

按秩合并在竞赛中不常用，一般来说路径压缩就已经够用了。

模板

const int N = 200010;

int p[N]; // p(i)表示i的父节点

void init (int n)
{
    for (int i = 0; i < n; i ++ ) p[i] = i;
}

int find (int x)
{
    return p[x] == x ? x : p[x] = find(p[x]);
}

void merge (int x, int y)
{
    x = find(x), y = find(y);
    p[x] = y;
}

习题

模板并查集

朋友此题也可以使用维护集合数量的并查集

村村通

超市贪心+并查集

维护集合数量的并查集

有时候，我们只维护元素所属的集合是不够的，我们还需要知道集合内的数量。

只维护一个集合数量，和基础并查集无任何区别，只需要加上一个 \(siz\) 数组维护每个集合内的数量即可。

需要变的就是在合并集合时的操作，以及初始化集合数量：

void init (int n)
{
    // 一开始每个元素都是独立的集合，集合内元素数量为1
    for (int i = 1; i <= n; i ++ ) p[i] = i, siz[i] = 1; 
}

void merge (int x, int y) // 按秩合并需要用到集合内的数量
{
    x = find(x), y = find(y);
    siz[y] += siz[x];
    p[x] = y;
}

带权并查集

当然，维护了数量在某些情况也是不够用的，我们还需要知道集合内各个元素的关系。我们可以使用带权并查集，使用边权来维护当前元素与父节点的某种关系。

即，带权并查集可以维护元素之间的制约关系。

我们以一道经典例题食物链为例。

例题食物链

题意

动物王国中有三类动物 \(A,B,C\)，这三类动物的食物链构成了有趣的环形。

\(A\) 吃 \(B\)，\(B\) 吃 \(C\)，\(C\) 吃 \(A\)。

现有 \(N\) 个动物，以 \(1∼N\) 编号。

每个动物都是 \(A,B,C\) 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 \(N\) 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 \(X\) 和 \(Y\) 是同类。

第二种说法是 2 X Y，表示 \(X\) 吃 \(Y\)。

此人对 \(N\) 个动物，用上述两种说法，一句接一句地说出 \(K\) 句话，这 \(K\) 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 \(X\) 或 \(Y\) 比 \(N\) 大，就是假话；
当前的话表示 \(X\) 吃 \(X\)，就是假话。

你的任务是根据给定的 \(N\) 和 \(K\) 句话，输出假话的总数。

分析

给出两个动物，它们有吃、被吃以及同类三种制约关系，而带权并查集可以很好地维护元素间的制约关系。

设 \(d[x]\) 表示元素 \(x\) 与其父节点的边的边权。

规定：

\(d[x] \% 3 = 0\) 表示 \(x\) 与父节点 \(p[x]\) 是同类。
\(d[x] \% 3= 1\) 表示 \(x\) 可以吃父节点 \(p[x]\)。
\(d[x] \% 3 = 2\) 表示 \(x\) 可以被父节点 \(p[x]\) 吃。

那么我们判定假话，只需要不满足 \(d[x]\) 即可。

简单来说：

判断 \(x\) 与 \(y\) 为同类，但已经制约了 \(x\) 和 \(y\) 为异类（吃或被吃）。
判断 \(x\) 吃 \(y\) ，但已经制约了 \(x\) 和 \(y\) 是同类或者 \(x\) 被 \(y\) 吃。
判断 \(x\) 被 \(y\) 吃，但已经制约了 \(x\) 和 \(y\) 是同类或者 \(x\) 被 \(y\) 吃。（题目不会给定）

首先我们肯定要是有路径压缩来优化查询的，在路径压缩后， \(x\) 对应的父节点变为集合根节点，因此 \(d[x]\) 也需要做变换。

int find (int x)
{
    if (x != p[x])
    {
        int u = find(p[x]);
        /*
         * 注意此时x还没有路径优化，父节点仍然保持原来的父节点
         * 此时 x 以上的节点经过路径优化，d[p[x]] 也修改为正确值(x父节点与根节点的关系)
         * 那么我们只需要根据x与父节点的关系、x父节点与根节点的关系即可传递得到x与根节点的关系，再路径优化即可。
        */
        d[x] += d[p[x]];
        p[x] = u;
    }
    return p[x];
}

那么现在的问题就是，如何知道一个集合里两个元素的制约关系？

由于我们求得 \(d[x]\) 都是 \(x\) 与根节点的关系，那么 \((d[x] - d[y]) \% 3\) 即为 \(x\) 与 \(y\) 的制约关系。

如何合并两个关系呢？

假设判定 \(x\) 和 \(y\) 的关系的边权表示为 \(op\) ，由于在 \(find\) 中我们可以求得 \(x\) 、 \(y\) 分别与其根节点的关系，且现在 \(x\) 与 \(y\) 的制约关系也知道了，那么根据传递性我们也可以求出两个集合根节点之间的制约关系，合并两个集合时维护好两个根节点的制约关系即可。

假设 \(x\) 的根节点为 \(px\) ，\(y\) 的根节点为 \(py\) 。现在要把 \(px\) 合并到 \(py\) 。

判定 \(x\) 与 \(y\) 同类

在合并后的集合里，\(x\) 与 \(y\) 的关系应该为 \((d[x] - d[y]) \% 3 = 0\) 。由于此时的 \(d[x]\) 是合并后的，所以合并前应该为 \(d[x] + d[px]\) 。即 \(d[x] + d[px] - d[y] = 0\) ，那么 \(d[px] = d[y] - d[x]\) 。
判定 \(x\) 与 \(y\) 不同类

由于题目给定此时判定为 \(x\) 吃 \(y\) ，所以我们只需要考虑这一种。

在合并后的集合里，\(x\) 与 \(y\) 的关系用应该是：\(d[x] - d[y] = 1\) ，即 \(x\) 可以吃根节点（路径压缩后的父节点），且根节点与 \(y\) 同类，依次推类。

同样此时的 \(d[x]\) 是合并后的，合并前应该是 \(d[x] + d[px]\) ，所以 \(d[x] + d[px] - d[y] = 1\) ，即 \(d[px] = 1 + d[y] - d[x]\) 。

Code

#include <iostream>
using namespace std;

const int N = 50010;

int n, m;
int p[N], d[N];

int find (int x) {
    if (p[x] != x) {
        int t = find(p[x]);
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main () {
    scanf("%d%d", &n, &m);
    
    for (int i = 1; i <= n; i++) p[i] = i;
    
    int res = 0;
    while (m--) {
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);
        
        if (x > n || y > n) res++; // 谎言1：动物编号超出限制
        else {
            int px = find(x), py = find(y);
            if (t == 1) {
                if (px == py && (d[x] - d[y]) % 3) res++; // 谎言2：判定同类，但已经制约x和y是异类
                else if (px != py) { // 否则认为是真话，加上此制约关系
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            }
            else {
                if (px == py && (d[x] - d[y] - 1) % 3) res++; // 谎言3：判定x吃y，但已经制约x和y是同类或者x被y吃
                else if(px != py) { // 否则认为是真话，加上此制约关系
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }
    
    cout << res << endl;
    return 0;
}

习题

关押罪犯也可以使用二分图解决

奇偶游戏同样也可以使用二分图

拓展域并查集

拓展域并查集和带权并查集功能相同，都是对各个元素的不同关系进行制约。由于拓展域需要对同一个元素开多个域，因此空间复杂度较高，除此之外可以完全代替带权并查集。

同样，我们使用食物链这个例子来实现拓展域。

对于元素 \(x\) ，其他元素 \(y\) 和它一共有三种关系：

与 \(x\) 是同类。
被 \(x\) 吃，即 \(x\) 捕食 \(y\) 。
吃 \(x\) ，即 \(x\) 天敌为 \(y\) 。

对于元素 \(x\) ，我们开三个域来表示这三种关系。由于一共有 \(n\) 个动物，我们有一个很好的开域的方式：我们令 \(p[x]\) 表示 \(x\) 的天敌域， \(p[x + n]\) 表示 \(x\) 的同类域， \(p[x + 2 * n]\) 表示 \(x\) 的捕食域 ，那么谎话只有以下两种：

判定 \(x\) 与 \(y\) 是同类，但是 \(x\) 的捕食域或者天敌域存在 \(y\) 。
判定 \(x\) 吃 \(y\) ，但是 \(x\) 的同类域或者天敌域存在 \(y\) 。

在合并的过程，比如合并 \(x\) 和 \(y\) 是同类，那么 \(x\) 的天敌也同样是 \(y\) 的天敌，即也需要合并 \(x\) 与 \(y\) 的天敌域。捕食域同理。

通过上述分析，我们可以很简洁地写出如下代码：

#include <iostream>
#include <numeric>
#include <functional>
using namespace std;

const int N = 200010;
int p[N]; // 拆点，每个点有三个域，天敌域，同类域，捕食域

// 每个集合里的元素都是一类

int main ()
{
    function<int(int)> f = [&](int x) { return x == p[x] ? x : p[x] = f(p[x]); } ;
    function<void(int, int)> mg = [&](int x, int y) { p[f(x)] = f(y); };
    
    int n, k, d, x, y, ret = 0; cin >> n >> k;
    iota(p + 1, p + 3 * n + 1, 1);
    while(k -- && cin >> d >> x >> y)
    {
        if (x > n || y > n) { ret ++ ; continue; } // 假话2
        if (d == 2 && x == y) { ret ++ ; continue; } // 假话3
        // 假话1，产生冲突
        if (d == 1)
        {
            // 如果判定x和y是同类，但是x的天敌域或者捕食域有y，一定是假话
            if (f(x) == f(y + n) || f(x + 2 * n) == f(y + n)) { ret ++ ; continue; }
            // 否则这是一句真话，记录一下
            mg(x + n, y + n);
            mg(x, y); // x的天敌和y的天敌是同一类
            mg(x + 2 * n, y + 2 * n); // x的捕食域和y的捕食域也是一类
        }
        else
        {
            // 如果判定x捕食y，但是x同类域或天敌域有y，假话
            if (f(x + n) == f(y + n) || f(x) == f(y + n)) { ret ++ ; continue; }
            mg(x + 2 * n, y + n);
            mg(x + n, y); // y的天敌域加上x的同类域
            mg(x, y + 2 * n); // x的天敌域加上y的捕食域
            
        }
    }
    cout << ret << endl;
    return 0;
}

posted @ 2022-02-17 22:16 Horb7 阅读(287) 评论(0) 编辑收藏举报

刷新页面返回顶部

Horb7