线段树入门

线段树介绍

线段树是一种基于分治思想的二叉树结构，用于在区间上进行高效的信息统计。

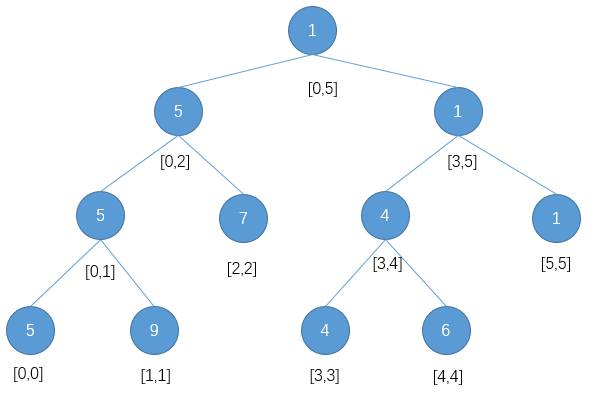
如图是一般的线段树结构，我们可以发现：

1. 线段树的每个节点都代表一个区间，且按照深度递增，代表的区间逐渐缩小。
2. 线段树是单独的一棵树，具有唯一的根节点，它代表需要统计信息的整个区间。
3. 线段树的每个叶子节点都代表一个长度为 $1$ 的区间 $[x, x]$ 。
4. 对于每个非叶子结点 $[l, r]$ ，它的左节点为 $[l, mid]$ ，右节点为 $[mid+1, r]$ ，其中 $mid = (l + r) / 2$ 。

如果去除最后一层，那么线段树是一棵完全二叉树，因此我们可以采用与二叉堆类似的存储形式：

1. 根节点编号为 $1$ 。
2. 对于非叶子节点 $p$ ，左节点为 $p \times 2$ ，右节点为 $p \times 2 + 1$ 。

需要注意的是，最后一层是不满的，我们需要空出数组的位置来表示空节点。

除去最后一层，由于最后第二层最多有 $n$ 个节点，因此满二叉树需要 $n + \dfrac n 2 + \dfrac n 4 + \ldots + 1 = 2 \times n - 1$ 个节点。

最后一层需要开 $n \times 2$ 个节点，因此我们需要至少 $n \times 4$ 的空间存储，才能保证数组不会越界。

---

线段树的建树

线段树的基本用途是维护序列的某些属性，最基本的线段树具有查询和修改两个功能。给定长度为 $[1, n]$ 的序列，我们可以按 $[1, n]$ 的区间建一棵线段树。线段树基于分治思想，需要从上往下构建。递归完成后也可以方便地从下往上传递信息。

下面以维护区间最大值为例。

struct seg_tree
{
    #define lc(p) (p<<1)
    #define rc(p) (p<<1|1)
    int l, r; // 节点的信息，维护 [l, r] 区间内的信息
    int maxv; // 需要在区间上维护的信息
};

const int N = 100010; // 假设序列最长长度为 N
seg_tree t[N << 2];
int a[N]; // 原序列

void build (int p, int l, int r) // 当前构建的节点及其需要维护的区间
{
    t[p].l = l, t[p].r = r;
    if (l == r) { t[p].maxv = a[l]; return; } // 到达叶子节点，不需要再往下创建节点
    int mid = l + r >> 1; // 否则创建左节点 [l, mid] 和右节点 [mid+1, r]
    build(lc(p), l, mid), build(rc(p), mid+1, r);
    // 构建完后需要维护这个区间的信息，由于已经创建好左节点(左边一半区间)和右节点(右边一半区间)，根据这两个节点来维护
    t[p].maxv = max(t[lc(p)].maxv, t[rc(p)].maxv);
}

build(1, 1, n); // 从根节点1开始，它维护的是整个区间[1, n]

在线段树的单点修改过程中，每一层只会被调用一次，而线段树的高度为 $log n$ ，因此复杂度为 $log n$ 。

---

线段树的单点修改

利用线段树递归从下往上传递信息的结构，我们也可以很方便地修改某一个元素。

叶子节点代表单个长度的区间，也就是具体的某一个元素。我们可以递归地找到需要修改的叶子节点，在回溯的过程维护它的父节点(代表的区间包括自己的区间，所以也要修改)。

void modify (int p, int x, int v) // 需要把x位置的元素改为v，目前为p节点
{
    if (t[p].l == t[p].r) { t[p].maxv = v; return; } // 已经找到
    int mid = t[p].l + t[p].r >> 1; // 否则判断去左区间找还是去右区间找
    if (x <= mid) modify(lc(p), x, v); // 左区间为[l, mid]，在这个区间内
    else modify(rc(p), x, v); // 右区间为[mid+1, r]
    t[p].maxv = max(t[lc(p)].maxv, t[rc(p)].maxv); // 注意修改完子区间后，当前区间需要维护
}

modify(1, x, v); // 从根节点开始找

---

线段树区间查询

以维护区间最大值的线段树为例，我们查找区间 $[l ,r]$ 的最大值，需要从根节点开始，递归完成：

1. 如果 $[l, r]$ 区间完全覆盖了当前节点的范围，直接返回当前节点维护的信息。
2. 如果左节点和 $[l, r]$ 有交叉，那么递归查询左节点。
3. 如果右节点和 $[l, r]$ 有交叉，那么递归查询右节点。

int query (int p, int l, int r) // 需要查询[l, r]的最大值，当前节点为p
{
    if (l <= t[p].l && r >= t[p].r) return t[p].maxv; // 完全覆盖，节点区间内所有元素都是查询区间内的元素
    int mid = t[p].l + t[p].r >> 1; // 否则查询左节点和右节点
    int maxv = -2e9; // 设为负无穷
    if (l <= mid) maxv = max(maxv, query(lc(p), l, r)); // [l, r]与左节点有交叉
    if (r > mid) maxv = max(query(rc(p), l, r)); // [l, r]与右节点有交叉
    return maxv;
}

cout << query(1, l, r) << endl; // 从根节点开始查询

关于复杂度：

1. 在任意一个节点，只查询它的左节点/右节点。

   显然复杂度是 $O(log n)$ 的。

2. 在某些节点，查询左右节点。

   在左节点，显然又有两种可能，如果只查询一遍，那么可以保证 $O(log n)$ 的复杂度，如果查询左右两边，那么左边一定是被完全覆盖的，因此可以直接回溯。右节点同理。

   所以查询左右节点，本质只是比查询单边多了一次查询，因此复杂度为 $O(2 log n) = O(log n)$ 。

---

线段树的区间修改

假设现在要把 $[l, r]$ 中所有元素加上 $v$ ，一种显然的做法是对 $[l, r]$ 中所有元素执行一次单点修改，但这样的复杂度为 $O(len \times log n)$ 的，最坏情况下修改所有元素，则需要修改整棵树，复杂度 $O(n)$ 。

可以发现，如果我们对区间 $[l, r]$ 中所有元素进行修改，但后面的查询中没有用到 $[l, r]$ 的子区间 ，那么这个修改是无意义的。也就是说，最好的办法就是在查询时才更新当前的区间 。

类似于区间查找，当我们发现某一个节点维护的区间被需要修改的区间覆盖，那么我们修改完当前节点后，直接回溯，不用对其递归修改，比如修改区间 $[1, 10]$ ，当我们递归到节点 $[1, 5]$ 时，就可以修改并回溯。同时我们要给这个节点打上标记，表示当前节点已经修改，但其子区间未修改。

在之后的查询过程中，如果需要使用其子结点，则使用标记的信息更新两个子结点，同时为子结点打上标记，再清除当前节点的标记。

类似于区间查询，区间修改会将区间划分为 $O(log n)$ 个小区间，将复杂度降为 $O(log n)$ 。

下面以例题 [模板]线段树1 为例。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

// 以维护区间和为例
struct seg_tree
{
    #define lc(x) x<<1
    #define rc(x) x<<1|1
    int l, r;
    ll sum, add; // sum为[l, r]区间元素的和，add为懒标记，记录当前这个区间，每个元素加了多少
};

const int N = 100010;
seg_tree t[N << 2];
int a[N], n, m;

void pushup (int p) // pushup操作：自下而上维护每个节点的sum值
{
    t[p].sum = t[lc(p)].sum + t[rc(p)].sum;
}

void pushdown (int p) // pushdown操作：将懒标记下传，将子节点变为真实值
{
    if (!t[p].add) return ; // 如果当前位置没有懒标记，直接返回
    t[lc(p)].sum += t[p].add * (t[lc(p)].r - t[lc(p)].l + 1); // 左节点
    t[rc(p)].sum += t[p].add * (t[rc(p)].r - t[rc(p)].l + 1); // 右节点
    t[lc(p)].add += t[p].add; // 给左节点加懒标记，注意左节点可能已经加过懒标记
    t[rc(p)].add += t[p].add; // 给右节点加懒标记，注意右节点可能已经加过懒标记
    t[p].add = 0; // 清除p的懒标记
}

void build (int p, int l, int r)
{
    t[p].l = l; t[p].r = r;
    if (l == r) { t[p].sum = a[l]; return; } // 到达叶子节点，此时区间长度为1，sum即为此位置的值
    int mid = l + r >> 1;
    build(lc(p), l, mid); build(rc(p), mid+1, r);
    pushup(p); // 使用pushup自下往上维护信息
}

void modify (int p, int l, int r, int v) // 为[l, r]区间所有数字增加v
{
    if (t[p].l >= l && t[p].r <= r) // 当前节点被[l, r]区间覆盖
    {
        // 修改当前区间，打上标记并回溯
        t[p].sum += (ll)v * (t[p].r - t[p].l + 1);
        t[p].add += v;
        return ;
    }
    pushdown(p); // 此时这个点的子节点需要使用，将懒标记下传
    int mid = t[p].l + t[p].r >> 1;
    if (l <= mid) modify(lc(p), l, r, v); // 左节点[t[p].l, mid]有部分被覆盖
    if (r > mid) modify(rc(p), l, r, v); // 右节点[mid+1, t[p].r]有部分被覆盖
    pushup(p); // 子结点被修改，记得维护当前节点
}

ll query (int p, int l, int r)
{
    if (t[p].l >= l && t[p].r <= r) return t[p].sum;
    pushdown(p); // 子节点需要使用，记得下传懒标记
    int mid = t[p].l + t[p].r >> 1;
    ll ret = 0; // 当前节点被[l, r]覆盖的元素的和
    if (l <= mid) ret += query(lc(p), l, r); // 左节点[t[p].l, mid]有部分被覆盖
    if (r > mid) ret += query(rc(p), l, r); // 右节点[mid+1, t[p].r]有部分被覆盖
    return ret;
}

int main ()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    build(1, 1, n); // 在区间[1, n]上建立线段树
    while(m -- )
    {
        int op, l, r, v;
        cin >> op >> l >> r;
        if (op == 1) cin >> v, modify(1, l, r, v);
        else cout << query(1, l, r) << endl;
    }
    return 0;
}

例题

1. 一个简单的整数问题 可以使用树状数组

2. 一个简单的整数问题2 区间加，区间和

3. 进制 维护所有进制

4. 你能回答这些问题吗 比较难的题目，需要维护较多信息

5. 区间最大公约数 更损相减法