CF 1612D. X-Magic Pair

X-Magic Pair

题意

给定两个数字 \(a, b\) ，每次可以把其中一个数字换成 \(|a - b|\) ，问能否经过若干次操作使得其中一个数字变成 \(k\) ?

分析

假设这两个数字为 \(14, 35\) 。我们会发现：

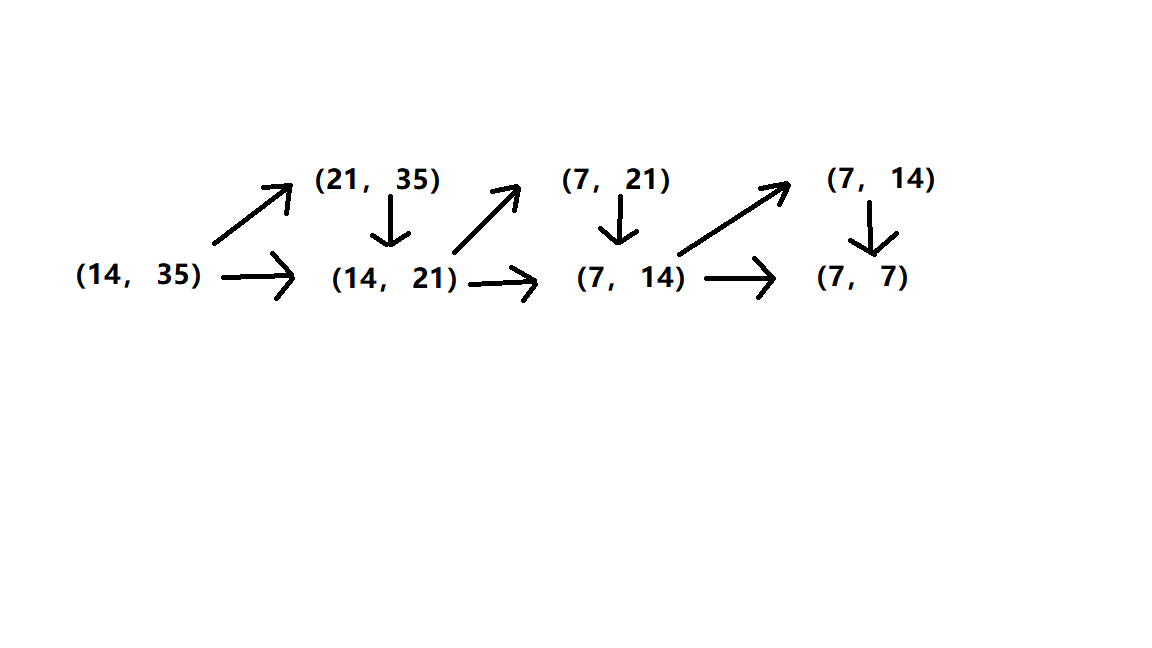
对小的数字进行修改是没有意义的，因为它不会产生新的数字，它只能循环到大数被修改的那一组数字。

那么我们每次只需要对大的数字进行修改就可以了。

void solve ()
{
    int x, y, k; cin >> x >> y >> k;
    if (x > y) swap(x, y);
    while(x) // 不断枚举较小的数字
    {
        if (k == x || k == y) return cout << "YES\n", void();
        y -= x;
        if (x > y) swap(x, y);
    }
    cout << "NO\n";
}

但是这样做，如果 \(a = 1, b = 10^{18}\) 会 \(TLE\) ，考虑函数中， \(y\) 会不断减去 \(x\) 直到小于 \(x\) ，\(k\) 只需要等于其中一个即可。

用取模优化减法，假设 \(y\) 在某次减去 \(x\) 时等于 \(k\) ，那么可以写成 \(y = \alpha x + k\) ，也就是：\(y \equiv k \pmod x\) 。

这个考虑了 \(k\) 为某次 \(y\) 的情况，而如果 \(k\) 为某次 \(x\) ，那么在 \(y\) 取模后， \(x\) 自然变成了 \(y\) ，也能解决。

void solve ()
{
    int x, y, k; cin >> x >> y >> k;
    if (x > y) swap(x, y);
    while(x) // 不断枚举较小的数字
    {
        if (y % x == k % x && k <= y) return cout << "YES\n", void();
        y %= x;
        swap(x, y);
    }
    cout << "NO\n";
}