对顶堆

对顶堆

什么是对顶堆

对顶堆是一种数据结构，它可以动态地维护某一个临界值，如前 $i$ 个数字的中位数、 前 $i$ 个数字中第 $k$ 小的值等。

对顶堆一般适用一个大根堆维护前面某个状态，小根堆维护后面不同的状态（如大于/小于中位数等）。

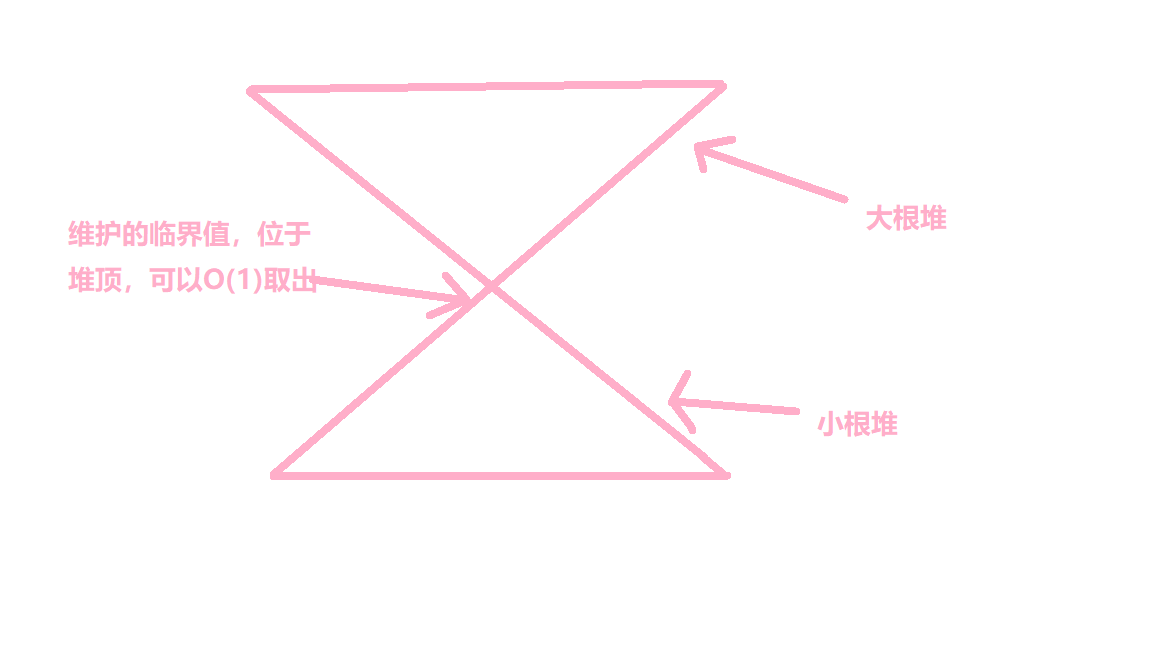
我们只需要调整两个堆的元素数量，即可 $O(1)$ 地取出需要维护的值。

例题

动态中位数

题意

每次插入一个数字，当序列中数字数量为奇数时，输出序列的中位数。

分析

假设当前序列长度为 $n$ 。

开一个大根堆来维护当前序列中前 $[1, n / 2]$ 小的元素，再开一个小根堆来维护当前序列前 $[n/2+1, n]$ 小的元素。

那么我们只需要维护大根堆的数量为 $n/2$ ，即可知道当前序列的中位数为小根堆的堆顶。

每次我们插入一个数字，如果这个数字比中位数小，则插入大根堆里，否则插入小根堆里。

每当我们插入一个数字，如果大根堆的数量大于 $n / 2$ ，那么把大根堆的最大元素放到小根堆里（堆顶，这也是我们需要两个不同性质的堆的原因）。反之把小根堆的元素放进大根堆里。

Code

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int main ()
{
    int T; cin >> T; while( T -- )
    {
        priority_queue<int, vector<int>, less<int> > pre;
        priority_queue<int, vector<int>, greater<int> > post;
        int id, n, write = 0; cin >> id >> n;
        cout << id << ' ' << (n + 1) / 2 << endl;
        for (int i = 1, x; i <= n && cin >> x; i ++ )
        {
            if (post.empty() || x >= post.top())
            {
                post.push(x);
                if (post.size() - pre.size() > 1)
                {
                    pre.push(post.top());
                    post.pop();
                }
            }
            else
            {
                pre.push(x);
                if (pre.size() > post.size())
                {
                    post.push(pre.top());
                    pre.pop();
                }
            }
            if (i & 1) cout << post.top() << " \n" [++ write % 10 == 0];
        }
        if (write % 10) cout << endl;
    }
    return 0;
}

黑匣子

题意

有两种操作：

1. 向序列中插入一个数字。
2. 求出序列中第 $k$ 小的数字。

$k$ 初始为 $0$ ，每次求第 $k$ 小值都要把 $k$ 加一。

分析

对顶堆，大根堆维护前 $k-1$ 小的数字，小根堆维护后面的数字。这样小根堆的堆顶就是第 $k$ 小的数字。

每次插入操作都至多交换一次堆元素，我们可以放到查询的时候再维护堆的数字，次数与每次操作维护是一样的。

Code

#include <bits/stdc++.h>
using namespace std;

const int N = 200010;

int a[N], q[N], k;

void solve ()
{
    int n, m; cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= m; i ++ ) cin >> q[i];
    int pos = 1;
    priority_queue<int, vector<int>, less<int> > pre;
    priority_queue<int, vector<int>, greater<int> > post;
    for (int i = 1; i <= n; i ++ )
    {
        if (post.empty() || a[i] < post.top()) pre.push(a[i]);
        else post.push(a[i]);

        // 维护post堆顶为k小数
        while (q[pos] == i)
        {
            ++ k;
            while(pre.size() < k) pre.push(post.top()), post.pop();
            while(pre.size() >= k) post.push(pre.top()), pre.pop();
            cout << post.top() << endl;
            pos ++ ;
        }
    }
}

signed main ()
{
    cout.tie(0)->sync_with_stdio(false);
    // int _; for (cin >> _; _ --; ) solve();
    solve();
    return 0;
}