最近公共祖先(LCA)
最近公共祖先 (LCA)
在一个有根树中，两个结点 \(a、b\) 都有若干个祖先(本身也是自己的祖先)，他们也会有公共的祖先，距离他们最近，也就是在有根树中深度最大的祖先，被称做 \(a、b\) 的最近公共祖先。
求最近公共祖先
向上标记法
先从一个点开始向上走到根节点，再由另一个结点开始向上走，走到一个已经被标记过的结点，那么这个结点就是这两个点的最近公共祖先。
最坏情况下树为一条链，时间复杂度为 \(O(n)\) 。
由于复杂度比较大，因此这个算法不常用。
倍增法
倍增法基于二进制拆分，每次都尽可能向上多跳几步。
\(\displaystyle {fa(i, j})\) 表示结点 \(i\) 向上走 \(2^j\) 次后到达的结点。
\(depth(i)\) 表示结点 \(i\) 在有根树中的深度。
对于结点 \(a 、 b\) ，假设 \(depth(a) < depth(b)\) ，我们先把 \(a\) 跳到与 \(b\) 相同的深度；如果此时 \(a == b\) ，那么LCA就是 \(y\) ；否则，我们同时让 \(a、b\) 向上跳到不是 LCA 的结点，最后跳到的结点的父节点就是 LCA 。
由于每次跳的步数都是 \(2\) 的整数次幂，所以时间复杂度为 \(O (log n)\) 。
预处理出所有 \(fa(i, j)\) 的时间复杂度为 \(O (n log n)\) ，所以倍增法适用于多次查询LCA。
例题：洛谷 P3379
#include <bits/stdc++.h>
using namespace std;
const int N = 500010, M = N << 1;
int n, qus, root;
int fa[N][20]; // fa(i, j) 表示i结点向上走 2^j 步到达的结点
int depth[N];
int q[N]; bool st[N]; // BFS
int h[N], e[M], ne[M], idx;
void add (int a, int b)
{
e[idx] = b; ne[idx] = h[a]; h[a] = idx ++ ;
}
void bfs ()
{
int hh = 0, tt = 0;
q[0] = root;
st[root] = true; depth[root] = 1;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i] )
{
int j = e[i];
if (!st[j])
{
st[j] = true;
depth[j] = depth[t] + 1;
q[++ tt] = j;
fa[j][0] = t; // 初始化 fa(i, 0) 为父节点
}
}
}
// 预处理 fa 数组
for (int j = 1; j < 20; ++ j )
for (int i = 1; i <= n; ++ i )
fa[i][j] = fa[fa[i][j-1]][j-1];
}
// 返回 (a, b) 的lca
int lca (int a, int b)
{
if (depth[a] < depth[b]) swap(a, b); // 保证 a 的深度大于 b
// a 跳到与 b 相同深度的结点
for (int i = 19; i >= 0; -- i )
if (depth[fa[a][i]] >= depth[b])
a = fa[a][i];
if (a == b) return b; // a == b ，那么 b 就是 lca
// 同时跳上面
for (int i = 19; i >= 0; -- i )
if (fa[a][i] != fa[b][i])
{
a = fa[a][i];
b = fa[b][i];
}
return fa[a][0]; // 此时 a 父节点就算 lca
}
int main ()
{
cin >> n >> qus >> root;
memset(h, -1, sizeof h);
for (int i = 1; i < n; ++ i )
{
int x, y; cin >> x >> y;
add (x, y); add (y, x);
}
bfs (); // 求出每个结点的深度及fa数组
while (qus -- )
{
int x, y; cin >> x >> y;
cout << lca (x, y) << endl;
}
return 0;
}
Tarjan离线算法
Tarjan算法基于深度优先遍历，本质上是对向上标记法的优化。
遍历有根树，给每个结点分为三类。
- 已经遍历过并且已经回溯的点
- 正在被遍历的点
- 还没有被搜索过的点
当一个结点回溯，我们将它合并到它的父节点上，我们可以发现，如果一次查询包括当前正在被遍历的结点和已经回溯的结点，那么他们的 LCA 就是已经回溯的点所在的集合的祖先结点。而合并及查询集合祖先的操作可以使用并查集。
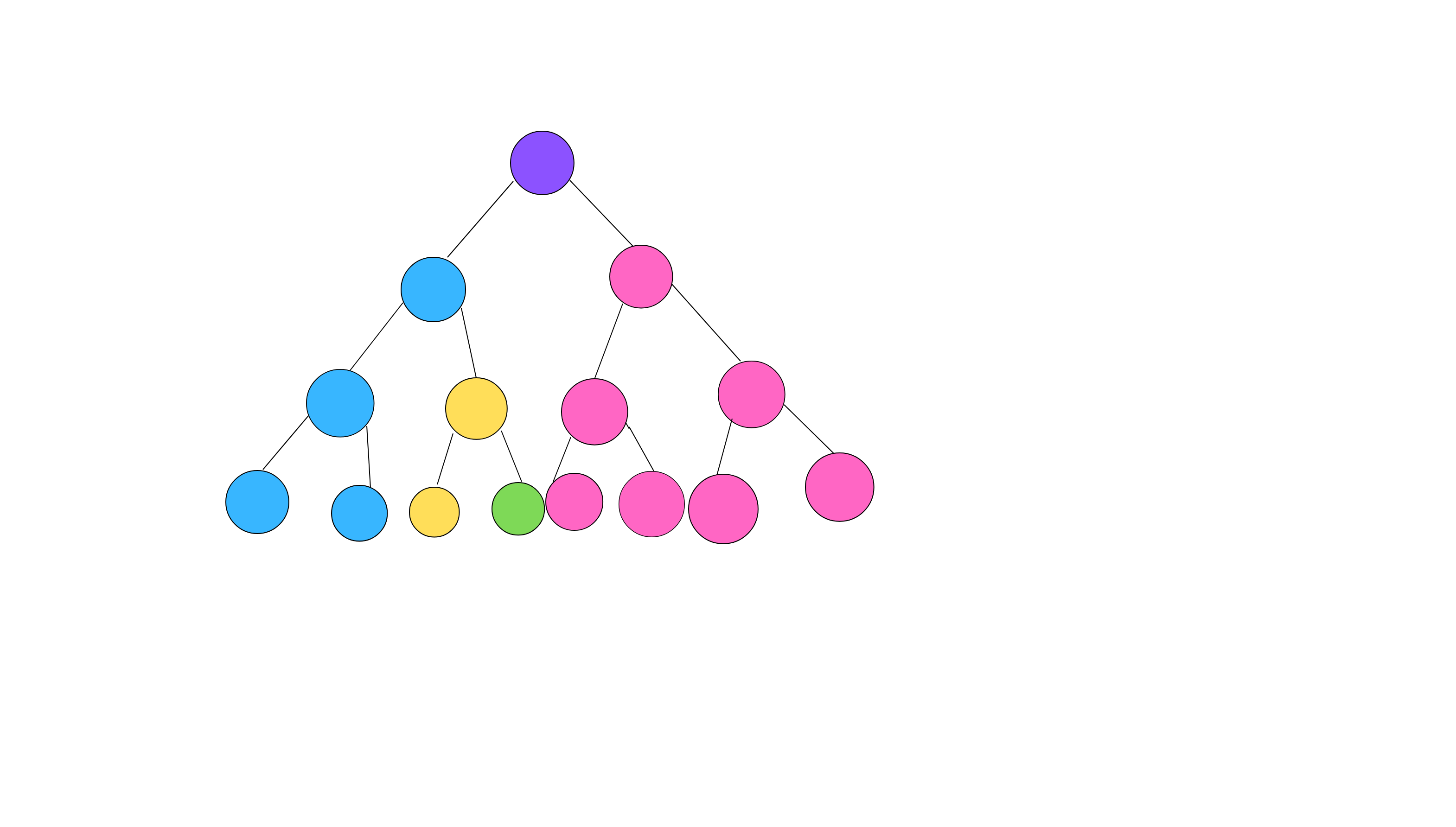
如图，粉色是未被搜索到的点，蓝色是正在被遍历的点，其他都是已经遍历的点(有些未回溯，所以他们处于不同的集合)。
绿色和黄色任意点的LCA都是黄色点集合的祖先结点，其他也是如此。
例题：洛谷 P3379
#include <bits/stdc++.h>
using namespace std;
const int N = 500010, M = N << 1;
typedef pair<int, int> PII ;
int n, qus, root;
int p[N];
int st[N]; // 记录每个点的状态：1表示正在搜索，2表示已经回溯，0表示还没有搜索到
vector<PII> query[N]; // query[i] -> (j, id) 表示在第id个查询中，查询的结点是(i, j)
int ans[N]; // 存储每个查询的结果
int h[N], e[M], ne[M], idx;
void add (int a, int b)
{
e[idx] = b; ne[idx] = h[a]; h[a] = idx ++ ;
}
int find (int x)
{
return p[x] == x ? x : p[x] = find(p[x]);
}
void tarjan (int u)
{
st[u] = 1; // 正在搜索 u 结点
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
// 如果还没有遍历，则遍历子结点
if (!st[j]) { tarjan(j); p[j] = u; } // 回溯后记得及时合并到父节点上
}
for (auto t : query[u])
{
int y = t.first, id = t.second;
if (st[y] == 2) ans[id] = find(y); // 如果j已经回溯
}
st[u] = 2; // u 结点回溯
}
int main ()
{
cin >> n >> qus >> root;
memset(h, -1, sizeof h);
for (int i = 1; i < n; ++ i )
{
int x, y; cin >> x >> y;
add (x, y); add (y, x);
}
for (int i = 1; i <= qus; ++ i )
{
int x, y; cin >> x >> y;
if (x != y)
{
query[x].push_back({y, i});
query[y].push_back({x, i});
}
}
for (int i = 1; i <= n; ++ i ) p[i] = i;
tarjan(root);
for (int i = 1; i <= n; ++ i ) cout << ans[i] << endl;
return 0;
}
