牛客小白月赛36
牛客小白月赛36
链接:https://ac.nowcoder.com/acm/contest/11213
A. 好哥哥
题目描述:
给定一段合法括号序列和\(n\)元钱,合法括号序列的定义如下:
\(()\)是合法的括号序列。
若字符串\(A\)是合法的括号序列,那么\((A)\)也是合法的括号序列。
若字符串\(A,B\)是合法的括号序列,那么\(AB\)也是合法的括号序列。
我们设定\(G_x\)表示第\(x\)对括号的层数,即:它前面有多少未匹配的左括号。同时规定一对括号\(A\)是另一对括号\(B\)的好哥哥,当且仅当\(G_A = G_B + 1\)且括号\(A\)在括号\(B\)内。
如果当前位于一对括号\(Q\),每次可以花费\(1\)元跳到:
它的任意一个好哥哥。
一对括号\(X\),要求\(X\)的好哥哥是\(Q\)。
假如一开始位于第一对括号,请问最多可以经过多少对不重复的括号?
对于每个括号,都有若干个好哥哥,同时它也是至多一个括号的好哥哥,这样的关系可以想到树的结构(其实是看了题解才知道的)。
对于每个括号,向它的好哥哥连一条边,形成一个树,如下图。
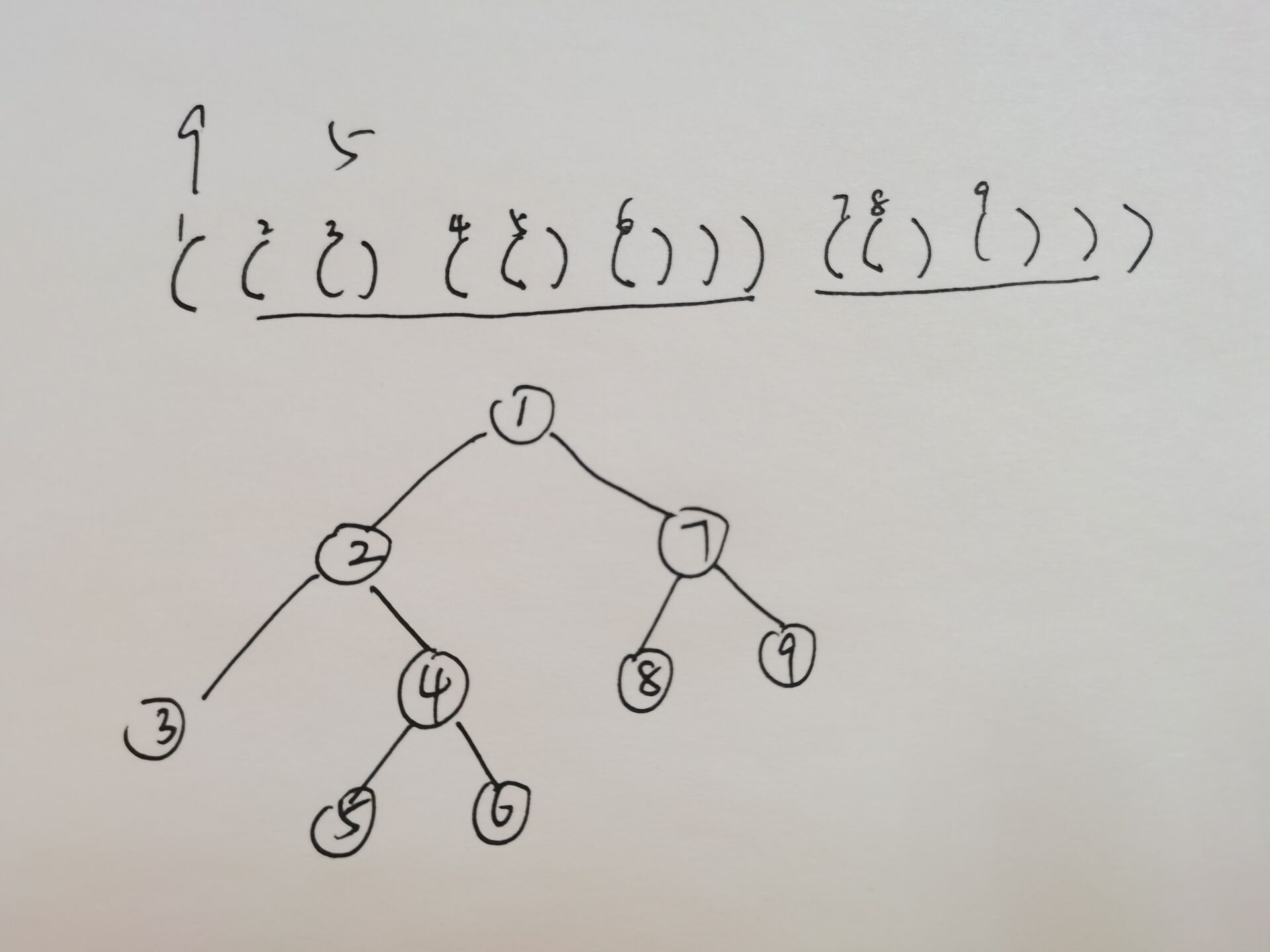
一开始我们在1号括号,很清楚地发现(不是),我们只需要花费1代价就可以直接到好哥哥(走一条边),而到达其他结点,最少只需要花费两个代价,如上图,先走非最长链,再走最长链,这样重复边需要2代价,不重复只需要1代价,根据总代价和最长链的比较即可得出答案。
如上图,1-7-8-7-9-7-1-2-3-2-4-5-4-6
#include <iostream>
#include <string>
using namespace std;
int n, m; // 总括号个数、总代价
string s; // 括号序列
int main () {
int dep = 0; // 树的最大深度
int tot = 0; // 树的总结点个数
cin >> n >> m >> s;
for (int i = 0, left = 0; i < s.length(); i++) {
if (s[i] == '(') left ++, tot ++;
else left --;
if (!left) break; // 以及找到第一个括号
dep = max(dep, left);
}
if (m + 1 <= dep) cout << m + 1 << endl;
else cout << min(tot, dep + (m - dep + 1) / 2);
return 0;
}
B. 最短串
题目描述: 给定两个由小写字母和问号组成的a、b字符串,问号可以表示任意字符。
请找出最短的字符串s,满足s包含a和b两个字符串,输出s的长度。
暴力枚举,先判断小串是否是大串的子串,是则输出大串的长度,否则找出以a为前缀、b为后缀的公共子串长度len1和以b为前缀、a为后缀的公共子串长度len2,最短s即是len(a) + len(b) - max(len1, len2)。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5005;
char a[N], b[N];
int la, lb;
int main () {
cin >> (a + 1) >> (b + 1);
la = strlen(a + 1); lb = strlen(b + 1);
// 是否是子集
if (la < lb)
for (int i = 1, ok = 1; i <= lb; i++, ok = 1) {
for (int j = 1, li = i; j <= la && ok; j++, li++)
if (a[j] != b[li] && a[j] != '?' && b[li] != '?') ok = 0;
if (ok) { cout << lb << endl; return 0; }
}
else
for (int i = 1, ok = 1; i <= la; i++, ok = 1) {
for (int j = 1, li = i; j <= lb && ok; j++, li++)
if (a[li] != b[j] && a[li] != '?' && b[j] != '?') ok = 0;
if (ok) { cout << la << endl; return 0; }
}
// 不是子集,找最大len1和len2
int ans = la + lb; // 最坏情况
// 枚举max(len1, len2)
int i;
for (int t = min(la, lb); t >= 1; t --) {
bool f = 0; // 没找到公共长度为t的串
for (i = 1; i <= t; i++)
if (b[i] != a[la - t + i] && b[i] != '?' && a[la - t + i] != '?') break;
if (i > t) f = true;
for (i = 1; i <= t; i++)
if (a[i] != b[lb - t + i] && a[i] != '?' && b[lb - t + i] != '?') break;
if (i > t) f = true;
if (f) ans = min(la + lb - t, ans);
}
cout << ans << endl;
}
C.杨辉三角(组合数学)
题目描述: 小F对杨辉三角颇有研究,他把杨辉三角第n行的数提取出来,从左到右依次为:a[0],a[1],....,a[n-1]。现在他想要知道\(\sum_{i=0}^{n-1}i^2 * a[i]\)的值为多少,答案对99824353取模。
输入描述:
输入一个正整数n,n \(\leq\) 1018。
先转化到从0行开始算(结论更强,0更好算)。

如图可以得出结论。
#include <iostream>
using namespace std;
typedef long long LL;
const int mod = 99824353;
int quick_pow (LL k) {
int ans = 1, base = 2;
while (k) {
if (k & 1) ans = (LL)ans * base % mod;
base = (LL)base * base % mod;
k >>= 1;
}
return ans;
}
int main () {
LL n;
cin >> n;
-- n; // 从第0行开始算
if (n == 0) cout << 0 << endl;
else if (n == 1) cout << 1 << endl;
else cout << ((LL)quick_pow(n - 2) * (n + 1) % mod * n % mod) << endl;
return 0;
}
D.哥三好(DP)
题目描述:
正所谓三人成行,阿猫、阿狗、阿猪三兄弟又到了一年一度的已婚男人单身日,他们每年都会相聚网咖门口准备包夜。
已知他们三每人都有一个偷偷藏起来的小金库,都是为了在这一年一度的日子中发挥作用。这哥三都觉得请客的时候贼有面子,所以都会抢着请客,即其中一人一次性买三个人的单。已知该网吧的电脑分为三个价位,分别为100元,150元,250元每晚/人,每次他们都会定三台价位相同的电脑进行包夜。
假设这三兄弟往后都不会往这个小金库藏钱,而且小金库的钱只会用来网吧包夜。请问在给定三个人小金库存钱量的情况下,如果将每年的请客情况记录下来,直到他们花到他们三全部都去不起网吧的时候,有多少种不同的请客记录。规定只要中间有一年请客的人不同或者请客的电脑价位不同即算不同,最终答案对1000000007取模。
动态规划,设f(i, j, k)表示三人金库为i, j, k时的请客记录,那么转移方程是:,转移方程太长了,直接看代码。
这里由于每次请客耗费的价钱都是150的倍数,可以除以150表示价位,减少空间复杂度。
时间复杂度:\(O((a/150) \times (b/150) \times (c/150))\)。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 120, mod = 1000000007;
int f[N][N][N]; // f(i, j, k)表示三人金库为i, j, k时的请客记录
int get (int a, int b, int c) {
// 都请不起客,也是一种方案
if (a < 2 && b < 2 && c < 2) return 1;
int & ans = f[a][b][c];
if (ans != -1) return ans;
ans = 0;
// 请2价位
if (a >= 2) ans = (ans + get(a - 2, b, c)) % mod;
if (b >= 2) ans = (ans + get(a, b - 2, c)) % mod;
if (c >= 2) ans = (ans + get(a, b, c - 2)) % mod;
// 请3价位
if (a >= 3) ans = (ans + get(a - 3, b, c)) % mod;
if (b >= 3) ans = (ans + get(a, b - 3, c)) % mod;
if (c >= 3) ans = (ans + get(a, b, c - 3)) % mod;
// 请5价位
if (a >= 5) ans = (ans + get(a - 5, b, c)) % mod;
if (b >= 5) ans = (ans + get(a, b - 5, c)) % mod;
if (c >= 5) ans = (ans + get(a, b, c - 5)) % mod;
return ans % mod;
}
int main () {
int a, b, c;
cin >> a >> b >> c;
a /= 150; b /= 150; c /= 150;
memset(f, -1, sizeof f);
cout << get(a, b, c) << endl;
return 0;
}
E. 皇城PK
题目描述:有n名选手会进行m次比赛,每次比赛不会出现平局的情况,只有一个胜者。在每次比赛完成之后,我们视胜者选手的实力比败者选手实力强,如果出现选手A打败选手B,选手B打败选手C,选手C打败选手A,则视为他们的实力一样。
若该赛季最终冠军是属于实力最强者,请问依照现在已有的比赛结果,最多有多少个选手可能获得冠军(如果已知两个选手的实力一样强,那么两个人都不能获得冠军)。
输入描述:
第一行输入两个正整数n,m,其中:n \(\leq\) 105,m \(\leq\) 105。
接下来m行,每行两个正整数a与b,代表选手a战胜了选手b,满足:a \(\leq\) n, b \(\leq\) n。
输出描述:
输出最多有多少名选手可能成为冠军。
签到题,如果一个人失败了,那么他就不可能成为冠军(总有人比他实力更强),只需要找出有多少人失败了,就能知道有多少名选手可能成为冠军。
#include <iostream>
#include <set>
using namespace std;
int main () {
set<int> defeat;
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y; cin >> x >> y;
defeat.insert(y);
}
cout << n - defeat.size() << endl;
return 0;
}
F. 象棋
题目描述: 给定一个n \(\times\) m的棋盘,全部摆满炮,假设所有炮都属于不同阵营,请问他们互相攻击后,最少剩下几个炮。
思维题,对于大于等于\(2 \times 1\)的棋盘,我们可以用最上面两行炮,把下面所有炮打掉,而对于剩下来的两行炮,每行最多剩下两个炮(反证)。
#include <iostream>
using namespace std;
int main () {
int T; cin >> T;
while ( T -- ) {
long long n, m; cin >> n >> m;
if (n <= 2 && m <= 2) printf("%d\n", n * m);
else if (n == 1 && m >= 2 || m == 1 && n >= 2) printf("2\n");
else printf("4\n");
}
return 0;
}
G. 永不言弃
题目描述:
小沙最喜欢打怪升级了,今天他玩了一个游戏,需要从初始关卡开始,击败n个关卡才能通关整个游戏,对于每个关卡都会有两种通过方式。
小沙初始的属性值为s,当游戏角色的属性大于关卡最高上限时,可以强行通过该关卡,又或者拥有通过该关卡的必过道具(并不是消耗品)。每个关卡通过后可能会开启一个或多个后置关卡,但每个关卡开启也需要若干个前置关卡,只有前置关卡全部通过后,才能开启该关卡。特别注意,除了一号关卡,如果一个关卡没有任何前置关卡,那么这个关卡则永远无法开启。
每个关卡仅能游玩一次,且每个关卡通过都会增强小沙角色的属性,也会给予一个必过道具。目前小沙正在一号关卡,请问小沙能否将这个游戏打通。
输入描述:
第一行输入两个正整数\(n,s\),其中:\(n \leq 5 \times\) \(10^4\) ,\(s \leq 100\)。
接下来\(n\)行,每行输入两个正整数\(a_i, b_i\),分别代表第\(i\)关暴力通过需要的属性值,以及该关卡所需的必过道具,其中:\(a_i\leq10^6,b_i\leq n\)。
接下来\(n\)行,每行输入两个正整数\(c_i,b_i\),分别代表通过第\(i\)关后,可以增加的属性值,以及可以获得的必过道具,其中:\(c_i \leq 10^6,d_i \leq n\)。
接下来\(n\)行,每行首先输入一个非负整数\(k\),代表有多少个后置关卡,随后\(k\)个整数代表第\(i\)关的后置关卡。其中:\(k\leq 10\),后置关卡号小于等于\(n\)。
不会写,看了题解才明白,是一道拓扑排列\(+\)BFS的题目。
画张图应该就明白了。

根据常识,我们打关卡一定是一步步从简单到难,慢慢提升属性才能挑战更难的关卡,所以我们要按照优先队列,把每个关卡的暴力通关值升序排列,开始扫描即可。
由于这题有必需品,打通关了这个关卡,我们就可以把获得的道具,对相应的关卡的暴力通关值设置无穷小(因为可以不用暴力直接过)。
#include <iostream>
#include <queue>
#include <vector>
#include <cstring>
using namespace std;
const int N = 50010, M = 500010;
typedef pair<int, int> PII;
int n, s; // 通过关卡累加属性值
int force[N]; // 暴力通过第i关卡需要的属性
int add[N]; // 通过第i关增加的属性值
int acquire[N]; // 通过第i关能获得的物品
bool st[N]; // i关卡是否已经被通关
vector<int> pre[N]; // 用i物品能够通过的关卡
/* 拓扑图,邻接表存放 */
int h[N], e[M], ne[M], idx;
int in[N]; // 结点的入度
void add_edge (int a, int b) {
e[idx] = b; ne[idx] = h[a]; h[a] = idx ++;
}
bool bfs () {
priority_queue<PII, vector<PII>, greater<PII> > q;
q.push({force[1], 1});
// 除了1号关卡,其他如果没有前置关卡,永远无法打开,直接return false
for (int i = 2; i <= n; i++) if (!in[i]) return false;
while (q.size()) {
auto t = q.top(); q.pop();
int _force = t.first, now = t.second;
if (st[now]) continue; // 已经通过过了
if (s > _force) {
s += add[now];
st[now] = true;
// 删前置边
for (int i = h[now]; ~i; i = ne[i]) {
int ver = e[i];
if (-- in[ver] == 0) q.push({force[ver], ver});
}
// 获得物品, 有些关卡不需要暴力
for (auto & c : pre[acquire[now]]) {
/*
一开始这样写AC了,但有数据可以Hack,因为虽然不需要暴力,但这个关卡可能还有前置边,不能直接加入队列。
q.push({-1, c});
*/
force[c] = -1;
if (!in[c]) q.push({-1, c});
}
}
}
// 所有的关卡都要通过
for (int i = 1; i <= n; i++) if (!st[i]) return false;
return true;
}
int main () {
cin >> n >> s;
// 暴力值、需要的必须物品
for (int i = 1; i <= n; i++) {
int need;
cin >> force[i] >> need;
pre[need].push_back(i);
}
// 增加的属性值、获得的物品
for (int i = 1; i <= n; i++) {
cin >> add[i] >> acquire[i];
}
// 后置关卡
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i++) {
int k; cin >> k;
for (int j = 1; j <= k; j++) {
int post; cin >> post;
add_edge(i, post);
in[post] ++;
}
}
puts(bfs() ? "Yes" : "No");
return 0;
}
H. 卷王之王
题目描述:给定一个n个数字的序列以及m次操作,每次操作把序列中小于等于给定值x的数字加上x,输出最后的序列。
输入范围
第一行n, m两个数字,n, m \(\leq\) 105。
第二行n个非负整数a[i],a[i] \(\leq\) 109。
接下来m行,每行一个非负整数x,x \(\leq\) 109。
直接暴力复杂度为O(n2),一定会超时。
由于被加的数字一定小于等于x,那么每个数字都是倍增的,也就是最多被加入\(\log x\)次。
我们不需要枚举每个数字,因为只对小于等于x的数字进行操作,可以使用优先队列进行优化。
这样时间复杂度降低为O(n \(\log n\) \(\log x\))。
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int n, m;
priority_queue<PII, vector<PII>, greater<PII> > q;
vector<PII> temp;
int ans[N];
int main () {
scanf("%d%d", &n, &m);
for (int i = 1, x; i <= n; i++) scanf("%d", &x), q.push({x, i});
while ( m -- ) {
int x; scanf("%d", &x);
if (!x) continue;
// a[i]是0的时候会加两次,错误!!
// while (q.top().first <= x) q.push({q.top().first + x, q.top().second}), q.pop();
temp.clear();
while (q.size() && q.top().first <= x) temp.push_back(q.top()), q.pop();
for (auto & item : temp) item.first += x, q.push(item);
}
while (q.size()) ans[q.top().second] = q.top().first, q.pop();
for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
return 0;
}
I.四面楚歌
题目描述:给定一张n \(\times\) m的地图,'.'表示空地,'1'表示敌人, '0'表示友军,求在敌人不移动不攻击的情况下,有多少友军能逃出地图。
最开始想的是多源BFS,后来发现错了,因为一个友军在转移状态时,如果四周有另一个'0',我们并不能判断那个右军是否已经离开这个位置(在这个右军转移状态时是否以及转移过),以及是否有友军到达空地(不能占用同一块)。
看了一下题解,发现用的是DFS找能出地图的连通块,染色,最后找出染色后的块有几个友军(没想到....)。
后来问队友,发现了一个神奇的解法。
如果一个友军能走出地图,我们假设地图外都是空地,那么他们一定能会合到某个空地,我们假设这个空地为(0, 0),只需要从这个汇点出发,BFS找出能连通的友军即可。
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 1010;
typedef pair<int, int> PII;
const int dr[] = { -1, 1, 0, 0 }, dc[] = { 0, 0, -1, 1 };
int n, m;
char g[N][N];
bool vis[N][N];
bool check (int x, int y) {
return x >= 0 && x <= n + 1 && y >= 0 && y <= m + 1 && !vis[x][y];
}
int bfs () {
int cnt = 0;
queue<PII> q;
q.push({0, 0});
vis[0][0] = true;
while (q.size()) {
auto t = q.front(); q.pop();
int x = t.first, y = t.second;
if (g[x][y] == '0') cnt++;
for (int i = 0; i < 4; i++) {
int dx = x + dr[i], dy = y + dc[i];
if (check(dx, dy) && (g[dx][dy] == '.' || g[dx][dy] == '0' || g[dx][dy] == 0)) {
vis[dx][dy] = true;
q.push({dx, dy});
}
}
}
return cnt;
}
int main () {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> (g[i] + 1);
cout << bfs() << endl;
return 0;
}
J. 科学幻想
题目描述:
给定一个字符串s(长度n),进行m次操作,操作有如下两种。
把字符串第x个字符修改为y。
询问\([l1, r1]\)区间的字符串与\([l2,r2]\)区间的字符串是否勉强相等。
勉强相等:区间长度相等,且对应位置上至多一个位置的字符不同,则这两个字符串勉强相等。
对于每次操作2,如果勉强相等,输出“YES”,否则输出“NO”。
线段树+字符串Hash+二分
对于2操作,查询相等我们可以用字符串Hash来判定,可是这道题至多有1个不相等字符,我们可以用二分来做。
把两个区间每个分成不同的两个区间,若对应两个区间Hash均不相等,则两个区间都存在不相等字符,那么肯定不满足勉强相等的条件。如果仅有1个不相等,那么我们只需要在这个区间继续判断即可。
至于1操作,由于数据太大,暴力修改会重新计算每个区间Hash,肯定超时,这里可以使用线段树来维护区间Hash。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
typedef unsigned long long ULL;
const int N = 100005, P = 13331; // 字符串Hash的P值
int n, m;
char str[N];
/* segment tree 存hash */
ULL _hash[N << 2], pw[N];
void build (int p, int l, int r) {
if (l == r) {
_hash[p] = str[l]; return;
}
int mid = l + r >> 1;
build(p<<1, l, mid);
build(p<<1|1, mid+1, r);
_hash[p] = pw[r - mid] * _hash[p<<1] + _hash[p<<1|1];
}
void update (int p, int l, int r, int pos, char chg) {
if (pos == l && l == r) {
_hash[p] = chg;
return;
}
int mid = l + r >> 1;
if (pos <= mid) update(p<<1, l, mid, pos, chg);
else update(p<<1|1, mid+1, r, pos, chg);
_hash[p] = pw[r - mid] * _hash[p<<1] + _hash[p<<1|1];
}
// 返回(l, r)范围字符串的hash值
ULL get_hash (int p, int L, int R, int l, int r) {
if (l <= L && r >= R) return _hash[p];
int mid = L + R >> 1;
if (l > mid) return get_hash(p<<1|1, mid+1, R, l, r);
if (r <= mid) return get_hash(p<<1, L, mid, l, r);
return pw[r - mid] * get_hash(p<<1, L, mid, l, mid) + get_hash(p<<1|1, mid+1, R, mid+1, r);
}
int main () {
cin >> n >> m >> (str + 1);
pw[0] = 1;
for (int i = 1; i < N; i++) pw[i] = pw[i - 1] * P;
build(1, 1, n);
while (m --) {
int op; cin >> op;
if (op == 1) {
int x; char y; cin >> x >> y;
update(1, 1, n, x, y);
}
else {
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
if (r1 - l1 != r2 - l2) {
puts("NO");
continue;
}
// 二分判断hash值
// 两个串长度相同,二分成两段
int ll = 1, rr = r1 - l1; // 二分左侧长度
bool f = true;
while (ll <= rr) {
int mid = ll + rr >> 1;
ULL t1 = get_hash(1, 1, n, l1, l1 + mid - 1), t2 = get_hash(1, 1, n, l1 + mid, r1);
ULL t3 = get_hash(1, 1, n, l2, l2 + mid - 1), t4 = get_hash(1, 1, n, l2 + mid, r2);
if (t1 == t3 && t2 == t4) break;
if (t1 != t3 && t2 != t4) { f = false; break; }
if (t1 != t3) rr = mid - 1;
else ll = mid + 1;
}
puts(f ? "YES" : "NO");
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号