二分法

二分法

二分法有两种，二分查找和二分答案。

二分查找

整数二分

整数二分的实质不在于单调性，而是看区间能否划分为两块，使得一块满足某种性质，而另一块不满足。

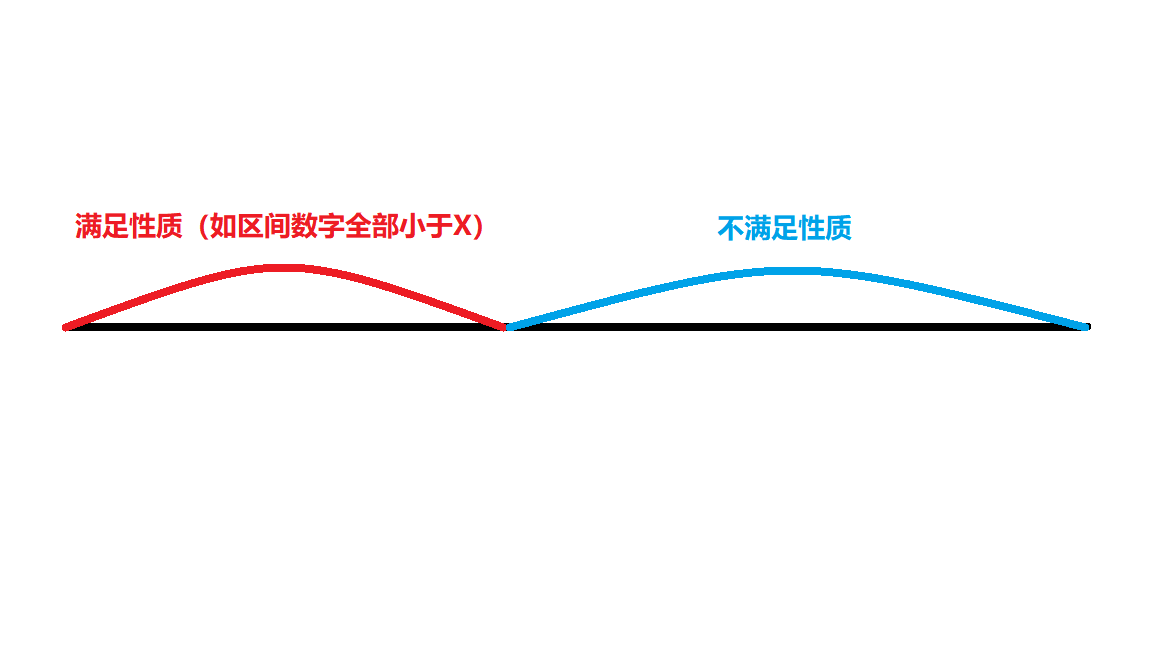
1.查找红色区域最后的值(满足条件的最后一个值)：

​ check(mid):

1. true  -> [mid, R];  --- l = mid
2. false -> [L, mid - 1]; --- r = mid - 1

2.查找蓝色区域第一个值(满足条件的第一个值):

​ check(mid):

1. true -> [L, mid]; --- r = mid
2. false -> [mid + 1, R]; --- l = mid + 1

二分查找想不出的话可以画一画图，确定一下两个分段。

二分查找模板:

bool check (int x) {/* ... */} // 检查x是否满足某个条件

// 区间[l, r]被划分为[l, mid]和[mid+1, r]:(满足条件的第一个元素)
int bsearch_1 (int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

// 区间[l, r]被划分为[l, mid-1]和[mid, r]:(满足条件的最后一个元素)
int bsearch_2 (int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

浮点数二分

bool check (double x) {/* ... */} // 检查x是否满足某个条件

double bsearch_3 (double l, double r) {
    const double eps = 1e-6; // eps表示精度，取决于题目的精度要求
    while (r - l > eps) {
        double mid = r + l >> 1;
        if (check(mid)) r = mid; // r和l可互换，取决于题目要求
        else l = mid;
    }
    return l;
}

二分答案

根据答案的单调性（可满足性）把答案所取范围二分，每次取中间判断是否可以满足题目要求，满足则记录当前数值，直至二分完毕，则记录的值为二分答案值。

例题：

数的三次方根