EOJ Monthly 2020.3 A.迷宫 （二分+最大流）

题目链接

https://acm.ecnu.edu.cn/contest/255/problem/A/

题意

给出有向图，有\(m\)个人在顶点\(S\)，每天晚上你可以控制他们呆在原地不动或选择移动到下一个顶点（从一个顶点到相邻顶点恰好需要花费一个晚上时间），当然，你可以控制每一个青年有不一样的选择。每条边都有一个容量\(C\)，代表着在同一个晚上最多\(C\) 个人可以穿过该边。
现在要求你在最少的时间内帮助所有人到达迷宫的出口\(T\)
保证给出的图，至少存在一条路径能从\(S\)到\(T\) 。

思路

官方题解：
考虑二分答案。
我们现在要判断，所有人能否在\(mid\)天内走出去。
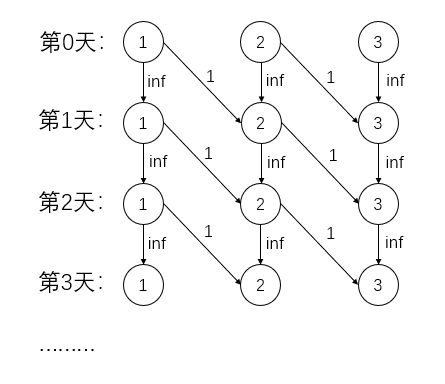
因为道路限制了每天通过的流量，我们不妨拆点，分层建图，把每一个点拆成 (标号，天数) 在相邻节点相邻的天数之间连边，然后跑最大流就好了。
比如样例的图我们这样去建：

#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int N = 5100;
const int M = 2e6+10;
struct node{int u,v,w;}a[N];
struct edge{int to,cap,next;}e[M];
int head[N],tot;
int d[N],cur[N];
int k,n,m,S,T,s,t;
void add(int u,int v,int w)
{
    e[++tot].to=v,e[tot].cap=w;
    e[tot].next=head[u],head[u]=tot;
}
bool Bfs()
{
	memset(d,0,sizeof(d));
	queue<int>q;
	q.push(s);
	d[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=-1;i=e[i].next)
		{
			int v=e[i].to;
			if(!d[v]&&e[i].cap)
			{
				d[v]=d[u]+1;
				q.push(v);
			}
		}
	}
	return d[t];
}
int Dfs(int u,int flow)
{
	if(u==t||!flow) return flow;
	int used=0;
	for(int i=cur[u];i!=-1;i=e[i].next)
	{
		cur[u]=i;
		int v=e[i].to;
		if(d[v]==d[u]+1&&e[i].cap)
		{
			int fl=Dfs(v,min(flow,e[i].cap));
			if(fl)
			{
				used+=fl;
				flow-=fl;
				e[i].cap-=fl;
				e[i^1].cap+=fl;
				if(!flow) break;
			}
		}
	}
	return used;
}
int Dinic()
{
	int sum=0;
	while(Bfs())
	{
		memcpy(cur,head,sizeof(head));
		sum+=Dfs(s,inf);
	}
	return sum;
}
bool judge(int x)
{
    tot=-1;
    memset(head,-1,sizeof(head));
    for(int i=1;i<=m;i++)
    {
        int u=a[i].u,v=a[i].v,w=a[i].w;
        for(int j=0;j<x;j++)
            add(u+j*n,v+(j+1)*n,w),add(v+(j+1)*n,u+j*n,0);
    }
    for(int i=1;i<=n;i++)
        for(int j=0;j<x;j++)
            add(i+j*n,i+(j+1)*n,inf),add(i+(j+1)*n,i+j*n,0);
    s=S,t=T+x*n;
    int tmp=Dinic();
    if(tmp>=k)return true;
    else return false;
}
int main()
{
    scanf("%d%d%d%d%d",&k,&n,&m,&S,&T);
    for(int i=1;i<=m;i++)
        scanf("%d%d%d",&a[i].u,&a[i].v,&a[i].w);
    int l=1,r=100,ans;
    while(l<=r)
    {
        int mid=(l+r)/2;
        if(judge(mid))r=mid-1,ans=mid;
        else l=mid+1;
    }
    printf("%d\n",ans);
    return 0;
}