再谈反向传播（Back Propagation）
此前写过一篇《BP算法基本原理推导----《机器学习》笔记》，但是感觉满纸公式，而且没有讲到BP算法的精妙之处，所以找了一些资料，加上自己的理解，再来谈一下BP。如有什么疏漏或者错误的地方，还请大家不吝赐教。
1.泛谈BP
说到反向传播，无非四个字——“链式求导”，但实际上BP不止如此，BP是在这个基础上，加入了一点动态规划的机制。一般的BP包含以下几个步骤：
- 前向传导
- 反向传播梯度计算
在反向传播进行梯度计算的时候，BP不会进行重复计算，其原因就是在前向传导的时候，进行了中间变量的存储，并且在反向传播的时候，可以进行DP。如果现在对这个过程不是很清楚，那么不急，下一节我将用一个例子来直观地说明BP算法的运行流程。
在讲BP时，再啰嗦一下BP的应用场景：
BP算法适用于简化多变量复合求导的过程
机器学习无非就是目标函数$Objective\ function $和一个学习算法，其中学习算法最基本的就是SGD（随机梯度下降），BP就可以用来计算其中的批梯度。
比如下面一个公式：
注：\(\sigma(x)=\frac{1}{1+exp(-x)}\)
如果直接求出\(f(x,y)\)导数的解析解，你会发现这是一个很复杂的表达式，而且如果对多变量的每个变量都用解析的方式求解，那么将会浪费更多的存储空间以及无谓的重复计算。而使用BP，你可以看到一个清爽的求解过程，简单的求解步骤。
2.细说BP
我们使用上一节提出的公式(1)来讲解BP具体是怎么工作的。先来回顾一下公式(1)：
我们使用计算图的模型来表示这个计算过程。
实际上计算图所做的工作就是将原本的复杂表达式分解成中间步骤的聚合。计算图如下：
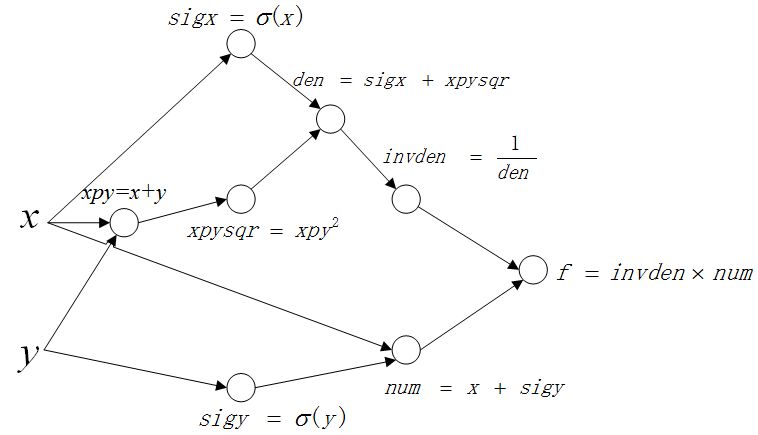
其中每个节点分别表示一个中间步骤，等式的左边表示中间变量，右边表示中间变量的解析表达。可以看到这个聚合的最终结果就是我们的公式(1)。
接下来说明BP怎么根据这个计算图进行梯度计算。
前向传播
根据BP算法步骤，第一步就是前向传播。
前向传播很简单，在传播的过程中，我们保存每一个中间变量的值，也就是每个中间节点的输出值。
反向传播
从输出开始，反向传播梯度值，计算输出值对于每一个中间变量的梯度，并保存，在上图中就是 f。
一层一层来看这个传播过程。
1）第一层
第一层传播图如下(红色箭头表示传播方向)：
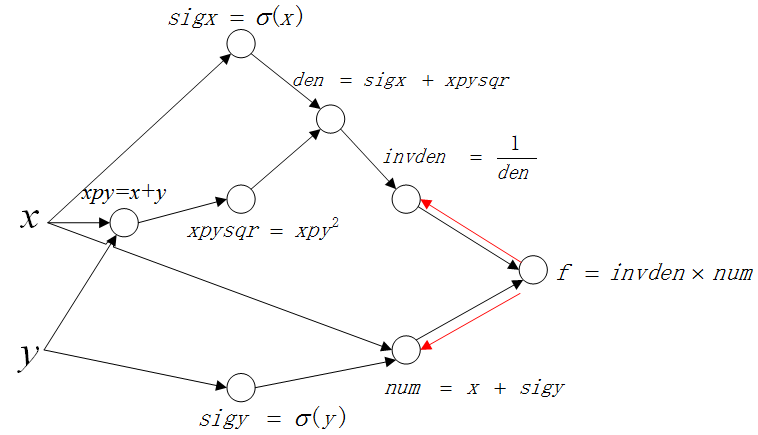
以上面的路线为例：
这里先计算 \(\frac{d(f)}{d(invden)}\)，并保存结果 \(dinvden\)：
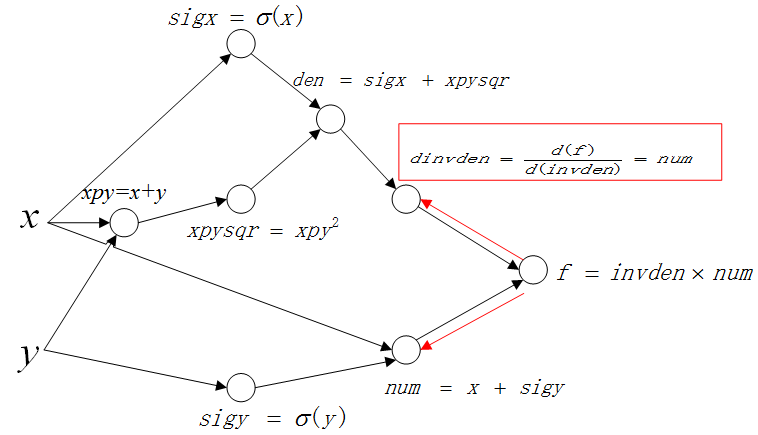
2）第二层
继续以这条路线“反向传播”计算第二层：
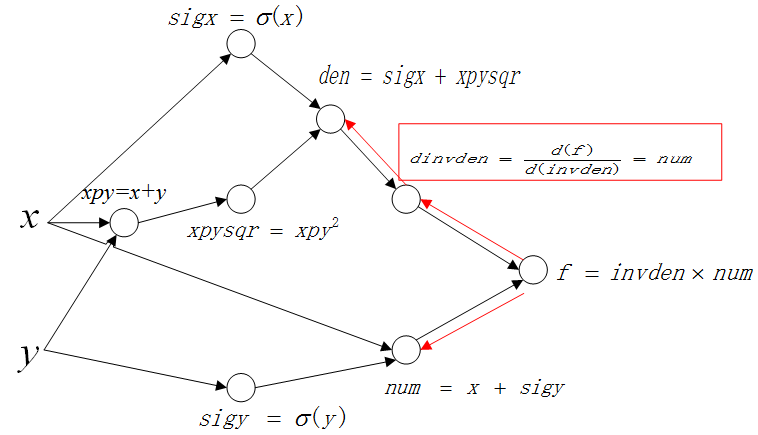
这里要计算 \(\frac{d(f)}{d(den)}\),这里不像第一层一样，可以一次获得结果，因为变量 \(den\) 和 \(f\) 中间隔着一个中间变量 \(invden\),所以需要用到链式法则(这里就是链式求导在BP算法中的运用)。 链式推导如下：
根据原始计算图以及上一步的中间结果：
(2)(3)联立，得：
整个计算过程展示如下：
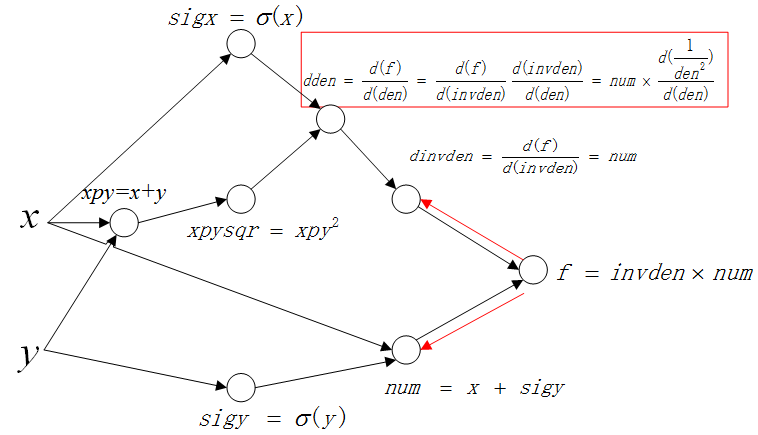
就这样，BP不断地反向传播梯度，并保存中间梯度，直到计算图的所有中间值以及初始值的梯度被求解完毕。
总结
根据以上过程，总结BP算法具体需要以下几个步骤。
- 前向传导
可以注意到，在梯度回传的过程中需要用到节点的输出值，所以在前向传播的过程中需要保存每个节点的输出值。同时，输出值关于输入值的梯度也可以马上获得，这在反向传播的求解中也需要用到。所以前向传导记录以下两个值：- 中间结点的输出值
- 输出值关于输入值的梯度
- 反向传播
反向传播就是一个计算网络最终输出值关于自己输出的梯度的过程。
