BP算法基本原理推导----《机器学习》笔记
前言
多层网络的训练需要一种强大的学习算法，其中BP（errorBackPropagation）算法就是成功的代表，它是迄今最成功的神经网络学习算法。
今天就来探讨下BP算法的原理以及公式推导吧。
神经网络
先来简单介绍一下神经网络，引入基本的计算公式，方便后面推导使用
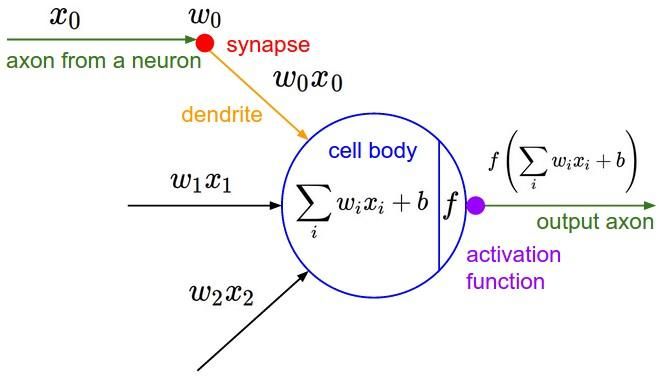
图1 神经网络神经元模型
图1就是一个标准的M-P神经元模型。
【神经元工作流程】
每个神经元接受n个（图1中只有3个）来自其他神经元或者直接输入的输入信号（图1中分别为x0,x1,x2），这些输入信号分别与每条“神经”的权重相乘，并累加输入给当前神经元。每个神经元设定有一个阈值θ（图1中的b），累计值需要减去这个阈值，并且将最终结果通过“激活函数”（图1中的f）挤压到（0,1）范围内，最后输出。
总结一下，神经元的工作流程主要有3步：
①累计输入的信号与权重。
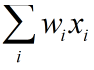
②将权重与设定的阈值相减
③将第2步得出的结果送给激活函数（一般是sigmoid函数），输出
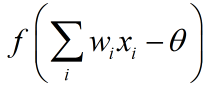
【多层前馈神经网络】
将上面的神经元按照一定的层次结构连接起来，就得到了神经网络。
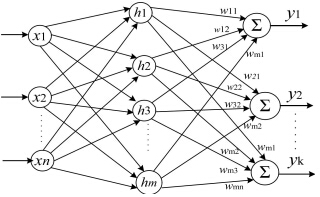
图2 多层前馈神经网络
图2显示的是一个3层（1个输入层，1个隐藏层，1个输出层）的神经网络。
像这样的形成层级结构，每层神经元与下一层神经元全连接（每层的每个神经元到下一层的每个神经元都有连接），神经元之间不存在同层连接，也不存在跨层连接的神经网络通常被称为“多层前馈神经网络”。
【神经网络工作流程】
假定有数据集D:
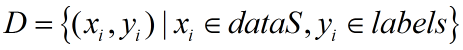
输入神经网络，同样假定就是图2这个3层前馈神经网络，我们来列一下，图2这个网络要通过这些训练集来训练得到多少个参数。
图2的神经网络有n个输入神经元（记为x1、x2....xn）、m个隐藏层神经元（记为h1,h2,...,hm），k个输出神经元（记为y1,y2,...,yk），通过训练，我们要获得下面几种数值
①输入层到隐藏层的权值：n x m 个
②隐藏层到输出层的权值：m x k 个
③m个隐藏层阈值与k个输出层阈值
训练完成后，通过测试集样例与训练出的参数，可以直接得到输出值来判断所属分类（分类问题）
BP算法
神经网络的运行过程清楚了，那么训练过程是怎么样的呢？
我们知道，训练的任务是：
通过某种算法，习得上面所讲的n x m + m x k + m + k = (n+k+1) x m + k 个参数
这里我们使用的就是BP算法。
先来根据神经元工作流程来定义几个量，这里再贴一下修改后的神经网络流程图
图3 3层前馈神经网络图
【定义】
第i个输入神经元到第j个隐藏层神经元的权重:Vij
第i个隐藏层神经元到第j个输出层神经元的权重:Wij
第i个隐藏层神经元的输出：bi
第i个输出层的阈值:θi
第j个隐藏层神经元的输入：
第q个输出神经元的额输入：
假定通过我们的神经网络，对于训练样例
网络输出为
假定完美输出应该为
，例如，对于k分类问题，若训练样例p属于第1类，则yp=(1,0,0,0...,0)
那么一轮训练我们的均方误差为：
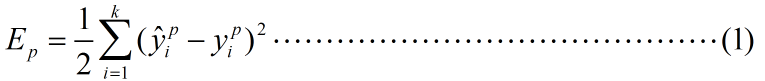
实际上
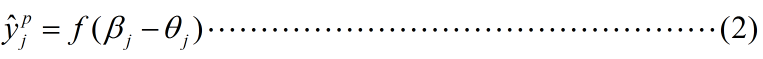
其中f函数为sigmoid函数。
这下，我们的目标就转化为：
寻得一组合适的参数序列，使得(1)式的值（均方误差）最小。
在我的上一篇随笔里也提到过这个问题，这种形式的问题比较适合使用梯度下降算法，BP正是采取了这个策略，以目标的负梯度方向对参数进行调整。
【梯度下降求解参数】
梯度下降的基本思想是：设定参数的初始值，通过一个学习速率η和当前梯度，来逐渐步进参数，以求拟合一个局部最优的参数
一般的参数迭代过程如下：
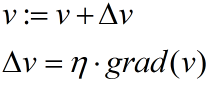
不清楚梯度下降算法的可以看一下我另一篇随笔：http://www.cnblogs.com/HolyShine/p/6403116.html
神经网络的一次迭代，就是参数的一次“步进”。
接下来我们使用梯度下降分别推导几个参数的迭代公式
我们以隐藏层中第h个神经元为参照对象，求解他的输入权重V和输出权重W，以及阈值γ；以输出层中第j个神经元为输出参照，求解他的阈值θ
<隐藏层到输出层的权重Whj>
根据梯度下降算法，权重参数的步进为：
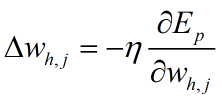
由复合函数求导公式以及式（1）式（2）：
其中，第二项是sigmoid函数求导，由于sigmoid函数有如下的性质：
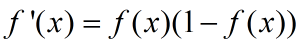
所以
第一项和第三项的推导也列在这里
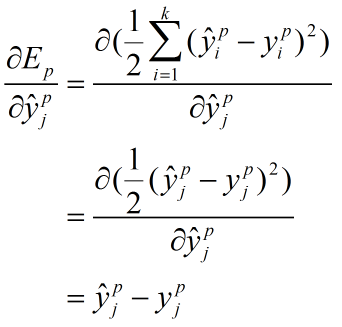
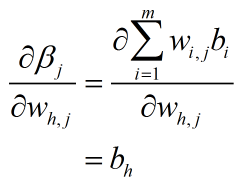
最终（3）式变为：
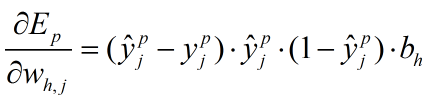
这些量都是一轮训练中已知的，因此可以解得梯度的大小，用于参数的更新工作
其他参数的求解基本一致。
