Logistic回归Cost函数和J(θ)的推导（二）----梯度下降算法求解最小值
前言
在上一篇随笔里，我们讲了Logistic回归cost函数的推导过程。接下来的算法求解使用如下的cost函数形式：
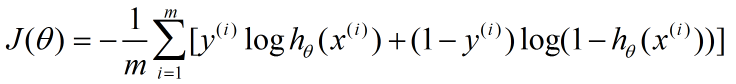
简单回顾一下几个变量的含义：
| x(i) | 每个样本数据点在某一个特征上的值，即特征向量x的某个值 |
| y(i) | 每个样本数据的所属类别标签 |
| m | 样本数据点的个数 |
| hθ(x) | 样本数据的概率密度函数，即某个数据属于1类（二分类问题）的概率 |
| J(θ) | 代价函数，估计样本属于某类的风险程度，越小代表越有可能属于这类 |
我们的目标是求出θ，使得这个代价函数J(θ)的值最小，这里就需要用到梯度下降算法。
梯度下降算法
对于一个函数，我们要找它的最小值，有多种算法，这里我们选择比较容易用代码实现和符合机器学习步骤的梯度下降算法。
先来看看梯度下降算法中，自变量的迭代过程。表示如下
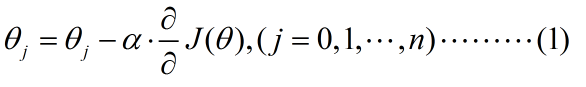
可以看到，这是一个θ值不断迭代的过程，其中α是学习速率，就是θ的移动“步幅”，后面的偏导数数就是梯度，可以理解为cost函数在θ当前位置，对于j位置特征的下降速度。
对于二维空间，梯度可以理解为函数图像的切线斜率。即：特征是一维的
对于多维特征，cost函数的图像就应该是这样的，下面举个例子：
图1 cost函数举例
这是一个二维特征的cost函数的图像，这个时候，梯度有无限多个，我们不能只说cost函数的梯度，应该说，cost函数在某个方向上的梯度。例如，cost函数在θ0方向上，在(θ0=m,θ1=n)上的梯度就是cost函数与θ1=n这个平面的交线在（m,n）处的斜率。
上面的描述比较抽象，简单说来，假设图像就是一个小山坡（有点像吧），你站在图像的（m,n）点处，朝θ0的方向看过去，看到的“山坡”的“坡度”就是上面所说的梯度了。
这个迭代过程，用形象化的语言描述，就是：
我站在山坡上，找到一个初始点θj,每次我沿着某一个方向走α这么长的路，由于总是朝着梯度的方向走，我总会走到山坡底（也就是cost函数的极小值）。
然而，这样的“盆地”可能有多个，我们不同的走法，可能会走到不同的山底，如图：
图2 多“山谷”cost函数
这里的两条路线分别走向不同的山谷，这就说明：梯度下降算法只能求出一个局部最小值，不一定是全局最小值，但这不影响它是一个好的方法。
这样，θ的迭代过程就讲清楚了。接下来说一下迭代的终止条件。
迭代肯定不是无限下去的，我们不妨想一下：当我们走到了山谷，再想往某个方向走的时候，发现都不能再往下走了，那么我们的旅行就终止了。
同样，当θ迭代了n次后（就如图2的黑线一样），发现接下来走α这么长的路，下降的高度很小很小（临界值），或者不再下降，甚至反而往上走了，所以我们的迭代终止条件就是cost函数的减少值小于某个值。
我们再来回顾一下迭代公式（1）：其中α是经验设定，称之为learning rate，初始值也是随机选定，那么后面的那个梯度呢？
梯度就是cost函数对于特征向量某一维的偏导数。我们来看看这个怎么推导和简化。
【梯度的求解】
先来写一下大致的推导过程：
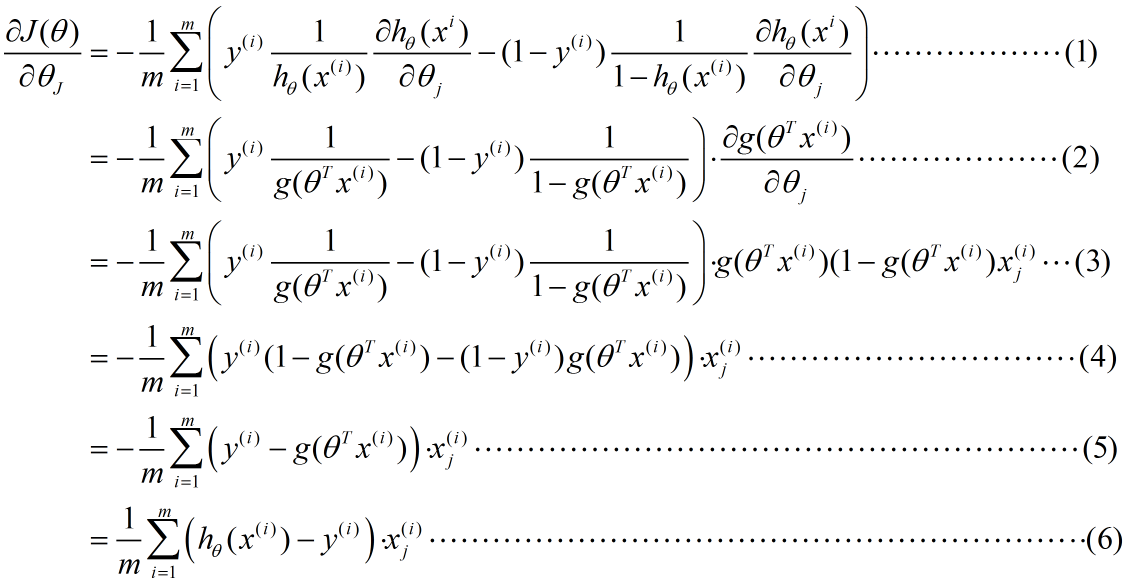
稍微解释一下推导流程，便于理解。
(1)--->(2)：使用sigmoid函数的形式g(z)替换hθ(x)、提出公因子，放在式子尾
(2)--->(3)：这一步具体推导如下（使用了复合函数的求导公式）
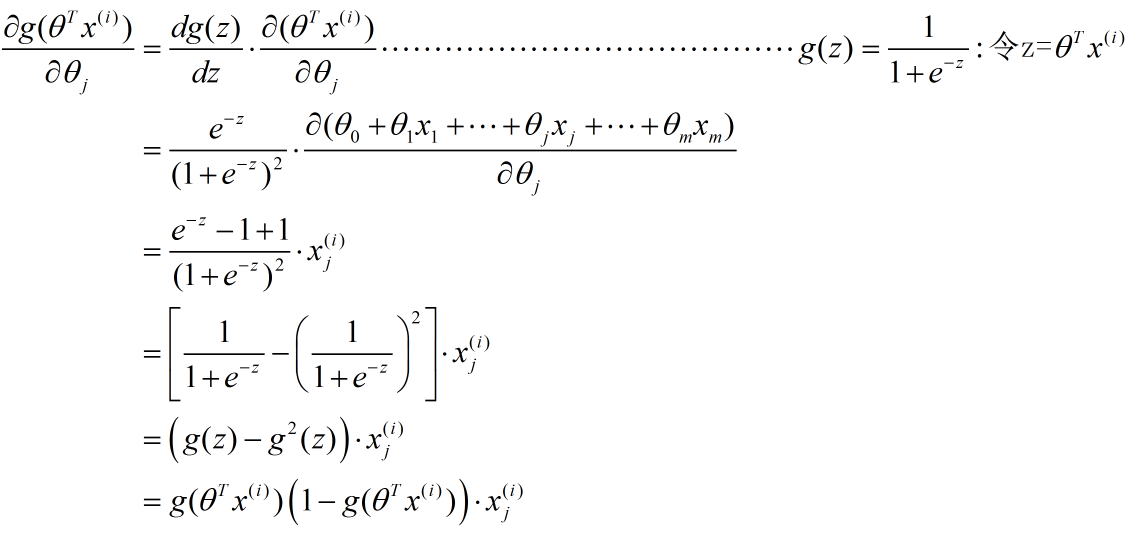
后面的几步较为简单，就不另作说明了。
【算法运行】
到了这里，我们推出了迭代公式的最终形式：
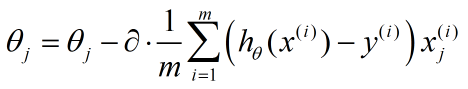
更一般的形式就是把j去掉，表示对特征的每一维都如此迭代
注意，在迭代过程中，θ的所有特征是同步更新的，所以根据给定的数据集，就能使用梯度下降算法来求解θ了，迭代终止条件即是将当前θ带入cost函数，求出代价值，与上一个代价值相减，结果小于阈值，立即停止迭代。
结语
公式推导用的也就是偏导数的求解等少量数学公式，关键是体会局部最优的思想
