索引 堆
为什么引入索引堆
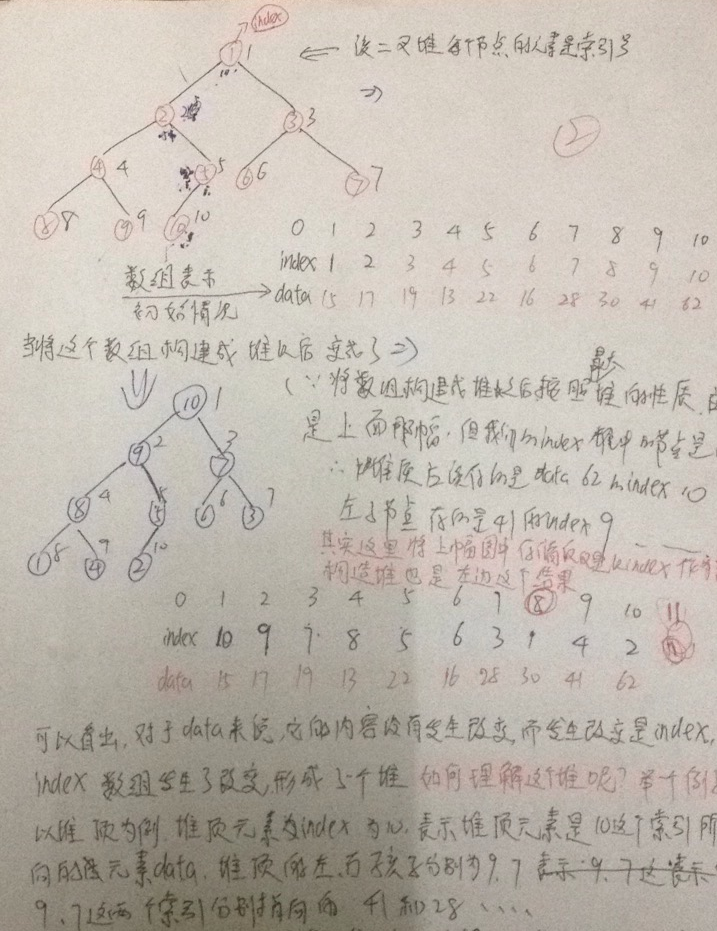
首先给定一个数组,通过heapify过程,将该数组构造成一个最大堆,
构建前和构建后,我们关注的数组,数组元素位置发生了改变,正式由于改变, 才可以仍然将数组看成堆,但是,我们这里是以整数为例的,改变过程无论是交换还是赋值操作都相对简单,但如果元素类型是字符串这样相对复杂的结构呢?那么交换操作花费的时间相对比较大,这种性能消耗还是可以解决的,另一个问题是整个元素在堆中的位置发生了改变,使得堆建成以后很难索引到,索引不到,就无法改变。举个系统任务优先级的例子,假设数组中元素索引号为1的系统任务的优先级是15,索引为2的系统任务的优先级是17....把这个数组数组构建成堆以后,索引和优先级之间的对应关系发生了改变,如果再想改变原来某个索引对应的任务的优先级,因为没有对应关系,而发生的改变也没有规律可循,就没办法实现目标了,所以,可以在堆这个类中引入一个index属性,保存原来data的索引号,并且将索引构建成堆
两种构建堆的方式对比
data属性构建堆
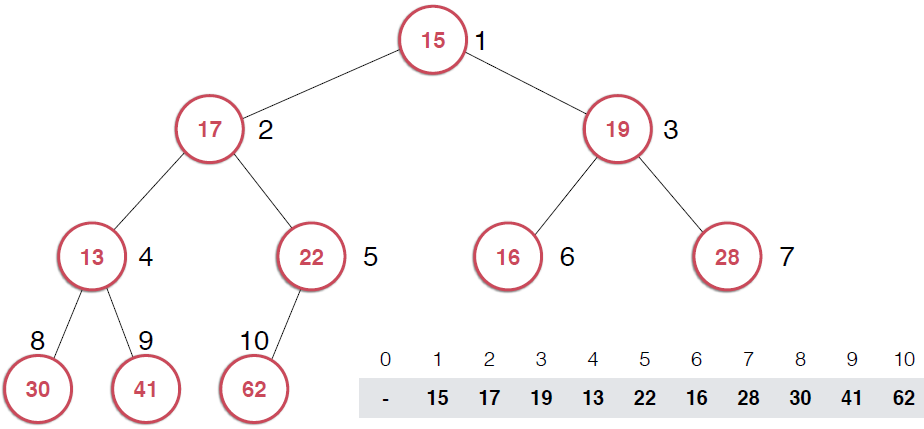
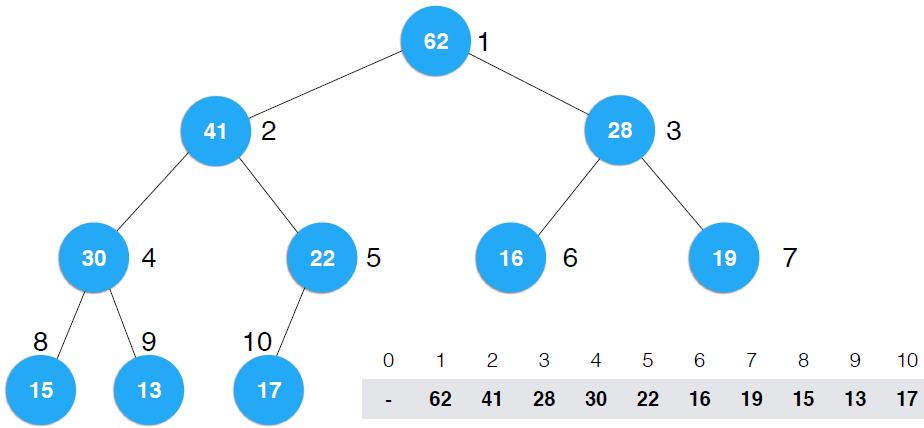
构建前 构建后
图(1)
index属性构建堆

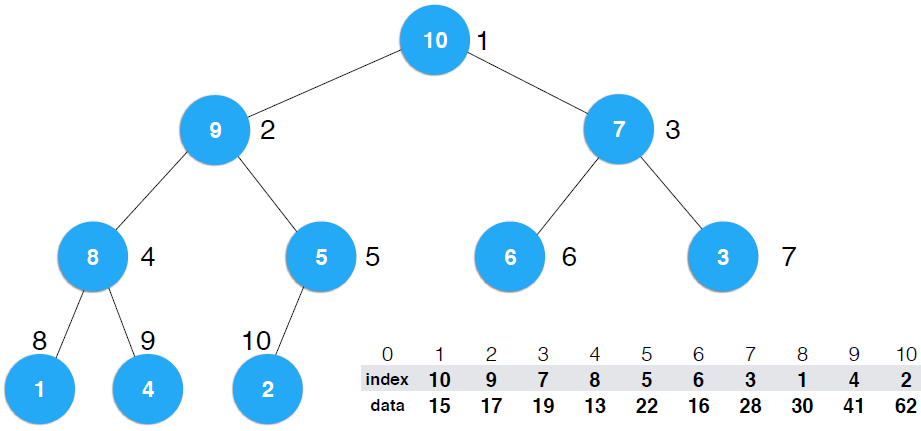
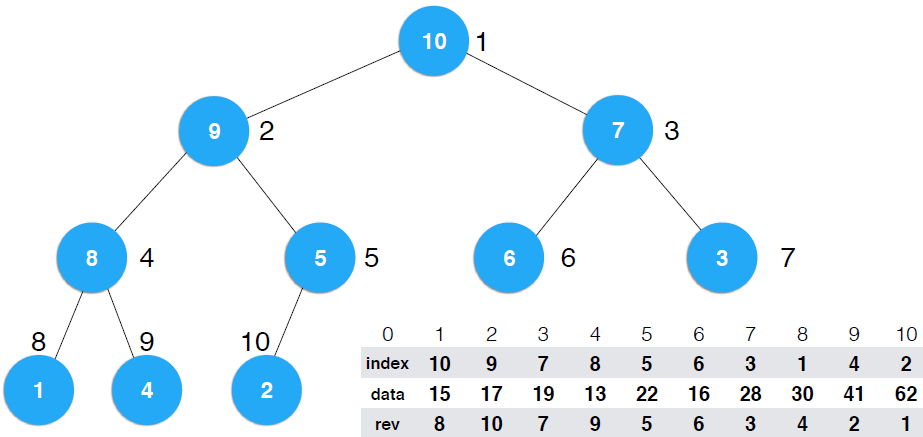
构建前 构建后
图(2)
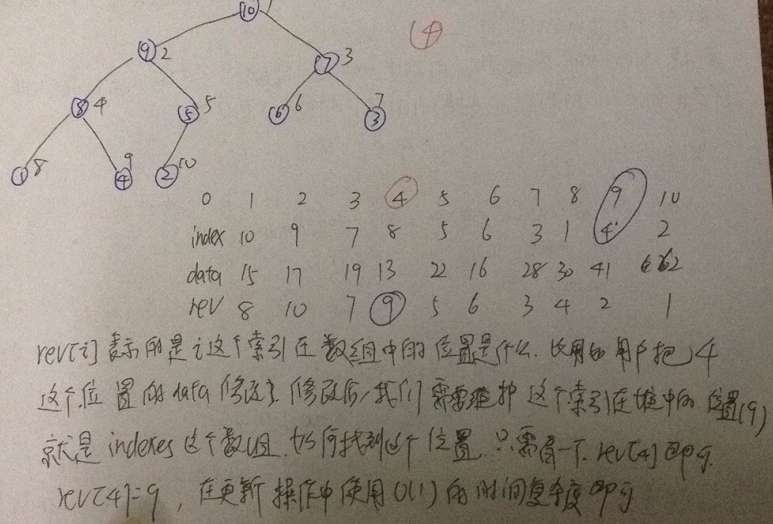
这里,我在纸上手动构建了一遍,直接从index构建堆,就是图(2)中的左图,一步步构建成最大堆,显然结果是右图,同时,图(1)中的data构建堆后,图(1)的右图和图(2)的右图是对应的。但是,在index heap中,构建堆后,data位置并没有发生改变,发生改变的是index,还是举个例子方便理解。,堆顶元素的index为10,表示堆顶元素是10这个索引所指向的元素data:62,它的左右子节点分别是9和7,9和7这两个索引分别指向41和28......
这种构建堆堆的方式的优点:
1.构建堆的过程只是索引发生变化,交换,索引是int型,操作相对简单
2.如果想对堆中数据进行操作,比如想改变进程号为7的任务的的优先级(这里是28)改变成20,那么改变后,就需要重新维护队的性质,这时只需要根据新的data来改变index,这就是index_heap
创建index heap
创建index heap的思路和创建heap的思路是一样的,只是,元素比较的时候是比较的data,但是交换的是index
完整代码:

1 template<typename Item> 2 class IndexMaxHeap{ 3 private: 4 Item* data; 5 int* indexes; 6 int count; 7 int capacity; 8 private: 9 void shiftUp(int k){ 10 while(k>1){ 11 if(data[indexes[k/2]]<data[indexes[k]]){ 12 swap(indexes[k/2],indexes[k]); 13 k/=2; 14 } 15 } 16 } 17 18 void shiftDown(int k){ 19 shilw(2*k<=count){ 20 int j = 2*k; 21 if(data[indexes[j]]<data[indexes[j+1]]) 22 j+=1; 23 if(data[indexes[k]]<data[indexes[j]]){ 24 swap(indexes[k],indexes[j]); 25 k=j; 26 } 27 } 28 } 29 public: 30 IndexMaxHeap(int capacity){ 31 data = new Item[capacity+1]; 32 indexes = new int[capacity]; 33 this->capacity = capacity; 34 count =0; 35 } 36 ~IndexMaxHeap(){ 37 delete[] data; 38 delete[] indexes; 39 } 40 int size(){return count;} 41 bool isEmpty(){return count==0;} 42 43 void insert(int i,Item item){ 44 assert(count+1<=capacity); 45 assert(i+1>0 && i+1<=capacity); 46 i+=1; 47 count+=1; 48 data[i] = item; 49 indexes[count]=i; 50 shiftUp(count); 51 } 52 53 Item extractMax(){ 54 assert(count>0); 55 Item item = data[indexes[1]]; 56 swap(indexes[1],indexes[count]); 57 count--; 58 shiftDown(1); 59 return item; 60 } 61 62 int extractMaxIndex(){ 63 assert(count>0); 64 int idx = indexes[1]; 65 swap(indexes[1],indexes[count]); 66 count--; 67 shiftDown(1); 68 return idx; 69 } 70 71 Item getMax(){return data[indexes[1]];} 72 int getMaxIndex(){ 73 assert(count>0); 74 return indexes[1]-1; 75 } 76 // get the data value whose index is i 77 Item getItem(int i){ 78 assert(i+1>0 && i+1<=capacity); 79 return data[i+1]; 80 } 81 // assign a new value for the data whose index is i 82 void change(int i,Item item){ 83 i+=1; 84 data[i] = item; 85 for(int j= 1;j<=count;j++) 86 if(indexes[j]==i){ 87 shiftDown(j); 88 shiftUp(j); 89 } 90 } 91 };
优化
前面的index heap 虽然解决了改变堆中元素,由于data位置是不改变的,所以可以通过 data[i] = newItem; 但是,改变index数组以维护队的性质这个操作就无法通过一步实现了,此时,需要先遍历indexes数组,时间复杂度是O(N),再调整的时间复杂度是O(logN),所以T(N) = O(N0+O(logN),比如,我们想要改变所以位置4的data,更改后要维护这个堆,这个堆中存储的元素是上一行的索引,所以要在indexes数组中找到4所在位置,需要遍历indexes数组,找到是第9个位置,然后对滴9个位置调整,如果,我们在对这个类中添加一个reverse属性,关系如下:


1 template<typename Item> 2 class IndexMaxHeapO{ 3 private: 4 Item* data; 5 int* indexes; 6 int* reverse; 7 int count; 8 int capacity; 9 private: 10 void shiftUp(int k){ 11 while(k>1){ 12 if(data[indexes[k/2]]<data[indexes[k]]){ 13 swap(indexes[k/2],indexes[k]); 14 reverse[indexes[k]]= k; 15 reverse[indexes[k/2]] = k/2; 16 k/=2; 17 } 18 } 19 } 20 21 void shiftDown(int k){ 22 while(2*k<=capacity){ 23 int j = 2*k; 24 if(data[indexes[j]]<data[indexes[j+1]]) 25 j+=1; 26 if(data[indexes[k]]<data[indexes[j]]){ 27 swap(indexes[j],indexes[k]); 28 reverse[[indexes[k]]] = k; 29 reverse[indexesj]=j; 30 k=j; 31 } 32 } 33 } 34 public: 35 IndexMaxHeapO(int capacity){ 36 data = new Item[capacity+1]; 37 indexes = new int[capacity+1]; 38 reverse = new inr[capacity+1]; 39 //initialize reverse[i]=0:index i does not exsit in heap 40 for(int i =0;i<=capacity;i++) 41 reverse[i] =0; // initialize reverse befor 42 this->capacity = capacity;// initialize the capacity 43 count = 0; // and count 44 } 45 ~IndexMaxHeapO(){ 46 delete[] data; 47 delete[] indexes; 48 delete[] reverse; 49 } 50 51 int size(){return count;} 52 bool isEmpty(){return count==0;} 53 54 void insert(int i,Item item){ 55 assert(count+1<=capacity); 56 assert(i+1<=capacity && i+1>0); 57 assert(!contain(i)); 58 i+=1; 59 data[i] = item; 60 indexes[count+1] =i; 61 reverse[i] = count+1; 62 count++; 63 shiftUp(count); 64 } 65 bool contain(int i){ 66 assert(i+1<=capacity && i+1>0); 67 return reverse[i+1]!=0; 68 } 69 70 Item extractMax(){ 71 Item item = data[indexes[1]]; 72 swap(indexes[1],indexes[count]); 73 reverse[indexes[count]]=0; 74 count--; 75 if(count){ 76 reverse[indexes[1]]=1; 77 shiftDown(1); 78 } 79 return item; 80 } 81 82 int extractMax(){ 83 int idx = indexes[1]-1; 84 swap(indexes[1],indexes[count]); 85 reverse[indexes[count]]=0; 86 count--; 87 if(count){ 88 reverse[indexes[1]]=1; 89 shiftDown(1); 90 } 91 return idx; 92 } 93 Item getMax(){ 94 assert(count>0); 95 return data[indexes[1]]; 96 } 97 Item getItem(int i){ 98 assert(contain(i)); 99 return data[i+1]; 100 } 101 102 void change(int i,Item newItem){ 103 assert(contain(i)); 104 i+=1; 105 data[i] = newItem; 106 shiftDown(reverse[i]); 107 shiftUp(reverse[i]); 108 } 109 };
总结
对于堆这种数据结构,尤其是index heap和i加入reverse 属性的index heap,如果直观上不好分析,可以在纸上画画,手动实现一遍操作过程,也可以像我那样将分析过程写下来,写的过程有助于分析