堆和堆排序

堆和优先队列

普通队列：FIFO，LILO

优先队列：出队顺序和入队顺序无关，和优先级相关。一个典型应用就是操作系统中。动态选择优先级高的任务执行

堆的实现

最典型的堆就是二叉堆，就像是一颗二叉树。这个堆的特点，下图可以看出：

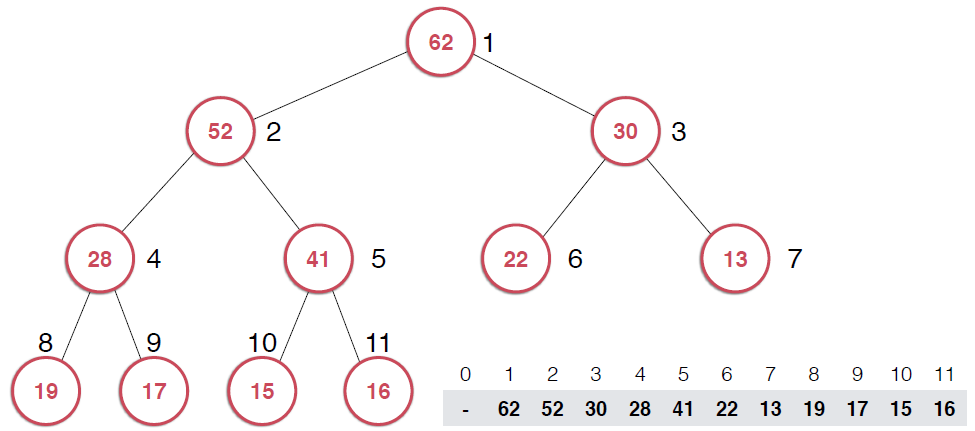
这里以最大堆为例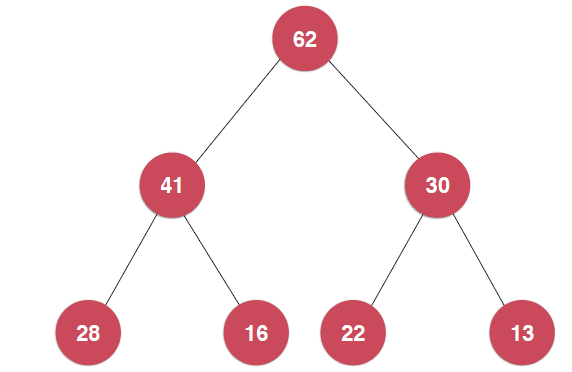，，每一个节点都不大于其父亲节点。另外，堆必须是一颗完全二叉树，正因为此，我们可以使用数组来存储二叉堆如下图所示，给二叉堆自上而下，自左到右表上序号，

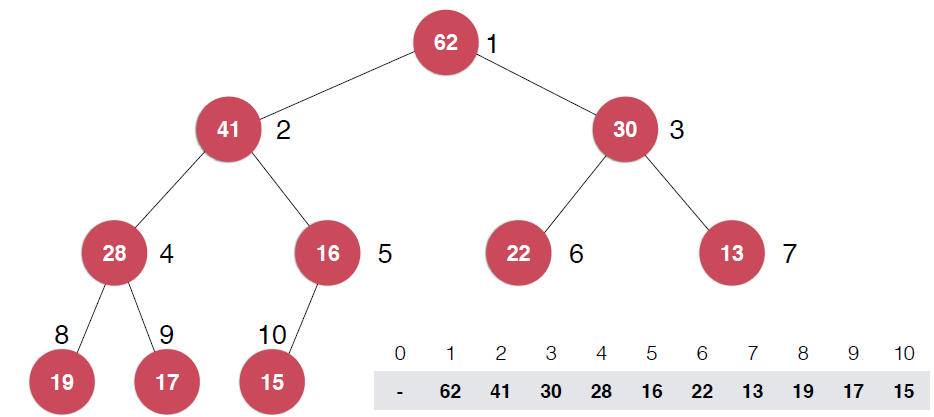
由图中节点序号，可以看出，如果某个节点的序号为k,则其左子节点的序号是2*k,右子节点的序号是2*k+1,这里，与通常我们数组的规定不同，根节点是从1开始的，不是0，这也是堆的经典实现方式。不过从0开始标定，也会有类似性质，只是常数的变化。

下面就要实现最大堆，做成一个MaxHeap 类，最大堆中要存储数据，为了通用性，将这个类做成一个模板类。这个最大堆首先得有一个存储数据的数组，在用户定义之前，我们不知道数组的大小，所以该数组是一个指针类型，相应的会在构造函数中初始化该数组。还需要一个int型的size来表示堆中元素数量。所以堆的基本框架如下：

template<typename Item>
class MaxHeap{
private:
    Item* data;
    int count;
private:
    int shiftDown(int k){

    }
public:
    MaxHeap(int capacity){
        data = new Item[capacity];
        count=0;
    }
    ~MaxHeap(){
        delete[] data;
    }

    int size(){return count;}

    bool isEmpty(){return count==0;}
};

 向堆中添加、删除元素

添加元素

因为堆的性质，我们这里要用到一个添加元素时的核心操作。、；shiftUp，用下面的堆具体说一下思路

    

 

 

 

  

 

  

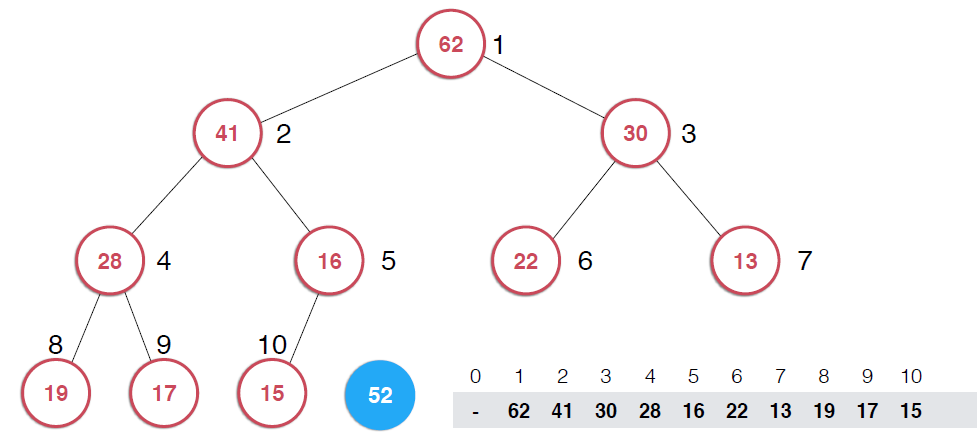
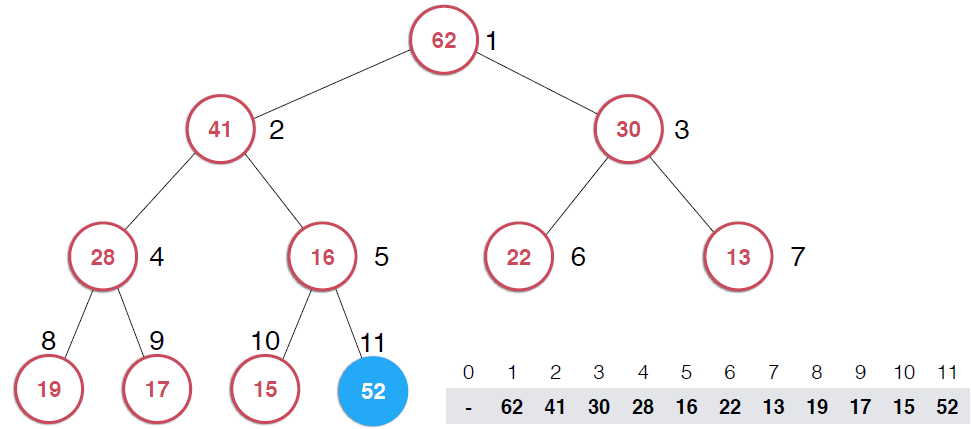
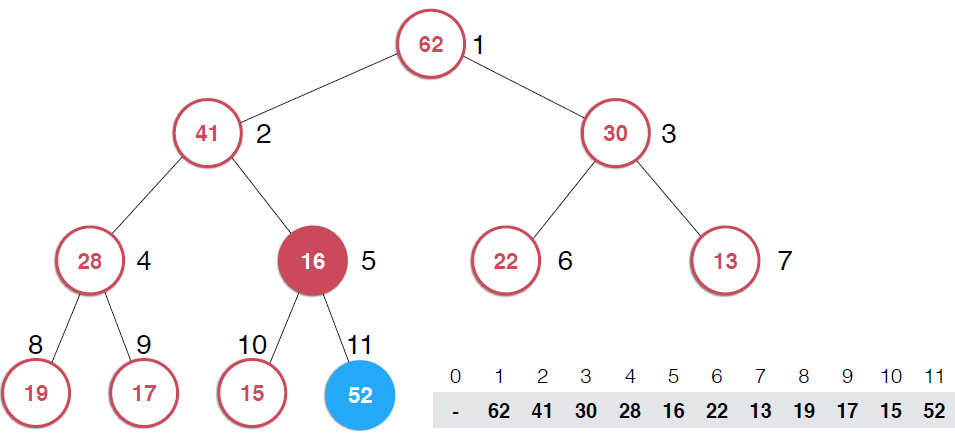
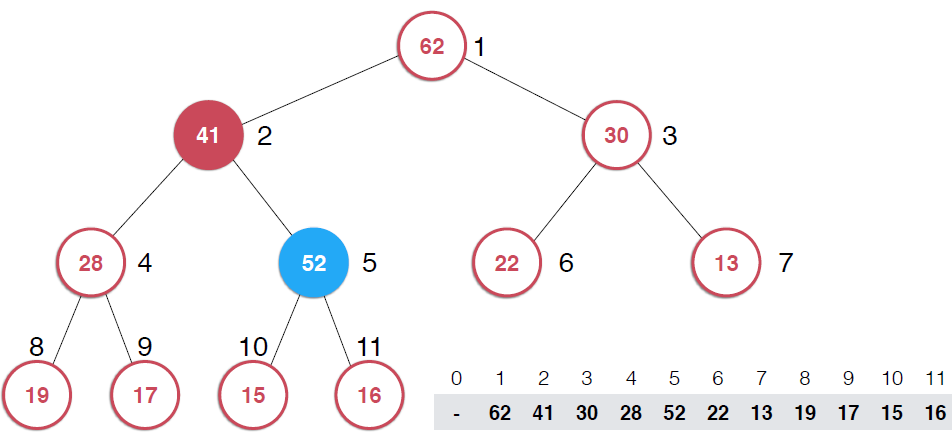
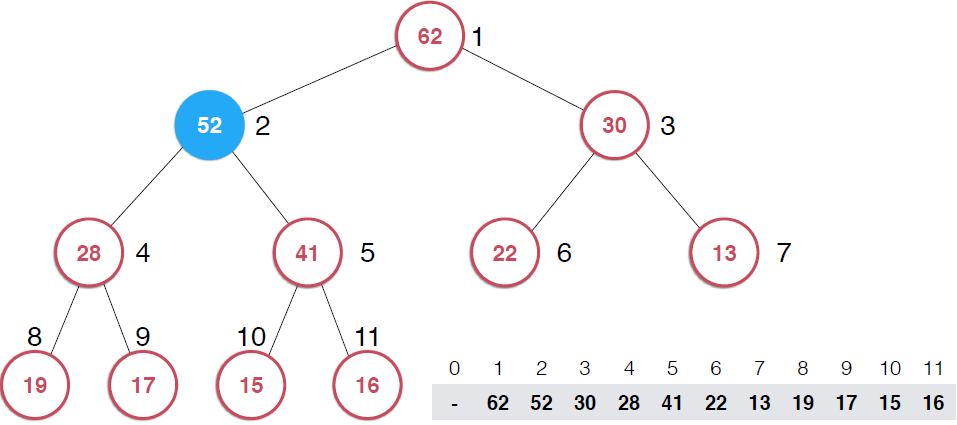
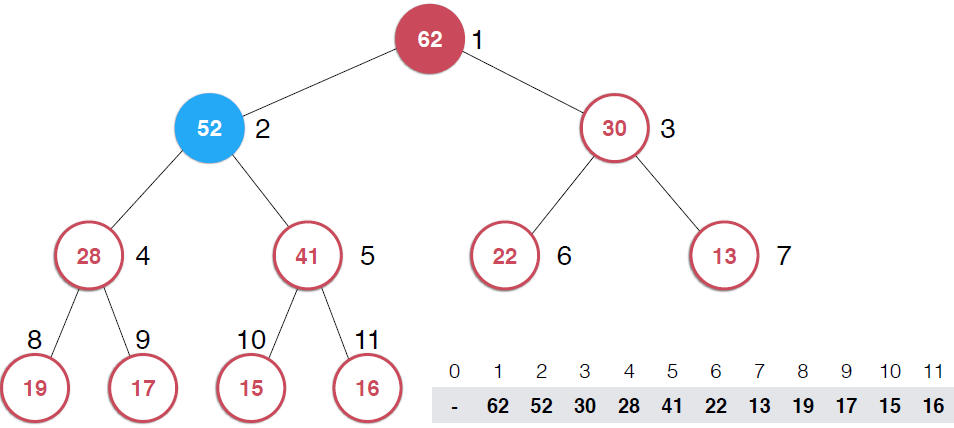
 因为是用数组存储的堆中的元素，最初52加入的时候如第二幅图所示，由于新元素的加入，这个堆已经不满足最大堆的性质了，我们需要根据最大堆的性质调整，给52找到正确的位置，如何调整呢？：考查52的父节点，比52小，违背了最大堆的性质，所以交换之，这样以52为根节点的子堆满足了最大堆的性质，继续考查新的堆中52的父节点，依然不满足最大堆的定义，同样的操作，继续考查，直到整个堆满足最大堆的性质。那么添加元素后只需要不断调用shiftUp操作就可以了，具体代码实现

// insert(Item)
 2 void insert(Item item){
 3         data[count+1] =item;
 4         count++;
 5         shiftUp(count);
 6     }
 7 
 8 // shiftUp(int)
 9 
10 void shiftDown(int k){
11         while(data[k/2]<data[k] && k>1){
12             swap(data[k],data[k/2]);
13             k/=2;
14         }
15     }

但是， data[count+1] =item; 有一个数组越界的潜在风险，所以，我们需要在类中再定义一个capacity的成员变量，并在构造函数中使用用户指定的capacity初始化 this->capacity = capacity; 并且，在添加新元素之前assert一下，在insert(Item)函数中第三行之前加入 assert(count+1<=capacity); 当然，更好的方法就是一旦发现capacity不足够，就分配新的空间，C++primer中在讲容器的时候提到过，一般是采用倍增的方法，这里主要讲堆，我自己也没研究过，这里先Mark下，以后仔细想想具体实现，此处就先用这种简单的方法防止数组越界。

从堆中取出元素

Note： 从堆中取出元素只能取出根节点的元素。

一旦取出对顶元素，就需要调整堆，使得堆这颗二叉树依然满足堆的性质。还是以图的形式给出过程。

 

 

  

 

  

 

  

 

 

 

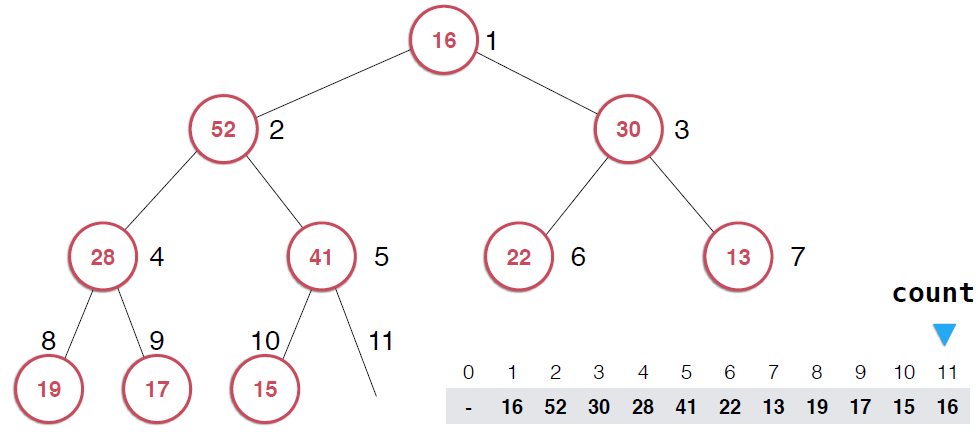
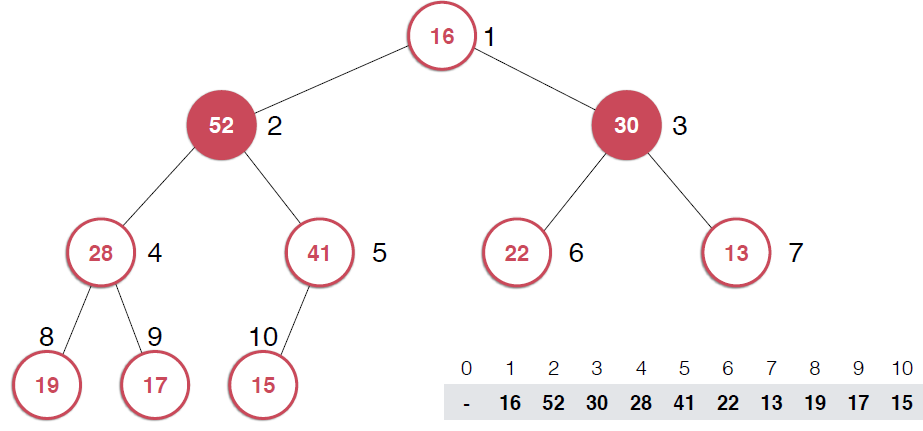
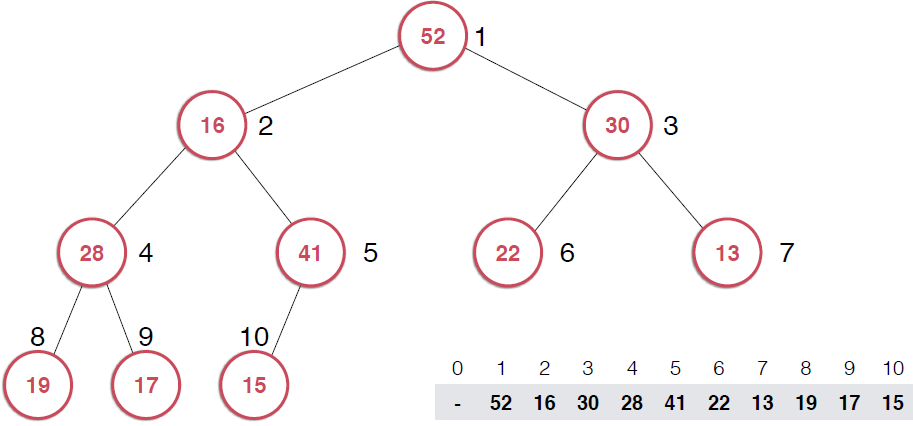
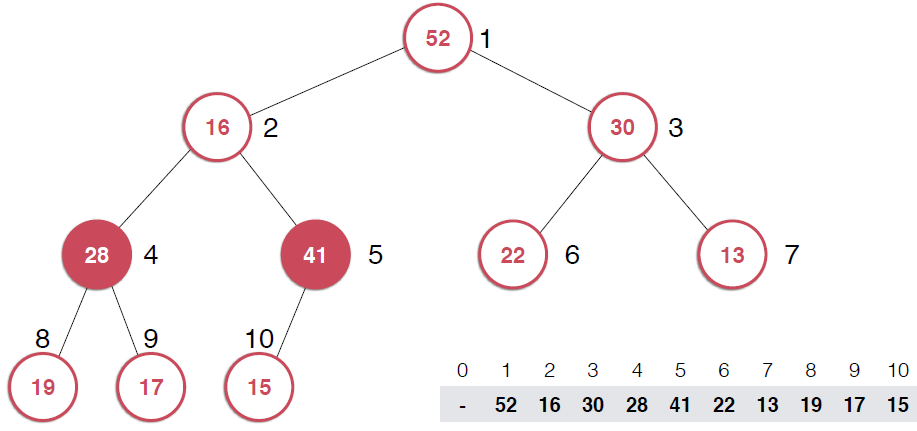
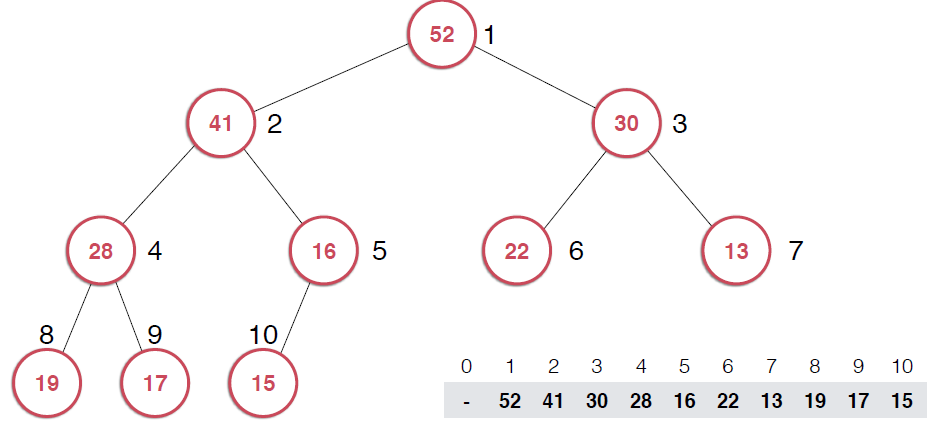
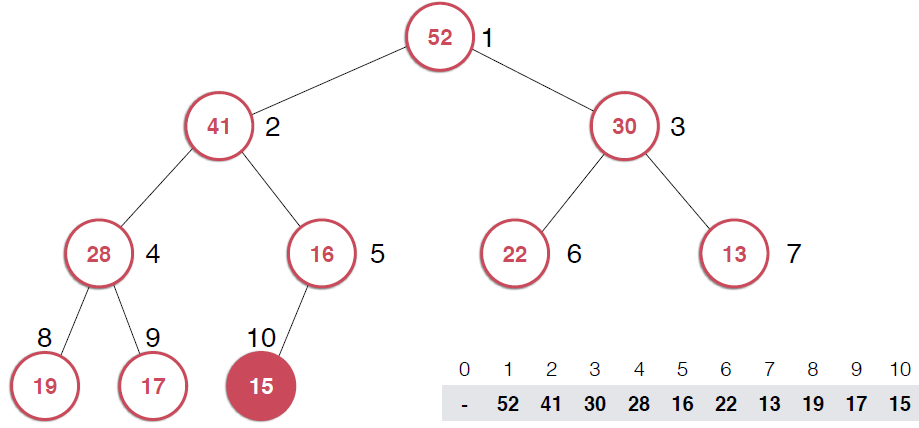
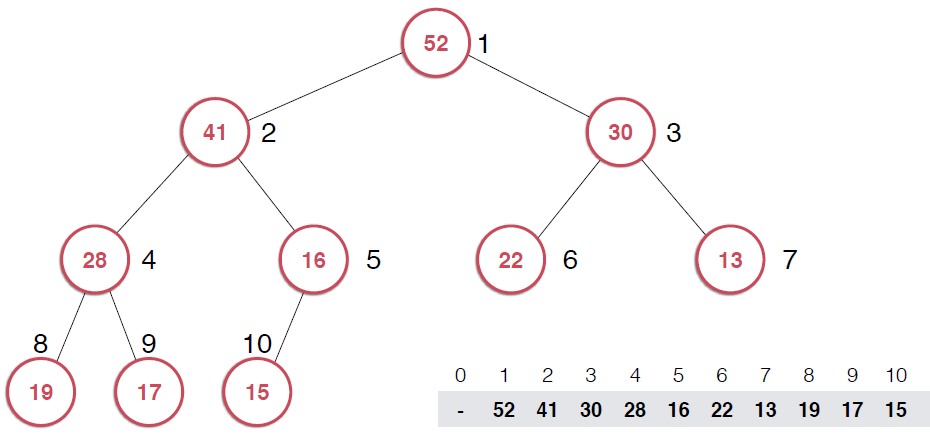
 由上面过程可以看出，一旦取出堆顶元素，就把堆中最后一个元素放到堆顶，不断调整，直到这颗二叉树再次满足最大堆的性质。这个不断调整的过程就是shiftDown 的过程。简单说一下这个过程。现在16处在堆顶位置，比它的左右子节点都要小，最大堆的性质要求父亲节点要大于子节点，所以，应该调整，向左还是向右是有左右的大小决定的，谁大跟谁换，这样16跟52换，然后再考查新的堆，继续考查16，直到16在它正确的位置。具体实现如下：

//shiftDown(int);
void shiftDown(int k){
        //int j = 2*k;
        while(2*k<=count){
            int j = 2*k;
            if(data[j]<data[j+1])
                j++;
            if(data[k]<data[j]){
                swap(data[k],data[j]);
                k = j;
            }
        }
    }

//get the top of heap Item top()
Item get(){
        assert(count>0);
        Item item  = data[1];
        swap(data[1],data[count])
        count--;
        //swap(data[])
        shiftDown(1);
        return item;
    }

前面给出了取出对顶元素的方法，如果，不断取出堆顶元素并打印出来，就是一个从大到小的数组，由此，可以想到利用堆进行排序，这个排序接收一个数组和数组元素个数，创建一个heap类的对象，通过这个对象调用insert()函数和top() 函数即可实现，具体实现

void heap_sort(int arr[],int n){
    MaxHeap<int> maxHeap = MaxHeap(n);
    for(int i = 0;i<n;i++)
        maxHeap.insert(arr[i]);
    for(int i = 0;i<n;i++)
        arr[i] = maxHeap.top();
}

上面实现的是从大到小的排序，要想从小到大排序，反向打印就可以，只需将第5行改为 for(int i = n-1;i>=0;i--) 

堆的heapify

前面提到了最大堆排序，我将上面的堆排序实现方式与归并排序和快速排序时间做了一个比较，前面的堆排序的方式花费的时间较长，回顾一下，前面的堆排序需要将数组元素一个一个的插入堆中，利用堆不断的调整，从堆中取出元素的时候也需要不断的调整，使得二叉树依然保有最大堆的性质，这种方式的效率显然不高，说道这里，我想起来了，不断调整过程中需要不断的shiftUp和shiftDown，这两个操作都需要swap()操作，前面讲插入排序的时候提到过，swap操作相对于移动/赋值操作是低效的，所以，这里也是可以改进的，不过下面要说的是改进数组构成堆的方式，给定一个数组，我们让这个数组形成一个堆的形状，这个过程叫--Heapify.还是以图片形式演示过程，下图只给出了一部分过程的图示

 

 

 

 

 

  

 

 

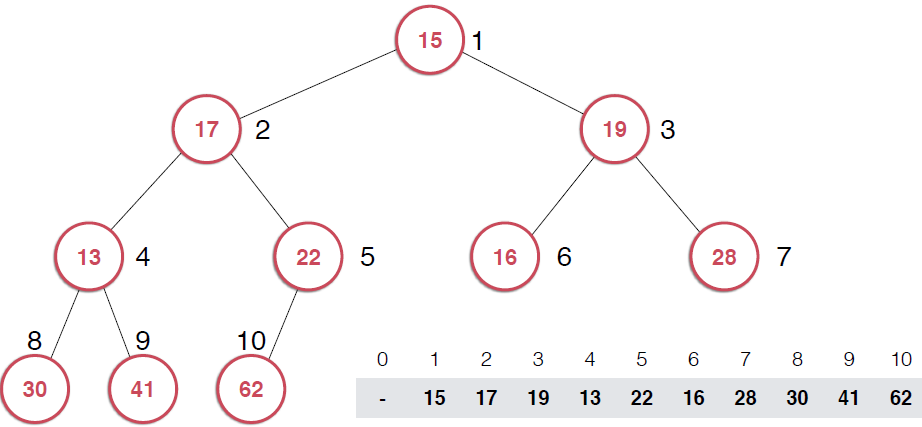
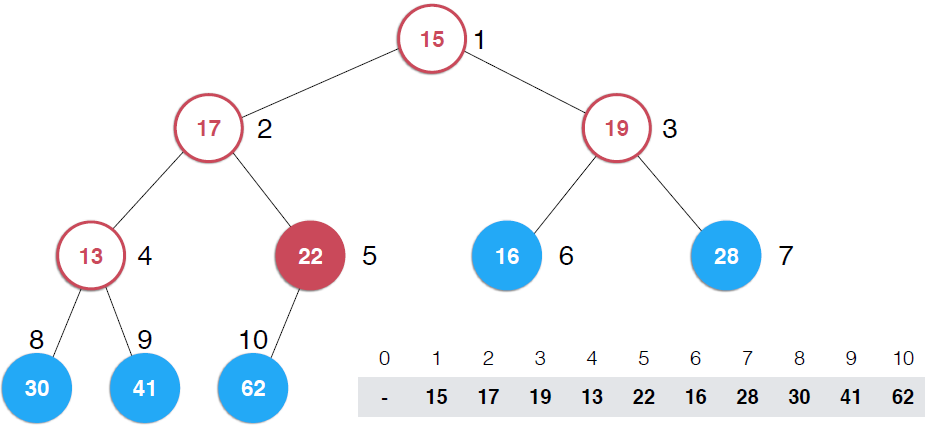
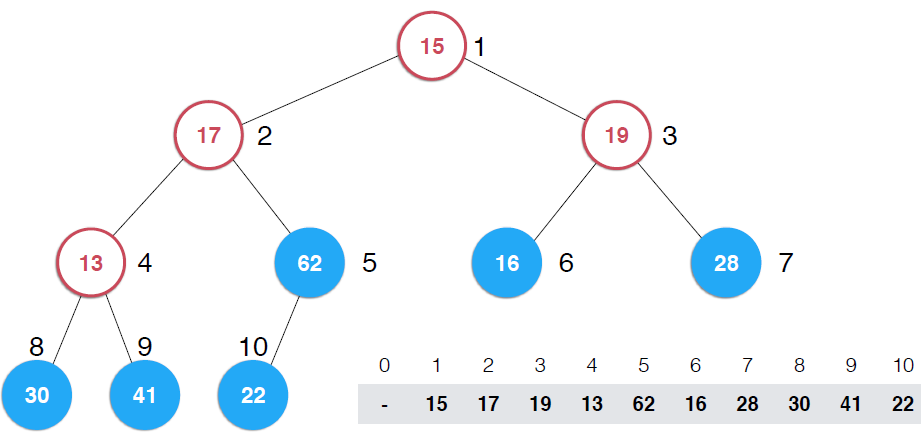
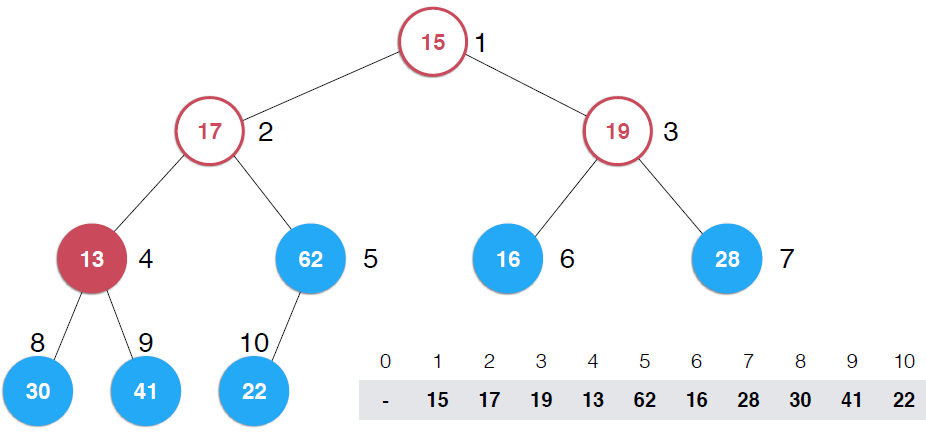
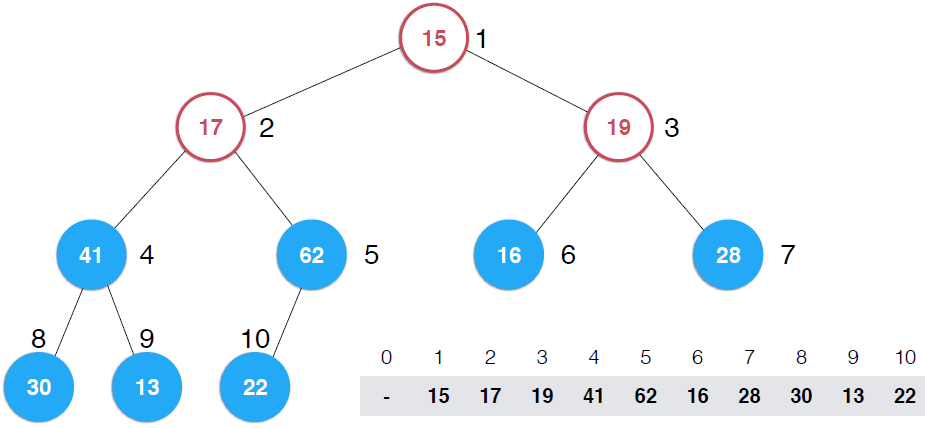
 看第一幅图，右下角是一个数组，将该数组构建成一颗完全二叉树，但是，这颗二叉树不是堆，如果将这颗完全二叉树根据对的性质调整成堆，那么，就将数组构造成了堆，调整过程就是上图示过程

看第二幅图中所有叶子节点，它们本身各自就是一个堆，还是以最大堆为例，一个最大堆，Note：一颗完全二叉树，第一个非叶子节点是5，元素数目为10，可以多举些例子，可以找出规律，一颗完全二叉树第一个非叶子节点是k/2取整（k为完全二叉树节点个数），这里是上取整，并且是从1开始而不是从0开始（可以证明的）。现在自下而上考查非叶子节点，第一个是5，它的值是32，以它为根的子树不满足最大堆的性质，它比子节点小，所以做一次shiftDown操作，接着考查4位置，13也比子节点小，再执行一次shiftDown操作，接着考查位置3，也不满足，继续执行shiftDown，再看2 ，17比它的子节点小，shiftDown，但是调整到5上，依然不满足，继续shiftDown，直到17在正确的位置上， 这时，以62为根的子树满足了最大堆性质，接着向上一层，树顶元素不满足，shiftDown，直到调整到15应该在的位置。可以构建一个构造函数接收一个数组和数组容量，代码实现如下

MaxHeap(Item arr[],int n){
        data = new Item[n];
        capacity = n;
        for(int i =0;i<n;i++)
            data[i+1] = arr[i];
        count = n;
        for(int k = n/2;k>0;k--)
            shiftDown(k);
    }

使用这个构造函数进行heapsort

void heap_sort2(int arr[],int n){
    MaxHeap<int> maxHeap = MaxHeap(arr,n);
    for(int i = n-1;i>=0;i--)
        arr[i] = maxHeap.top();
}

再次测试，时间性能上比前面的堆排序快，但依然是比归并排序和快速排序慢，不过堆排序通常用于动态数据的维护，而不是系统级别的排序。

将n个元素逐个插入到一个空堆中，时间复杂度是O(NlogN)的

但是heapify的过程，算法复杂度是O(N)，这个，我没有证明。只是看书上写的

原地堆排序

前面介绍的堆排序算法都需要将数据从数组放入堆中，再从堆中取出。这需要分配额外的空间，但是，根据堆排序的思想，整个数组的排序过程可以原地进行，不需要再分配额外空间。回想之前通过数组构造堆的过程可以看出一个数组其实可以把它看成一个堆，因此可以将数组通过heapify过程构建成堆，还是以最大堆为例。 这是一个数组形式排列的最大堆，堆顶元素v为整个数组中最大的，按照排序后的结果，v应该在数组尾部，所以将v与最后一个元素w交换，交换后这个数组不再是一个最大堆（橙色部分不再是最大堆），如何调整成最大堆，根据前面的，就是不断的调用shiftDown，调整成一个最大堆（依然用暗红色表示该部分是最大堆），蓝色表示已经排序好的。

 

 

 

   

  此时又重复上面的过程，继续交换v和w，然后将未排序的部分调整成最大堆。

Note：由于整个过程在数组上原地进行，数组是从0开始索引的，所以在实现的时候注意调整，主要是shiftDown过程的索引，具体的就是父亲节点与子节点索引的关系，举个例子很容易看出来

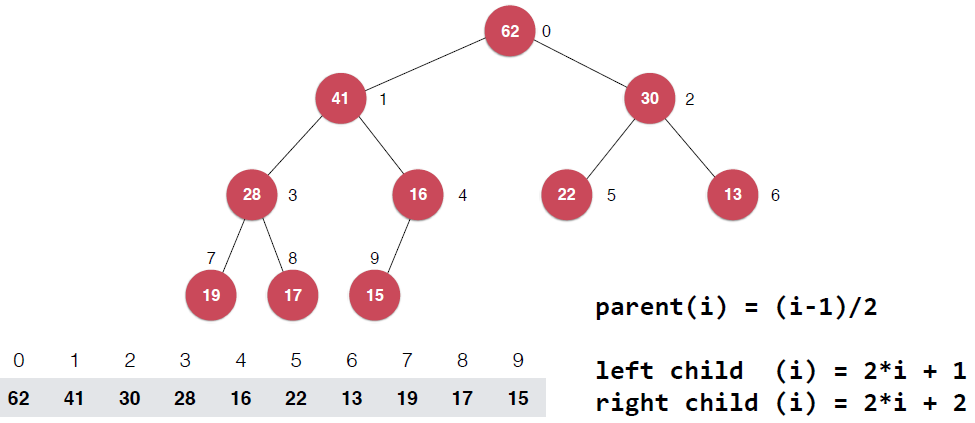
最后一个非叶子节点同时也变成了 (count-1)/2 ,依然是上取整。

实现代码如下：

 

void heapSort(int arr[],int n){
    //heapify
    // index begins with 0
    // the first leaf node which is not null (count-1)/2
    for(int i = (n-1)/2;i>=0;i--)
        __shiftDown(arr,n,i);
    for(int i = n-1;i>=0;i--){
        swap(arr[i],arr[0]);
        __shiftDown(arr,i,0);
    }
}

void __shiftDown(int arr[],int n,int k){
    while(2*k+1<n){
        int j = 2*k+1;
        if(arr[j]<arr[j+1] && j+1<n)
            j+=1;
        if(arr[k]<arr[j]){
            swap(arr[k],arr[j]);
            k = j;
        }
    }
}

优化

之前提到过，用赋值操作代替交换操作会提升时间效率，在这里实现

void __shiftDown2(int arr[],int n,int k){
    int e = arr[k];
    while(2*k+1<n){
        int j = 2*k+1;
        if(arr[j]<arr[j+1])
            j+=1;
        if(e>=arr[j]) break;
        arr[k] = arr[j];
        k = j;
    }
    arr[k] = e;
}

排序算法总结

到这里，所有排序算法都写完了，下面的图是我在GitHub上看到的关于排序算法的总结

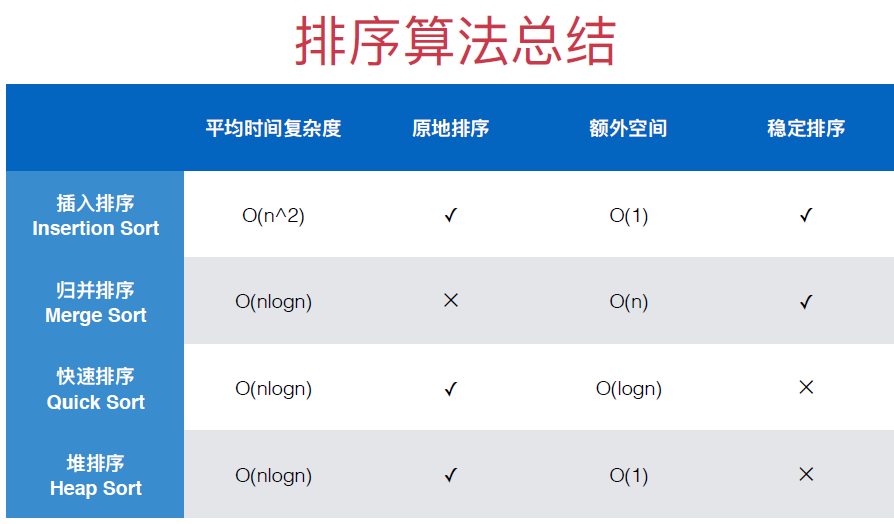
这里，有一个排序算法稳定性的概念，之前没有提到过

算法稳定性：对于相等的元素在排序后，原来靠前的元素依然靠前，相等的元素的相对位置没有发生改变

我觉得他给出的这个解释的前半句非常好理解，对于算法稳定性。