1. 布隆过滤器的概念
布隆过滤器（Bloom Filter） 是由 Howard Bloom在1970年提出的二进制向量数据结构，它具有很好的空间和时间效率，被用来检测一个元素是不是集合中的一个成员，即判定 “可能已存在和绝对不存在” 两种情况。如果检测结果为是，该元素不一定在集合中；但如果检测结果为否，该元素一定不在集合中,因此Bloom filter具有100%的召回率。
2. 布隆过滤器应用场景
- 垃圾邮件过滤
- 防止缓存击穿
- 比特币交易查询
- 爬虫的URL过滤
- IP黑名单
- 查询加速【比如基于KV结构的数据】
- 集合元素重复的判断
3. 布隆过滤器工作原理
布隆过滤器的核心是一个超大的位数组和几个哈希函数。假设位数组的长度为m,哈希函数的个数为k。
下图表示有三个hash函数，比如一个集合中有x，y，z三个元素，分别用三个hash函数映射到二进制序列的某些位上，假设我们判断w是否在集合中，同样用三个hash函数来映射，结果发现取得的结果不全为1，则表示w不在集合里面。
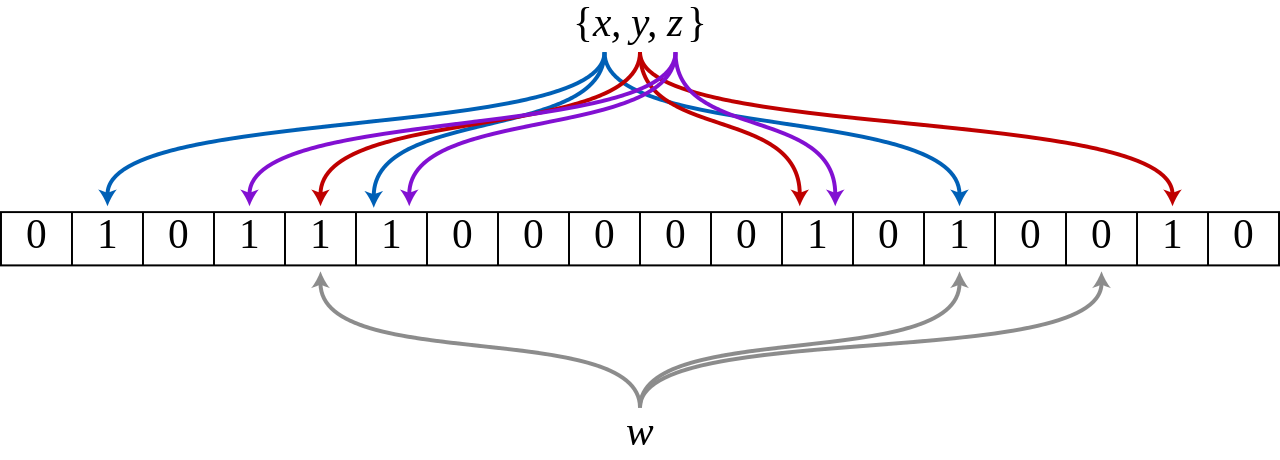
工作流程:
- 第一步：开辟空间：
开辟一个长度为m的位数组（或者称二进制向量），这个不同的语言有不同的实现方式，甚至你可以用文件来实现。 - 第二步：寻找hash函数
获取几个hash函数，前辈们已经发明了很多运行良好的hash函数，比如BKDRHash，JSHash，RSHash等等。这些hash函数我们直接获取就可以了。 - 第三步：写入数据
将所需要判断的内容经过这些hash函数计算，得到几个值，比如用3个hash函数，得到值分别是1000，2000，3000。之后设置m位数组的第1000，2000，3000位的值位二进制1。 - 第四步：判断
接下来就可以判断一个新的内容是不是在我们的集合中。判断的流程和写入的流程是一致的。
4. 布隆过滤器的优缺点
1、优点：
- 有很好的
空间和时间效率 存储空间和插入/查询时间都是常数。- Hash函数相互之间没有关系，方便由硬件并行实现。
- 不需要存储元素本身，在某些对保密要求非常严格的场合有优势。
- 布隆过滤器可以表示
全集，其它任何数据结构都不能。
2、缺点：
误判率会随元素的增加而增加不能从布隆过滤器中删除元素
5. 布隆过滤器注意事项
布隆过滤器思路比较简单，但是对于布隆过滤器的随机映射函数设计，需要计算几次，向量长度设置为多少比较合适，这个才是需要认真讨论的。
如果向量长度太短，会导致误判率直线上升。
如果向量太长，会浪费大量内存。
如果计算次数过多，会占用计算资源，且很容易很快就把过滤器填满。
6. Go实现布隆过滤器
1. 开源包简单演示
package main
import (
"fmt"
"github.com/willf/bitset"
"math/rand"
)
func main() {
Foo()
bar()
}
func Foo() {
var b bitset.BitSet // 定义一个BitSet对象
b.Set(1).Set(2).Set(3) //添加3个元素
if b.Test(2) {
fmt.Println("2已经存在")
}
fmt.Println("总数：", b.Count())
b.Clear(2)
if !b.Test(2) {
fmt.Println("2不存在")
}
fmt.Println("总数：", b.Count())
}
func bar() {
fmt.Printf("Hello from BitSet!\n")
var b bitset.BitSet
// play some Go Fish
for i := 0; i < 100; i++ {
card1 := uint(rand.Intn(52))
card2 := uint(rand.Intn(52))
b.Set(card1)
if b.Test(card2) {
fmt.Println("Go Fish!")
}
b.Clear(card1)
}
// Chaining
b.Set(10).Set(11)
for i, e := b.NextSet(0); e; i, e = b.NextSet(i + 1) {
fmt.Println("The following bit is set:", i)
}
// 交集
if b.Intersection(bitset.New(100).Set(10)).Count() == 1 {
fmt.Println("Intersection works.")
} else {
fmt.Println("Intersection doesn't work???")
}
}
2. 封装的方法：
//----------------------------------------------------------------------------
// @ Copyright (C) free license,without warranty of any kind .
// @ Author: hollson <hollson@live.com>
// @ Date: 2019-12-06
// @ Version: 1.0.0
//------------------------------------------------------------------------------
package bloomx
import "github.com/willf/bitset"
const DEFAULT_SIZE = 2<<24
var seeds = []uint{7, 11, 13, 31, 37, 61}
type BloomFilter struct {
Set *bitset.BitSet
Funcs [6]SimpleHash
}
func NewBloomFilter() *BloomFilter {
bf := new(BloomFilter)
for i:=0;i< len(bf.Funcs);i++{
bf.Funcs[i] = SimpleHash{DEFAULT_SIZE,seeds[i]}
}
bf.Set = bitset.New(DEFAULT_SIZE)
return bf
}
func (bf BloomFilter) Add(value string){
for _,f:=range(bf.Funcs){
bf.Set.Set(f.hash(value))
}
}
func (bf BloomFilter) Contains(value string) bool {
if value == "" {
return false
}
ret := true
for _,f:=range(bf.Funcs){
ret = ret && bf.Set.Test(f.hash(value))
}
return ret
}
type SimpleHash struct{
Cap uint
Seed uint
}
func (s SimpleHash) hash(value string) uint{
var result uint = 0
for i:=0;i< len(value);i++{
result = result*s.Seed+uint(value[i])
}
return (s.Cap-1)&result
}
func main() {
filter := bloomx.NewBloomFilter()
fmt.Println(filter.Funcs[1].Seed)
str1 := "hello,bloom filter!"
filter.Add(str1)
str2 := "A happy day"
filter.Add(str2)
str3 := "Greate wall"
filter.Add(str3)
fmt.Println(filter.Set.Count())
fmt.Println(filter.Contains(str1))
fmt.Println(filter.Contains(str2))
fmt.Println(filter.Contains(str3))
fmt.Println(filter.Contains("blockchain technology"))
}
100W数量级下布隆过滤器测试，源码可参考https://download.csdn.net/download/Gusand/12018239
参考：
推荐：https://www.cnblogs.com/z941030/p/9218356.html
https://www.jianshu.com/p/01309d298a0e
https://www.cnblogs.com/zengdan-develpoer/p/4425167.html
https://blog.csdn.net/liuzhijun301/article/details/83040178
https://github.com/willf/bloom
