[学习笔记] 第十课:矩阵乘法 和 高斯消元

前言

矩阵乘法在优化dp,图论算法(广义矩阵乘法优化floyd)的运算中有着广泛的应用。

预算规律

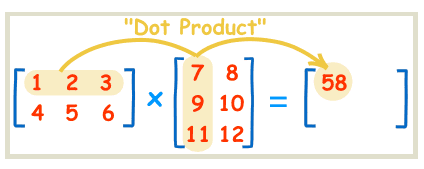
简明的来说答案矩阵的第\((x, y)\)为 A的第x行和B的第y列的乘积和。(所以这也说明了 两个矩阵要是能够相乘，那么必须满足A的行数和B的列数相同)
用代码来表示可能更为清晰

Matrix operator(const Matrix &b) const {
      Matrix c; c.init();
      for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= n; j++) {
                  for(int k = 1; k <= n; k++) {
                        c.num[i][j] = (c.num[i][j] + num[i][k] * b.num[k][j]);
                  }
            }
      }
      return c;
}

斐波那契数列

\(\text{f[i] = f[i - 1] + f[i - 2]}\)

\( \begin{bmatrix} f[1] & f[0] \end{bmatrix} \quad \)

\( \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \quad \)

矩阵具有结合律，所以直接快速幂

优化图论