[学习笔记] 基环树

知识讲解

1.定义：由\(n\)个点\(n\)条边组成的图，由一个环组成，环上每个点都是一棵树点树根，所以称为基环树。当然，一棵树上连一条边也会变成基环树。
2.一般处理方法：

	a.找到基环树上唯一的环
	b.以环上每一个点作为起点往外跑
	c.获取环上每个点的信息值
	d.转化为序列问题

例题

例题1 最短距离

题面

给定一张有\(n\) 个点\(m\) \((\)\(m = n\) 或者\(m = n - 1\)\()\) 条边的无向图，每条边有边权，而且保证这张图是联通的。现在有\(q\) 次询问，每次询问会给出两个点\(x，y，\)求\(x\) 到\(y\) 的最短路的长度。

正解

此题考察基环树概念理解
\(m = n - 1\)即位一颗树每个点对之间有且只有一条简单路径只要跑个\(lca\) 就行了
\(m = n\)此时即位一颗基环树我们可以将环上的一条边\((a, b)\)抽出来然后转化为

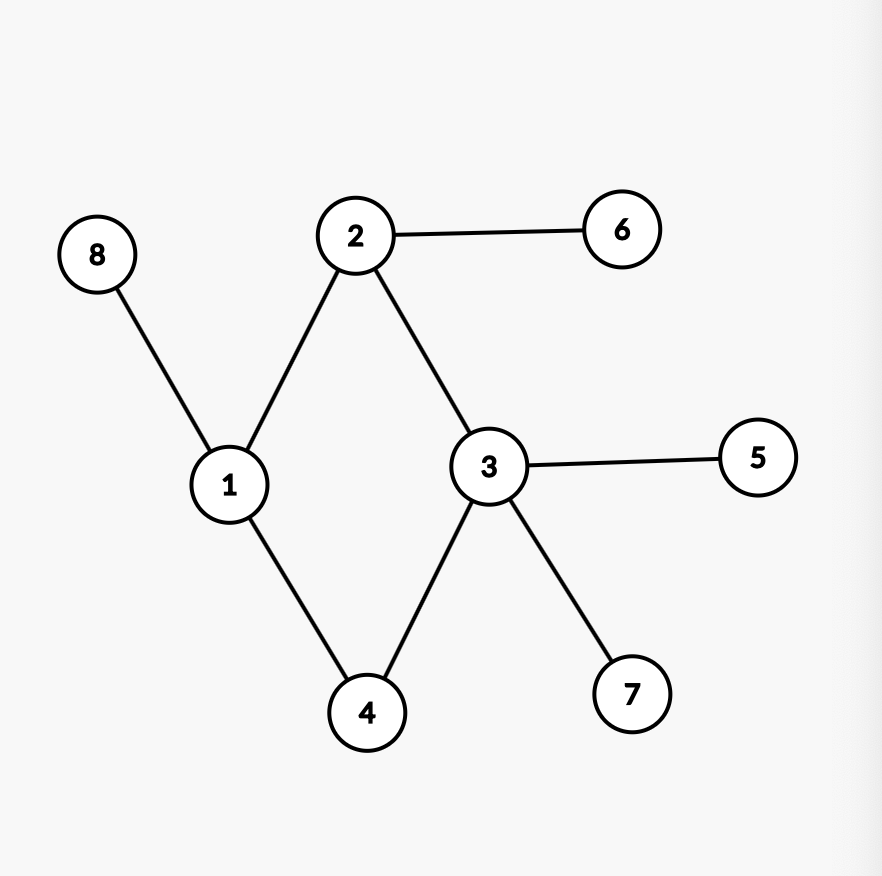
树的问题分三种情况讨论一下问题(假设被抽掉的为(2,3))

A.环外u->环外v (8->5)三种路径 
	1.树上原来的路径 path:8->1->4->3->5
	2.u->a->b->v path:8->1->2->3->5
	3.u->b->a->v path:8->1->3->2->3->5
B.环外u->环内v (8->3)三种路径 
	1.树上原来的路径 path:8->1->4->3
	2.u->a->b->v path:8->1->2->3
	3.u->b->a->v path:8->1->4->3->2->3 (显然pass)
C.环内u->环内v (1->3)两种路径 
	1.树上原来的路径 path:1->4->3
	2.连上边另外的还 path:1->2->3

综上我们可以得出任意两点间距离也可以这样得出代码也就很简单了

Code

inline void main () {
	for (int i = 1; i <= n; i ++ ) fa[i] = i;
	for (int i = 1, u, v, w; i <= m; i ++ ) {
		read (u); read (v); read (w);
		if (find (u) == find (v)) {
			last_u = u; last_v = v; last_w = w;
		} else {		
			addedge (u, v, w);
			addedge (v, u, w);
			merge (u, v);
		}
	}
	dfs (1, 0, 0);
	for (int i = 1, u, v; i <= q; i ++ ) {
		read (u); read (v);
		int ans = INF;
		chkmin (ans, min (dis (u, v), min (dis (u, last_u) + dis (last_v, v) + last_w, dis (u, last_v) + dis (last_u, v) + last_w)));
		write (ans); putchar ('\n');
	}
}

讨论一棵基环树上的最长路径的组成
\(A.\)经过环的那么答案就是环外的一点到环上在到环外的最长距离
\(B.\)不经过环的那么就是经过这个点的最长距离加上经过这个点的次长距离
\(B\)因为不进入环，所以是个简单的树形\(dp\)问题
那么我们想如何获得\(A\)的答案，首先我们定义\(f_x\)表示环上的点\(x\)向外延伸的最长距离为\(f_x\)
那么我们就要\(\max {f_x + f_y + dis (x, y)}\) \((x,y为环上的点)\)这个东西要\(O(n^2)\) 考虑如何优化
我们用式子来表示\(dis(x, y)\)
因为\(dis\)有两种走法，所以我们可以破换成链，再加上那条边，显然我们可以经过或者不经过那条边。

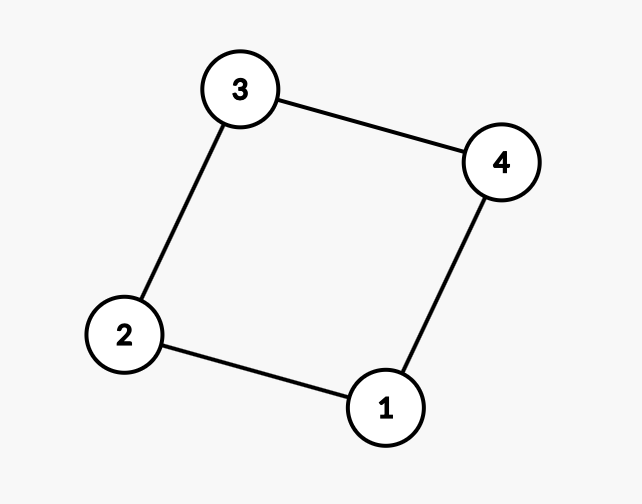
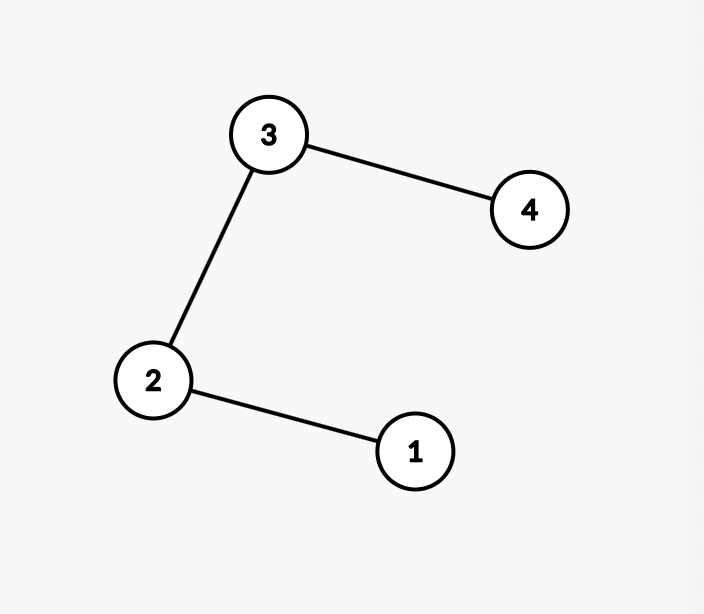
不妨另破换成链的第一个点编号为\(1\)，第二个点编号为\(2\)，我们可以与处理出来一个前缀和表示第一个点到第\(i\)个点的距离\(s_i\)
那么对于\((j->i)\)规定\((j < i)\) 那么其中一条路径长度即为\(s_i - s_j\)
把删去的边加回来发现又多了条路径假设加回来路径边权为\(w\) 路径总长度为\(len\) 那么新路径长度即为\(len - (s_i - s_j) + w\)
定义\(dp_i\)表示经过\(i\)点的最长路径那么\(dp_i = max(f_i + f_j + max (s_i - s_j, len - s_i + s_j + w))\)
分两种情况套路
\(A.\)

\[s_i - s_j > len - s_i + s_j + w \]

\[dp_i = f_i + s_i + max (f_j - s_j) \]

我们只要维护一个最大的\(f_j - s_j\)就行了用线段树或者单调队列都可以
\(B.\)

\[s_i - s_j <= len - s_i + s_j + w \]

\[dp_i = f_i - s_i + len + w + max (f_j + s_j) \]

我们只要维护一个最大的\(f_j + s_j\)就行了用线段树或者单调队列都可以

思路大概就是这些具体做法详见代码用线段树维护\(g_i = f_i + s_i\) 和 \(h_i = f_i - s_i\)即可时间复杂度为\(O(nlogn)\)

const int N = 1e6 + 7;

struct EDGE {
	int to, next, w;
} edge[N << 1];

struct Segment_Tree {
	ll l, r, dat1, dat2;
} t[N << 3];

int n, E, cnt, id, dfn[N], re[N], g[N], head[N], fa[N];
ll ans, h[N], zxy[N], f[N], dp[N], sum[N];
bool in[N], vis[N];
vector < int > circle[N];

inline void addedge (int u, int v, int w) {
	edge[++E].to = v;
	edge[E].next = head[u];
	edge[E].w = w;
	head[u] = E;
}

inline void dfs (int u, int f, int w) {
	dfn[u] = ++ id;
	vis[u] = true;
	g[u] = w;
	for (int i = head[u]; i; i = edge[i].next) {
		int v = edge[i].to;
		if (v == f) continue;
		if (!dfn[v]) fa[v] = u, dfs (v, u, edge[i].w);
		else if (dfn[v] > dfn[u]) {
			++ cnt;
			re[cnt] = edge[i].w;
			for (int j = v; j != fa[u]; j = fa[j]) {
				circle[cnt].push_back (j);
				in[j] = 1;
			}
		}
	}
}

inline int tree_dp (int u, int fa, int cas) {
	int mx = 0, pre = 0;
	for (int i = head[u]; i; i = edge[i].next) {
		int v = edge[i].to, w = edge[i].w;
		if (v == fa || in[v]) continue;
		int sub = tree_dp (v, u, cas);
		if (sub + w > mx) pre = mx, mx = sub + w;
		else pre = max (pre, sub + w);
	}
	zxy[cas] = max (zxy[cas], pre + mx);
	return f[u] = mx;
}

#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)

inline void build (int p, int l, int r, int sz) {
	t[p].l = l; t[p].r = r;
	if (l == r) {
		t[p].dat1 = h[l] - sum[l >= sz ? l - sz : l];
		t[p].dat2 = h[l] + sum[l >= sz ? l - sz : l];
		return;
	}
	int mid = (l + r) >> 1;
	build (ls(p), l, mid, sz);
	build (rs(p), mid + 1, r, sz);
	t[p].dat1 = max (t[ls(p)].dat1, t[rs(p)].dat1);
	t[p].dat2 = max (t[ls(p)].dat2, t[rs(p)].dat2);
}

inline ll query_1 (int p, int l, int r) {
	if (l <= t[p].l && t[p].r <= r) return t[p].dat1;
	int mid = (t[p].l + t[p].r) >> 1; ll ans = -1ll << 62;
	if (l <= mid)
		ans = max (ans, query_1 (ls(p), l, r));
	if (r > mid)
		ans = max (ans, query_1 (rs(p), l, r));
	return ans;
}

inline ll query_2 (int p, int l, int r) {
	if (l <= t[p].l && t[p].r <= r) return t[p].dat2;
	int mid = (t[p].l + t[p].r) >> 1; ll ans = -1ll << 62;
	if (l <= mid)
		ans = max (ans, query_2 (ls(p), l, r));
	if (r > mid)
		ans = max (ans, query_2 (rs(p), l, r));
	return ans;
}

inline ll work (vector < int > v, int cas) {
	int sz = v.size ();
	ll cur = -INF;
	for (int i = 0; i < sz; i ++ ) h[i + sz] = h[i] = f[v[i]];
	memset (sum, 0, sizeof (sum));
	for (int i = 1; i < sz; i ++ ) sum[i] = sum[i - 1] + g[v[i - 1]];
	ll ans1 = 0;
	memset (dp, -1, sizeof (dp));
	build (1, 0, 2 * sz - 1, sz);
	for (int i = 1; i < 2 * sz; i ++ ) {
		if (i >= sz) {
			dp[i] = max (h[i] + sum[i - sz] + query_1 (1, sz, i - 1), h[i] + sum[sz - 1] + re[cas] - sum[i - sz] + query_2 (1, sz, i - 1));
			dp[i] = max (dp[i], max (h[i] - sum[i - sz] + query_2 (1, max (i - sz + 1, 0ll), sz - 1), h[i] + sum[i - sz] + sum[sz - 1] + re[cas] + query_1 (1, max (i - sz + 1, 0ll), sz - 1)));	
		}
		else {
			dp[i] = max (h[i] + sum[i] + query_1 (1, max (i - sz + 1, 0ll), i - 1), h[i] + sum[sz - 1] + re[cas] - sum[i] + query_2 (1, max (i - sz + 1, 0ll), i - 1));
		}
		cur = max (cur, dp[i]);
	}
	return cur;
}

signed main () {
	read (n);
	for (int i = 1, v, w; i <= n; i ++ ) {
		read (v); read (w);
		addedge (i, v, w);
		addedge (v, i, w); 
	}
	for (int i = 1; i <= n; i ++ ) if (!vis[i]) dfs (i, -1, 0);
	for (int i = 1; i <= cnt; i ++ ) {
		for (int j = 0, sz = circle[i].size(); j < sz; j ++ ) tree_dp (circle[i][j], -1, i);
	}
	for (int i = 1; i <= cnt; i ++ ) ans += max (zxy[i], work (circle[i], i));
	write (ans); putchar ('\n');
	return 0; 
}

posted @ 2020-01-22 00:16 Hock 阅读(221) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Hock

[学习笔记] 基环树

知识讲解

例题

例题1 最短距离

题面

正解

Code

例题2[IOI2008]Island

题面

正解

公告