[学习笔记] 斜率优化

应用类型

单调队列优化\(dp\) 针对的是\(f_i = max (f_j) + calc (i)\) \(i - r \leq j \leq i - l\) 需要用单调队列维护区间最大值 类似于滑动窗口的操作 过滤不必要的决策

斜率优化\(dp\)的题目 针对的是\(f_i = max (f_j + calc (j, i))\) 常用单调队列维护决策点或者二分找到最优的决策点

知识讲解

例题1

共有\(n\)个玩具,每个玩具长度\(c_i\)​将\(i~j\)连续的玩具放入一个容器\(i < j\)其长度 \(x = j - i + \sum_{k=j}^i c_k\)制作一个容器的费用为\((x-l)^2\)其中\(L\)为常数.求将所有玩具都放入容器中的费用最小值.

部分分

容易想出状态转移方程式
\(sumc_i\)表示\(\sum_{j = 1}^i c_j\)

\[f_i = min (f_j + (sumc_i - sumc_j + i - j - l)^2) \]

时间复杂为\(O(n ^ 2)\)

优化

为了方便表示 我们可以用\(s_i = sumc_i + i\)

\[f_i = min (f_j + (s_i - s_j - l) ^ 2) \]

将\((s_i - s_j - l) ^ 2\) 拆开

\[f_i = min (f_j + s_i * s_i - 2 * s_i * (s_j + l) + (s_j + l) * (s_j + l)) \]

假设\(j\)为\(i\)的最优决策点

\[f_i =f_j + s_i * s_i - 2 * s_i * (s_j + l) + (s_j + l) * (s_j + l)) \]

将与\(i, j\)都有关的一项放在右边 \(f_i\) 放在右边 其他放在左边

\[f_j + s_i * s_i + (s_j + l) * (s_j + l) = f_i + 2 * s_i * (s_j + l) \]

\(PS\)(我没有将\(l\)移项过去 应为比较懒)
可以用\(y = kx + b\)的形式表示一下方程式
直线过\((s_j + l, f_j + s_i * s_i + (s_j + l) * (s_j + l))\)点 斜率\(k\)为\(2*s_i\) 截距\(b\)为\(f_i\)
如果我们想用\(j\)来转移\(i\)的话，就要让斜率为\(2 * s_i\)的直线过点\((s_j + l, f_j + s_i * s_i + (s_j + l) * (s_j + l))\)并且此时直线的截距就是新的\(f_i\)因为\(f_i\)为这条直线的\(b\)再看下面的图解，我们将求过的点都标到平面直角坐标系中，我们可以发现，我们想过的这个点一定在我们维护的大圆包上，像点2这样的点就不能被用来更新，因为过点3所得截距，一定比过点2所得截距小，那么我们能发现当点3求出之后，只要比较一下，点2和点3形成的直线的斜率和点1和点2形成的直线的斜率，如果2、3形成的比1、2形成的要小，那么3号点一定比2号点更优。我们再看，假设下图之中已经维护好1到5的所有点，那么就会出现这样的大圆包。我们用求出6的点的直线去和这些点相交，我们发现只有点4在当前直线上时能使截距最小（画一画图就能发现是过点4时，直线的截距最小），根据是由点4转移，我们可以发现，当两个点1、3的斜率小于\(2 * s_i\)的时候，横坐标小的点一定不能用来转移，同理斜率大于\(2*s_i\)的两个点，横坐标大的也不能够用来转移，这个性质是不是很好？

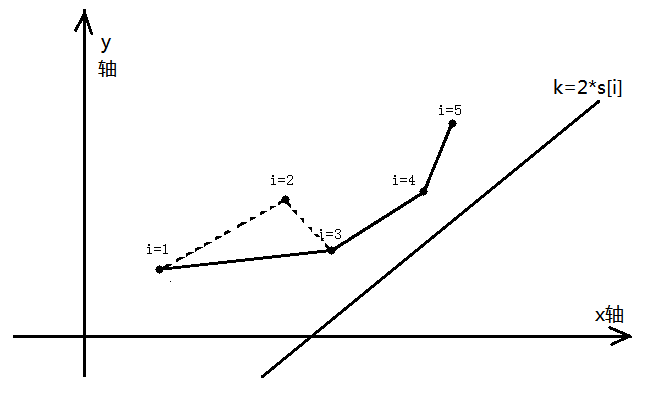
又因为\(s_i\)单调递增 所以我们只要维护一个斜率单调递增的决策点 用单调队列维护即可
对于当前的两个决策点\(j, k\) 斜率为$ (f_j - f_k + (s_j + l) * (s_j + l) - (s_k + l) * (s_k + l)) / (2.0 * (s_j - s_k))\( 对于当前的点\)i$ 我们只要在单调队列找到第一个斜率比\(2*s_i\)大的点即可

Code

inline ll GetSlope (int j, int k) {
	return (double) (f[j] - f[k] + (s[j] + l) * (s[j] + l) - (s[k] + l) * (s[k] + l)) / (2.0 * (s[j] - s[k]));
}
for (int i = 1; i <= n; i ++ ) {
	while (head < tail && GetSlope (q[head], q[head + 1]) <= s[i]) head ++ ;
	f[i] = f[q[head]] + (s[i] - s[q[head]] - l) * (s[i] - s[q[head]] - l); 
	while (head < tail && GetSlope (q[tail - 1], i) < GetSlope (q[tail - 1], q[tail])) tail -- ; 
    q[++tail] = i;
}

模板题目

[HNOI2008]玩具装箱TOY
[USACO08MAR]土地征用Land Acquisition
[APIO2010]特别行动队
[APIO2014]序列分割
[SDOI2016]征途
P3437 小p的牧场
P3156 防御准备