[HNOI2018]道路(DP)

题目描述

W 国的交通呈一棵树的形状。W 国一共有$n-1$ 个城市和$n$ 个乡村，其中城市从$1$ 到$n-1$ 编号，乡村从$1$ 到$n$ 编号，且$1$ 号城市是首都。道路都是单向的，本题中我们只考虑从乡村通往首都的道路网络。对于每一个城市，恰有一条公路和一条铁路通向这座城市。对于城市i， 通向该城市的道路（公路或铁路）的起点，要么是一个乡村，要么是一个编号比$i$ 大的城市。 没有道路通向任何乡村。除了首都以外，从任何城市或乡村出发只有一条道路；首都没有往 外的道路。从任何乡村出发，沿着唯一往外的道路走，总可以到达首都。

W 国的国王小 W 获得了一笔资金，他决定用这笔资金来改善交通。由于资金有限，小 W 只能翻修$n-1$ 条道路。小 W 决定对每个城市翻修恰好一条通向它的道路，即从公路和铁 路中选择一条并进行翻修。小 W 希望从乡村通向城市可以尽可能地便利，于是根据人口调 查的数据，小 W 对每个乡村制定了三个参数，编号为$i$ 的乡村的三个参数是$a^i$ ，$b^i$ 和$c^i$ 。假设 从编号为$i$ 的乡村走到首都一共需要经过$x$ 条未翻修的公路与$y$ 条未翻修的铁路，那么该乡村 的不便利值为

$$c^i\cdot (a^i+x)\cdot (b^i+y)$$

在给定的翻修方案下，每个乡村的不便利值相加的和为该翻修方案的不便利值。 翻修$n-1$ 条道路有很多方案，其中不便利值最小的方案称为最优翻修方案，小 W 自然 希望找到最优翻修方案，请你帮助他求出这个最优翻修方案的不便利值。

输入输出格式

输入格式：

第一行为正整数$n$ 。

接下来$n-1$ 行，每行描述一个城市。其中第$i$ 行包含两个数$s^i,t^i$ 。$s^i$ 表示通向第$i$ 座城市 的公路的起点，$t^i$ 表示通向第i座城市的铁路的起点。如果$s^i>0$ ，那么存在一条从第$s^i$ 座城 市通往第$i$ 座城市的公路，否则存在一条从第$-s^i$ 个乡村通往第i座城市的公路；$t^i$ 类似地，如 果$t^i>0$ ，那么存在一条从第$t^i$ 座城市通往第i座城市的铁路，否则存在一条从第$-t^i$ 个乡村通 往第$i$ 座城市的铁路。

接下来$n$ 行，每行描述一个乡村。其中第i行包含三个数$a^i,b^i,c^i$ ，其意义如题面所示。

输出格式：

输出一行一个整数，表示最优翻修方案的不便利值。

输入输出样例

输入样例#1：复制

6 
2 3 
4 5 
-1 -2 
-3 -4 
-5 -6 
1 2 3 
1 3 2 
2 1 3 
2 3 1 
3 1 2 
3 2 1

输出样例#1：复制

54

输入样例#2：复制

9 
2 -2 
3 -3 
4 -4 
5 -5 
6 -6 
7 -7 
8 -8 
-1 -9 
1 60 1 
1 60 1 
1 60 1 
1 60 1 
1 60 1 
1 60 1 
1 60 1 
1 60 1 
1 60 1

输出样例#2：复制

548

输入样例#3：复制

12 
2 4 
5 3 
-7 10 
11 9 
-1 6 
8 7 
-6 -10 
-9 -4
-12 -5 
-2 -3 
-8 -11 
53 26 491 
24 58 190 
17 37 356 
15 51 997 
30 19 398 
3 45 27 
52 55 838 
16 18 931 
58 24 212 
43 25 198 
54 15 172 
34 5 524

输出样例#3：复制

5744902
 

说明

【样例解释 1】

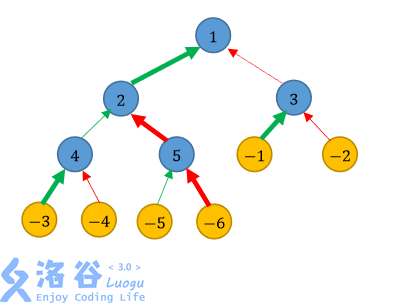
如图所示，我们分别用蓝色、黄色节点表示城市、乡村；用绿色、红色箭头分别表示 公路、铁路；用加粗箭头表示翻修的道路。

一种不便利值等于54的方法是：翻修通往城市2和城市5的铁路，以及通往其他城市的 公路。用→和⇒表示公路和铁路，用∗→和∗⇒表示翻修的公路和铁路，那么：

编号为1的乡村到达首都的路线为：-1 ∗→ 3 ⇒ 1，经过0条未翻修公路和1条未翻修铁 路，代价为3 × (1 + 0) × (2 + 1) = 9；
编号为2的乡村到达首都的路线为：-2 ⇒ 3 ⇒ 1，经过0条未翻修公路和2条未翻修铁 路，代价为2 × (1 + 0) × (3 + 2) = 10；
编号为3的乡村到达首都的路线为：-3 ∗→ 4 → 2 ∗→ 1，经过1条未翻修公路和0条未 翻修铁路，代价为3 × (2 + 1) × (1 + 0) = 9；
编号为4的乡村到达首都的路线为：-4 ⇒ 4 → 2 ∗→ 1，经过1条未翻修公路和1条未翻 修铁路，代价为1 × (2 + 1) × (3 + 1) = 12；
编号为5的乡村到达首都的路线为：-5 → 5 ∗⇒ 2 ∗→ 1，经过1条未翻修公路和0条未 翻修铁路，代价为2 × (3 + 1) × (1 + 0) = 8；
编号为6的乡村到达首都的路线为：-6 ∗⇒ 5 ∗⇒ 2 ∗→ 1，经过0条未翻修公路和0条未翻修铁路，代价为1 × (3 + 0) × (2 + 0) = 6；

总的不便利值为9 + 10 + 9 + 12 + 8 + 6 = 54。可以证明这是本数据的最优解。

【样例解释 2】

在这个样例中，显然应该翻修所有公路。

【数据范围】 一共20组数据，编号为1 ∼ 20。 对于编号$\le 4$ 的数据，$n\le 20$ ；
对于编号为5 ∼ 8的数据，$a^i,b^i,c^i\le 5$ ，$n\le 50$ ；
对于编号为9 ∼ 12的数据，$n\le 2000$ ；
对于所有的数据，$n\le 20000$ ，$1\le a^i,b^i\le 60$ ，$1\le c^i\le 10^9$ ，$s^i,t^i$ 是$[-n,-1]\cup (i,n-1]$ 内的整数，任意乡村可以通过不超过40条道路到达首都。

本以为必有高论。

有个鬼啊！

普及DP入门题套一个废话极多的题面就往HNOI里出。

不想多说。

下面是考场程序，数据分治都没删，把数组范围改一下就A了，考场20，无语。

#include<cstdio>
#include<algorithm>
#define rep(i,l,r) for (register int i=l; i<=r; i++)
typedef long long ll;
using namespace std;

const int N=40010;
const ll inf=100000000000000000;
int n,x,y,fa[N],w[N],l1[N],l2[N],ch[N][2],a[N],b[N],c[N];
ll ans,f[N>>1][41][41];

void jud(){
    ll res=0;
    rep(i,0,n-1){
        int x=0,y=0;
        for (int t=i+n; fa[t]; t=fa[t]){
            if (w[t]==0) x++;
            if (w[t]==2) y++;
        }
        res+=1ll*c[n+i]*(a[n+i]+x)*(b[n+i]+y);
    }
    ans=min(ans,res);
}

void dfs(int dq){
    if (dq==n) { jud(); return; }
    w[ch[dq][0]]^=1; dfs(dq+1); w[ch[dq][0]]^=1;
    w[ch[dq][1]]^=1; dfs(dq+1); w[ch[dq][1]]^=1;
}

void get(int x){
    if (!ch[x][0]) return;
    l1[ch[x][0]]=l1[x]+1; l2[ch[x][0]]=l2[x];
    l1[ch[x][1]]=l1[x]; l2[ch[x][1]]=l2[x]+1;
    get(ch[x][0]); get(ch[x][1]);
}

ll get(int x,int i,int j){ return (ch[x][0]) ? f[x][i][j] : 1ll*c[x]*(a[x]+i)*(b[x]+j); }

void DP(int x){
    if (!ch[x][0]) return;
    DP(ch[x][0]); DP(ch[x][1]);
    rep(i,0,l1[x]) rep(j,0,l2[x])
        f[x][i][j]=min(get(ch[x][0],i,j)+get(ch[x][1],i,j+1),get(ch[x][0],i+1,j)+get(ch[x][1],i,j));
}

int main(){
    freopen("road.in","r",stdin);
    freopen("road.out","w",stdout);
    scanf("%d",&n);
    if (n<=20){
        rep(i,1,n-1){
            scanf("%d%d",&x,&y);
            if (x<=0) x=-x+n-1; if (y<=0) y=-y+n-1;
            ch[i][0]=x; ch[i][1]=y; fa[x]=fa[y]=i; w[x]=0; w[y]=2;
        }
        rep(i,0,n-1) scanf("%d%d%d",&a[n+i],&b[n+i],&c[n+i]);
        ans=inf; dfs(1); printf("%lld\n",ans);
    }else{
        rep(i,1,n-1){
            scanf("%d%d",&x,&y);
            if (x<=0) x=-x+n-1; if (y<=0) y=-y+n-1;
            ch[i][0]=x; ch[i][1]=y; fa[x]=fa[y]=i; w[x]=0; w[y]=2;
        }
        rep(i,0,n-1) scanf("%d%d%d",&a[n+i],&b[n+i],&c[n+i]);
        get(1); DP(1); printf("%lld\n",f[1][0][0]);
    }
    return 0;
}