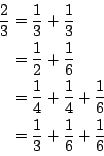[POJ1980]Unit Fraction Partition(搜索)

Unit Fraction Partition

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 4571		Accepted: 1809

Description

A fraction whose numerator is 1 and whose denominator is a positive integer is called a unit fraction. A representation of a positive rational number p/q as the sum of finitely many unit fractions is called a partition of p/q into unit fractions. For example, 1/2 + 1/6 is a partition of 2/3 into unit fractions. The difference in the order of addition is disregarded. For example, we do not distinguish 1/6 + 1/2 from 1/2 + 1/6.

For given four positive integers p, q, a, and n, count the number of partitions of p/q into unit fractions satisfying the following two conditions.

The partition is the sum of at most n many unit fractions.
The product of the denominators of the unit fractions in the partition is less than or equal to a.
For example, if (p,q,a,n) = (2,3,120,3), you should report 4 since

enumerates all of the valid partitions.

Input

The input is a sequence of at most 200 data sets followed by a terminator.

A data set is a line containing four positive integers p, q, a, and n satisfying p,q <= 800, a <= 12000 and n <= 7. The integers are separated by a space.

The terminator is composed of just one line which contains four zeros separated by a space. It is not a part of the input data but a mark for the end of the input.

Output

The output should be composed of lines each of which contains a single integer. No other characters should appear in the output.

The output integer corresponding to a data set p, q, a, n should be the number of all partitions of p/q into at most n many unit fractions such that the product of the denominators of the unit fractions is less than or equal to a.

Sample Input

2 3 120 3
2 3 300 3
2 3 299 3
2 3 12 3
2 3 12000 7
54 795 12000 7
2 3 300 1
2 1 200 5
2 4 54 2
0 0 0 0

Sample Output

4
7
6
2
42
1
0
9
3

Source

Japan 2004 Domestic

[Submit]   [Go Back]   [Status]   [Discuss]

沦落到要做普及组题目的地步了吗。。发现自己连搜索都不会写了。

几个可行性剪枝就可以了：乘积不超限，个数不超限，分数和不超过目标。

起先一直TLE，把循环中的除法提到外面就卡过了。

这种题目竟然也要做1h。。

#include<cstdio>
#include<algorithm>
#define rep(i,l,r) for (int i=l; i<=r; i++)
using namespace std;

int p,q,a,n,ans;

void dfs(int mn,int num,int deno,int mul,int dq){
    if (mul>a) return;
    if (num*q==deno*p) ans++;
    if (num*q>deno*p || dq==n) return;
    int t=a/mul;
    rep(i,mn,t) dfs(i,num*i+deno,deno*i,mul*i,dq+1);
}

int main(){
    freopen("poj1980.in","r",stdin);
    freopen("poj1980.out","w",stdout);
    while (~scanf("%d%d%d%d",&p,&q,&a,&n)){
        if (q==0) return 0;
        ans=0; dfs(1,0,1,1,0); printf("%d\n",ans);
    }
    return 0;
}