时间序列分析建模步骤及Python实现
平稳时间序列的意义
根据数理统计学常识,要分析的随机变量获得的样本信息越多,分析的结果就会越可靠,但由于时间序列分析的特殊数据结构,对随机序列{...,X1,X2...,Xt,...}而言,它在任意时刻 t 的序列值 Xt 都是一个随机变量,而且由于时间的不可重复性,该变量在任意一个时刻都只能获得唯一的样本观察值,通常是没有办法分析的。在平稳序列场合里,序列的均值等于常数,意味着原本含有可列多个随机变量的均值序列变成了一个常数序列,原本每个随机变量的均值只能依靠唯一的一个样本观察值去估计,现在每一个样本观察值都变成了常数均值的样本观察值,这极大的减少了随机变量的个数,并增加了待估参数的样本容量。
平稳性校验
- 一种是根据时序图和自相关图显示的特征做出判断的图检验方法(自相关图是一个平面二维坐标悬垂线图,一个坐标轴便是延迟时期数,另一个坐标轴表示自相关系数,通常以悬垂线表示自相关系数的大小。自相关图进行平稳性判断的标准:随着延迟期数 k 的增加,平稳序列的自相关系数会很快的衰减向零;反之,非平稳序列的自相关系数衰减向零的速度通常比较慢)
import numpy as np
import pandas as pd
from datetime import datetime
import matplotlib.pylab as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
#读取原始时间序列数据
df=pd.read_csv('wq.csv',encoding='utf-8', index_col='datatime') #从csv文件中读取时间序列数据,index_col列定义为索引对象
df.index=pd.to_datetime(df.index)
ts=df['dataColumn'] #指定时间序列中对应的数据列
ts.head()
ts.head().index
ts=ts.dropna() #去除掉时间序列中的空值,否则无法绘制出正常的acf图
#输出原始序列
f = plt.figure(facecolor='white')
ts.plot(color='blue', label='Original')
plt.title('TimeSeries Original Data')
plt.show()
#输出ACF(自相关图)、PACF(偏自相关图)
f = plt.figure(facecolor='white')
ax1 = f.add_subplot(211)
plot_acf(ts, lags=31, ax=ax1)
ax2 = f.add_subplot(212)
plot_pacf(ts, lags=31, ax=ax2)
plt.show()
- 另一种是构造检验统计量进行假设检验的方法(目前最常用的平稳性统计校验方法是单位根检验,DF检验和ADF检验)DF检验只适合1阶自回归过程的平稳性检验,ADF检验是对DF检验做了一个修正,得到增广DF检验(augrmented Dickey-Fuller)。一般认为检验结果p值<0.05时,认为检验序列为平稳时间序列
from statsmodels.tsa.stattools import adfuller
#adf校验
ts=ts[~ts.isin(['null'])] #去除时间序列中值为空的行
ts=ts.dropna() #去除掉所有NaN值
dftest = adfuller(ts) #ADF校验
# 对上述函数求得的值进行语义描述
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print(dfoutput) #输出df校验结果
数据预处理
通过平稳性校验,序列可以分为平稳序列和非平稳序列,对于非平稳序列,通常要进行进一步的校验、变换或处理后,才能确定合适的拟合模型;变化处理方式包含对数变化、差分变换、拆分处理等。
对数变换主要是为了减小变化较大的时序数据的振动幅度,使其线性规律更加明显
#对数变换
ts_log = np.log(ts)
#对数变换后的序列输出
f = plt.figure(facecolor='white')
ts_log.plot(color='blue', label='log Data')
plt.title('TimeSeries log Data')
plt.show()
平滑法:根据平滑技术的不同,平滑法分为移动平均法和指数平均法,移动平均即利用一定时间间隔内的平均值作为某一期的估计值,而指数平均则是用变权的方法来计算均值,认为离着预测点越近的点,作用越大。
- 简单中心移动平均能有效消除季节效应,有效提取低阶趋势,能实现拟合方差最小
- 简单移动平均比值能有效提取季节效应
# 对size个数据进行移动平均 rol_mean = timeSeries.rolling(window=size).mean() # 对size个数据进行加权移动平均 rol_weighted_mean = pd.ewma(timeSeries, span=size) rol_mean.dropna(inplace=True) rol_weighted_mean.dropna(inplace=True)
差分运算,(预测方法中并没有解决高于2阶的差分)经过差分运算后的序列,呈现典型的随机波动特征。差分方法的优点是对确定性信息的提取比较充分,缺点是很难对模型进行直观解释(当序列具有非常显著的确定性趋势或者季节效应时,为了通过确定性因素分解方法提取序列中各种确定性效应的解释,构造了残差自回归模型)
- 序列蕴涵显著的线性趋势,1阶差分就可以实现趋势平稳
- 序列蕴涵曲线趋势,通常低阶(2阶或者3阶)差分就可以提取出曲线趋势的影响
- 蕴涵固定个周期的序列,进行步长为固定周期长度的差分运算,可以较好的提取周期信息
#差分计算 ts_diff1=ts.diff(1) ts_diff2=ts.diff(2) #输出时间序列 f = plt.figure(facecolor='white') ts.plot(color='green', label='原始数据') ts_diff1.plot(color='blue', label='1阶差分') ts_diff2.plot(color='red', label='2阶差分') plt.show()
拆分:使用确定性因素分解方法。所有的序列波动都可以归纳为受长期趋势、循环趋势、季节性变化、随机波动4大类因素的综合影响,也就是说任何一个时间序列都可以用这4个因素的某个函数进行拟合,最常用的函数是加法函数和乘法函数
from statsmodels.tsa.seasonal import seasonal_decompose decomposition = seasonal_decompose(ts, model="additive",period=6) trend = decomposition.trend #趋势序列 seasonal = decomposition.seasonal #季节序列 residual = decomposition.resid #随机序列
白噪声检验
对于平稳序列,只有那些序列值之间具有密切的相关关系,历史数据对未来发展有一定影响的序列,才值得建模。(如果序列彼此之间没有任何相关性,那就意味着该序列是一个没有记忆的序列,过去的序列对未来的发展没有任何影响,是一种没有任何分析价值的而序列,称之为纯随机序列,白噪声序列就是一种纯随机序列)
Barlett证明,如果一个时间序列是纯随机的,得到一个观察期数为n的观察序列,那么该序列的延迟非零期的样本自相关系数将近似服从均值为0,方差为序列观察期数倒数的正态分布。
我们假设序列为纯随机的,即延迟期数小于或等于m期的序列值之间相互独立(不相关)。使用Q统计量和LB统计量来校验白噪声序列,计算出Q统计量的p值之后,如果p值大于0.05,就说明我们无法拒绝原假设(该序列是白噪声序列),这个时间序列的确就是白噪声序列。
- Q统计量:Q统计量近似服从自由度为m的卡方分布,当Q统计量大于卡方分位点或者统计量的P值小于α时,则可以以1-α的置信水平拒绝原假设,认为该序列为非白噪声序列,否则,不能拒绝原假设,认为该序列为纯随机序列。在大样本场合,检验效果很好,但在小样本场合不太精确
- LB统计量:是对Q统计量的修正,同样近似服从自由度为m的卡方分布,在各种检验场合,普遍采用的Q统计量通常指的都是LB统计量
from statsmodels.stats.diagnostic import acorr_ljungbox p_value = acorr_ljungbox(ts,lags=[6,12]) #lags可自定义,一般取第6和第12延迟期数,这是因为平稳序列通常具有短期相关性,如果序列值之间存在显著的相关关系,通常只存在于延迟期间比较短的序列值之间。 print(p_value)
acorr_ljungbox(ts, lags=None, boxpierce=False)函数检验无自相关函数输入输出说明
输入值:
lags为延迟期数,如果为整数,则是包含在内的延迟期数,如果是一个列表或数组,那么所有时滞都包含在列表中最大的时滞中
boxpierce为True时表示除开返回LB统计量还会返回Box和Pierce的Q统计量
返回值:
lbvalue:测试的统计量
pvalue:基于卡方分布的p统计量
bpvalue:((optionsal), float or array) – test statistic for Box-Pierce test
bppvalue:((optional), float or array) – p-value based for Box-Pierce test on chi-square distribution
模型选择
常见模型包括AR(自回归模型)、MA(移动平均模型)、ARMA(自回归移动平均模型)、ARIMA(求和自回归移动平均模型)。模型选择的一项重要工作是确定p,q 的阶数。
一种通过对平稳时间序列的自相关系数(ACF)和偏自相关系数(PACF)的计算,绘制自相关图和偏自相关图,通过拖尾、截尾性质,确定合适的模型以及各自阶数。
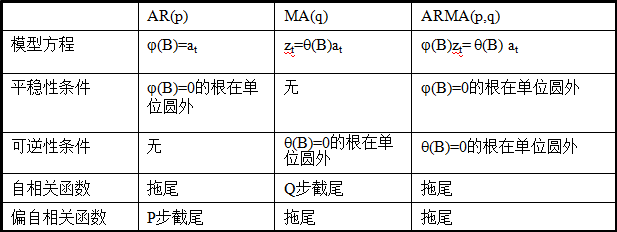
另一种通过借助AIC、BIC统计量自动确定
##借助AIC、BIC统计量自动确定
from statsmodels.tsa.arima_model import ARMA
def proper_model(data_ts, maxLag):
init_bic = float("inf")
init_p = 0
init_q = 0
init_properModel = None
for p in np.arange(maxLag):
for q in np.arange(maxLag):
model = ARMA(data_ts, order=(p, q))
try:
results_ARMA = model.fit(disp=-1, method='css')
except:
continue
bic = results_ARMA.bic
if bic < init_bic:
init_p = p
init_q = q
init_properModel = results_ARMA
init_bic = bic
return init_bic, init_p, init_q, init_properModel
调用自定义函数
#调用自定义方法 proper_model(trainSeting,40)
ARIMA模型的实质就是差分运算与ARMA模型的组合。这一关系意义重大。这说明任何非平稳序列如果能通过适当阶数的差分实现差分后平稳,就可以对差分后序列进行ARMA模型拟合了
from statsmodels.tsa.arima_model import ARIMA model=ARIMA(data,order=(p,d,q)).fit()
参数估计
- 矩估计
- 极大似然估计(必须已知总体的分布函数,在时间序列分析中,序列总体的分布通常是未知的,为便于分析和计算,通常假设序列服从多元正态分布)
- 最小二乘估计(在实际中,最常用的是条件最小二乘估计方法)
模型检验
模型检验包括模型的显著性校验和参数的显著性校验
- 模型的检验即为残差序列中的白噪声检验,如果残差序列是白噪声序列,则拟合残差项中将不蕴涵任何相关信息,即模型提取的信息足够充分,模型的显著性高;反之,说明模型拟合不够有效,需要选择其他模型,重新拟合
- 参数的显著性校验就是要检验每一个未知参数是否显著非零。检验的目的是使模型最精简
模型优化
综合考虑模型的拟合精度和未知参数个数的综合最优配置。若一个拟合模型通过了校验,说明在一定的置信水平下,该模型能有效拟合观察值序列的波动,但这种有效模型不一定是唯一的。在所有通过校验的模型中使用AIC或者SBC函数达到最小的函数为相对最优模型。
参考资料:中国人民大学出版社《应用时间序列分析》第四版 王燕编著



 浙公网安备 33010602011771号
浙公网安备 33010602011771号