[线性代数] 矩阵代数基础 Basic Matrix Algebra

Overview: Matrix algebra

Matrix algebra covers rules allowing matrices to be manipulated algebraically via addition, subtraction, multiplication and division. However, despite the manipulations illustrated in the following may seem to be like that of normal algebra, bear in mind that for everything we do in matrix algebra, we consider the manipulation of LINEAR COMBINATION, not individual elements in matrices. The difference would help rationalize many properties below. So, please bear in mind of this.

 

Matrix addition

When doing matrix addition, we have a requirement that all matrices being added along the way should be of same sizes. This requirement can be proved as the following: since all matrices having same size must have their columns in same size with each other as well. Thus, a_j+b_j+c_j+…+n_j = y_j stands for all columns within the addition chain. Nothing special, everything simple enough.

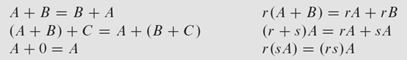
Matrix multiplication

While matrix multiplication does not involve the too-restrictive 'same size' assumption as that in matrix addition and subtraction, it still requires size of rows of preceding matrix = size of column of the matrix followed.

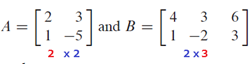
Noted that matrix multiplication is NOT COMMUNTATIVE, meaning 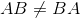, a scratch of proof as follow:

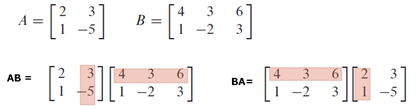
Indeed, matrix multiplication is like matrix-vector multiplication as follows. In Ab_i, each column on RHS matrix acts as a coefficient to the matrix comes before it, which means each element in b_i acts as a coefficient to each column in A.

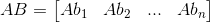
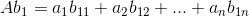
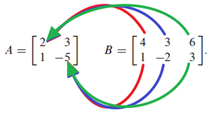
Sometimes in matrix multiplication, it's quite hard to recall to which element in the resulting matrix will the current operation result go. Fortunately, we have the row-column rules, which states each row of multiplicand corresponds to each row in resulting matrix after some linear combination.

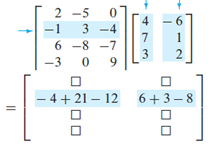
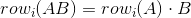
Another mnemonic to help us remember the order :D

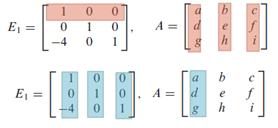
So we have the following 'seemingly trivial' matrix multiplication rules, but they are all reasonable. Noted that despite matrix multiplication is both left and right distributive, they are not commutative! Order must be strictly observed so the assumption of 'size of row of multiplicand = size of columns in multiplier' is upheld. Moreover, such non-commutativity also renders a dimensionality transformation of identity matrix in I_mA=AI_n.

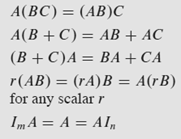
Some sketches of proofs in terms of columns. Noted that (B+C) is essentially element-wise operations, which should not affect linear combination much.

    

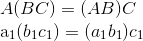
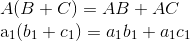
Finally, there are few warnings about matrix multiplication. As mentioned, always bear in mind matrix multiplication is completely different from real-number multiplication, in a sense that the former considers the linear combination among columns in multiplicands weighted by elements in multiplier. Thus, we yield the following reminders about matrix multiplication:

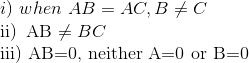
Another aspect of matrix multiplication is matrix power, where matrices multiplied by themselves. Due to the chaining nature of matrix power, it requires each A to be of nxn square matrix.

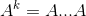
In the following, I'm going to introduce matrix transpose, which application is not yet explicit for the moment. Transposing a matrix allows the interchange of dimension of a matrix. Imagine a 3x2 matrix B, B^T becomes 2x3. It sometimes become handy in matrix multiplication, like:

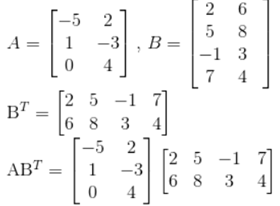
Matrix inverse

Warning: matrix inverse refers to any invertible matrices not limited to 2x2! Just that the calculation of invertibility of larger matrix is a little bit more involved. Interested readers may refer to here. Thus, the properties below actually apply to larger matrix.

A non-singular matrix must be of nxn. Its inverse must be uniquely determined. Noted here that 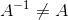, and the LHS and RHS of the following must be satisfied simultaneously. Otherwise, the matrix A can only be a singular matrix. This highlights the important property of matrix multiplication, that left multiply and right multiply do make a difference. This also justify why the nxn requirement for matrix to be invertible.

 

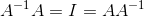
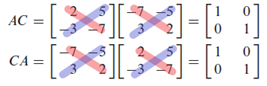
We can conclude from below that indeed A^-1 = C. Moreover, when observed closely the relation between the colored stripes above, we can draw inference about what determines a matrix to be invertible or not by simple inspection of the matrix we are interested in. In general, a invertible matrix satisfies:

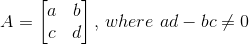
So, from above, 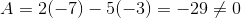, A is invertible. Noted still, we have zero idea about who is its invertible. So the following formula comes into rescue:

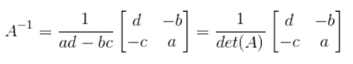
With the uniqueness of matrix inverse, we can answer the uniqueness problem of a matrix equation without going through the pain of row-reduction algorithm: for any nxn invertible matrix, Ax=b must have unique solution. A sketch of proof would be that A^-1A=I, and identity matrix has no free variable and always have a pivot position at each column. This gives unique solution.

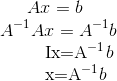
Below show some properties of invertible matrices:

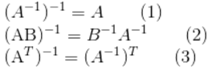
(2) states if A and B are both invertible nxn matrices, AB is also invertible and its inverse is B^-1A^-1 .

Proof of (2):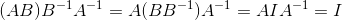

Proof of (3): 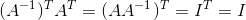. And that if A is invertible, so is A^T.

 

Elementary Matrix

It refers to an identity matrix I_n being applied a SINGLE row operation. Recalled the painful row operation to be performed when we need to row-reduce a matrix. Such trouble can be effectively avoided by multiplying elementary matrix onto the matrix A being row-reduced. Instead of directly applying row operations onto A, we apply it on identity matrix I, one at a time. As we know to get the reduced row echelon form of A, we have to undergo a series of row operations. This means we need to apply row operations onto a series of identity matrices before left-multiplying them on A, as follows:

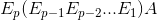
Since row operation does not change the solution set of a matrix equation, 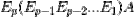is row equivalent to A!

Recall that row operations are reversible and let E' denotes the reverse of row operation, we have IA=A:

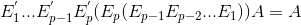
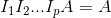
This sounds familiar…doesn't it mean that elementary matrices are invertible? Indeed, find E' is equivalent of finding E^-1. Unfortunately, our discussion of invertibility above only limited to 2x2. Then how can we invert a nxn matrix in general?

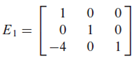
Despite it can be as computationally involved as illustrated in the link above, finding an inverse on E can be trivial. You can simply tell what row operation has been applied onto I to generate E1 above. Thus, we have the following:

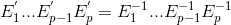
Matrix A is invertible (AA^-1=A^-1A=I_n) if it can be row-reduced to I_n. And we claim that any sequence of elementary row operations reducing A to I_n also transform I_n to A^-1. Assuming A is invertible, a sketch of proof as follow:

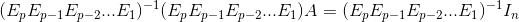
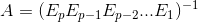
Thus, we have:

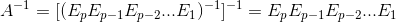
This has great implication, as we know in general,

But now we can apply the elementary matrices WITH SAME SEQUENCE on A to transform:

1. A to I_n
2. I_n to A^-1

If you are just given a matrix A, how could you test if inverse exists? How to find one? Recalled from above invertibility means that:

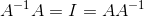
And we also use determinants to test and find the inverse of 2x2 matrices. We also have that complicated procedure for dealing with matrix beyond 2x2. But from our discussion immediately above, we seem to find another way of dealing with nxn invertibility without going through the plain of that complex algorithm.

Why not putting them all together to get [A I], on which a sequence of elementary matrices is applied to yield [I A^-1]? If the nxn matrix A does not have an inverse, [A I] cannot be row reduced to [I A^-1]. Sometimes only certain column of A^-1 is needed, we can even solve [A e_i] instead of [A I] as we know [A I] = [A e₁ e₂ … e_n].

 

Characteristics of invertible matrices

Most of you may encounter the lengthy list of invertible properties when studying invertible matrices. However, everything can be boiled down into the following:

invertible == row equivalent to In == n pivot columns == columns all linearly independent == columns span Rn == linear transformation one-to-one for Ax=0 == at least one solution to Ax=b (at least have that for Ax=0)

However, there still one tricky property which requires some derivation:

The linear transformation x à Ax maps Rⁿ to Rⁿ

Let's consider the proof as follows: as A is invertible, A must be a nxn and all columns thus span Rⁿ. Naturally, the above stands.

With these properties at our belt, we can quickly determine if a nxn matrix is invertible or not: when it can be row-reduced to a yield a unique solution/ to be an identity matrix, it must be invertible. After all, invertibility is guaranteed by matrices which are row equivalent to identity matrix.

Despite the universality of these characteristics linking the concepts of linear independence to solution uniqueness, one limitation is that all these only apply on square matrices. For non-square matrices, we still need to painfully row-reduce the matrix to decide the basic and free variables.

 

Invertible linear transformation

Definition first. A linear transformation T: Rⁿ à Rⁿ is invertible

1. iff standard matrix of standard matrix of T, namely A, is invertible. è explains why T need to be Rⁿ à Rⁿ
2. iff there exists a function S: RⁿàRⁿ such the following holds FOR ALL x IN Rⁿ:

S(T(x)) = x

T(S(x)) = x

Noted here we are talking about INVERSE of linear transformation, and the result of the applying the inverse of linear transformation onto another one recovers the input vector x. This becomes useful in solving matrix equations later.

 

If linear transformation T is invertible, S(x)=A^-1x is a unique function satisfying S(T(x)) = x and T(S(x)) = x, namely:

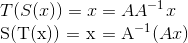
Thus, it's like what we've seen, and S upholds the uniqueness of inverse.

Here, to summarize, we observed that for a linear transformation T: RⁿàRⁿ, the columns of standard matrix must be linearly independent and span across Rⁿ, and thus gives an onto mapping, hence T is an invertible linear transformation and there exists a unique inverse: S(x)=A^-1x, which recovers the input vector x from T(x).

 

Some Examples

後續：例子不定期更新，矩陣代數進階版

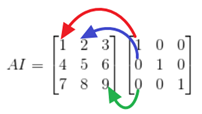
Ex 1. Proof of identity matrix multiplication: AI=A. As you can see, a_i with non-one coefficient are zeroed-out.

Ex 2. Prove when a nxn matrix is invertible, Ax=b exists unique solution for all b belongs to Rⁿ. From the following, we see the uniqueness of solution relies on uniqueness of the inverse, A^-1.

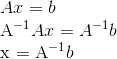
Ex 3. We mentioned that by applying a series of elementary row operations on [A I], we get [I A^-1]. If we are to row-reduce A^-1 back into I again, we must apply the series in an reverse order: 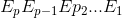. In other words, the same sequence can only be used to reduce A to I and I to A^-1, but not the reverse.

 

Ex 4. When asking about if B=C where AB=BC, we must know if A is invertible or not. If A is invertible, then this B=C stands. Otherwise, it does not.

 

Ex 5. If AB, B is invertible, then A must be invertible. We first let C be the product of the invertible AB. By theorem, since AB invertible, C must be invertible as well. Noted in the final step we get A equals to the product of invertible matrices. Hence A is invertible. ■

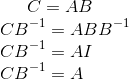
Ex 6. Recalled that for invertible nxn matrix A, for any b in Rⁿ, there exists a unique solution to Ax=b, namely x=A^-1b. Also recall there's a unique sequence {E_i} which transform A to A^-1. This justifies the uniqueness of x. As there's unique solution x to the system, the columns span Rⁿ and we can conclude that for an invertible matrix, columns of A spans Rⁿ and are linearly independent.

 

Ex 7. Careful when we try to row reduce [A I], sometimes A turns out to be singular.

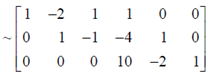
Ex 8. General concepts for nxn matrix A

1. if Ax=0 only has trivial solution, meaning there are only basic variables and thus all columns are pivot columns. Thus, they are linearly independent and reducible to/ row-equivalent to identity matrix.
2. In other words, for a nxn matrix, if there are n pivot positions, it's definitely invertible and has at least one unique solution in Ax=b
3. Recall a nxn matrix A has another nxn matrix D such that AD=I, there must exist a nxn matrix C where CA=I. Specifically, C=D due to inverse uniqueness.
4. A linear transformation T: x à Ax mapping Rⁿ to Rⁿ, i.e. no dimensional changes.
5. When the columns in A are linearly independent, then they spans Rⁿ. Recall definition of linear span of a set of vectors in a vector space. Span is the intersection of ALL linear subspaces each containing every vector within the subspace. Or, schematically, where A,B and C are all vector spaces.

   

   Thus, with n linearly independent columns in a nxn matrix, they must form a basis vector set for Rⁿ, all possible linear combination of these vectors must reconstruct the vector space Rⁿ, thus they 'span' Rⁿ.

6. By the theorem, if there exists at least one solution to Ax=b, then the linear transformation is one-to-one. Noted that if only the former part of the statement is true, there still has chance to be a onto mapping but not one-to-one, if there exists free variable in matrix. But for a nxn matrix with at least one solution to Ax=b, there must be n pivot columns, according to the theorem. Thus, the mapping becomes one-to-one, as it is not possible to have free variables anymore.