关于n维和n-1维欧式空间的理解（转）

转自：https://www.cnblogs.com/stevenlk/p/6497800.html   初学者看了个大概，理解不是很深，故转载以留以后逐渐理解

 

我们从小就说，“点动成线，线动成面，面动成体”，其中的空间的概念到底是啥？之前没有好好想过，在机器学习中多次遇到“空间”、“超平面”，“分割面”等概念，一会n维，一会儿n+1维，理解的有点模糊。今儿突然应该是彻底想明白了，记录一下。
　　
　　先抛出一个问题：x1+x2+2=0请问，是几维空间，对，是二维空间，那是平面，还是直线哪？
　　咦，二维空间，我们通常不是说二维空间是平面吗，但这里，怎么看都是一个直线方程啊。。。怎么理解 x1+x2+2=0 “二维的方程表达的是直线”，但同时通常说“二维平面”这一现象？
　　
　　二维本质是面，是指在两个变量没有任何的约束情况下的任意组合(基坐标的线性组合)a1x1+a2x2=ax 点 (a1,a2)，则所有点的集合即为整个平面。

　　如果，这个线性组合被约束了，比如：x1+x2+2=0，则相当于一个变量能被其他变量的线性组合表达，其本质是只有1个自由变量，所以本质上是被降了一维(n-1维)，所以看起来是二维的自由变量，本质上是一个自由变量，另外一个是因变量，故其本质是一维的“线”。

　　若果令 L=a0+a1x1+a2x2=ax(这里把截距单独拿出来了)，跟则在 L 根据 a的变化，可以表示二维平面中的任意一条直线，从这个角度理解，所有的直线的集合不就构成了面吗。并且，为了形式上的统一，二维空间中的任意一条直线L，可以表达为：a0+a1x1+a2x2=0

形式。

　　在机器学习中，为了将这个 0作为应变量(类别) y的比较对象，将几何意义直线 L的作为代数表达 y=0 ：
　　上面的例子中，若 y 为 x1+x2+2=0 的直线，如果令 y=2则 y=x1+x2+2=2相当于该直线向下平移了2个单位距离，因此在SVM中，本质上使用距离的度量去表示因变量(样本类别)——==整个SVM模型的研究坐标空间只有特征空间(最后一个坐标是第n个自变量xn，不是因变量 y)==。因此，有了 y=x1+x2+2=0 这条直线(超平面)，可以很方便的写出超平面的上下方区域的代数形式：x1+x2+2>0 为下半面，x1+x2+2<0 为直线的上半面——大于0在直线左边，小于0在直线右边。至于到底是上方还是下方，则看直线的斜率——斜率为正，大于0则在上方；否则在下方。
　　
注：
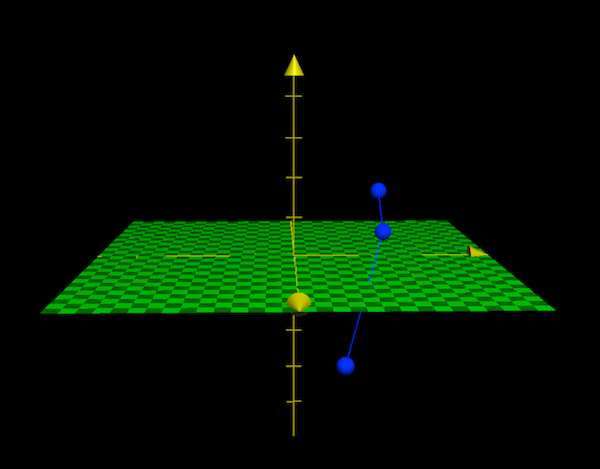
　　由于我们是在二维平面上讨论 y=x1+x2+2 这个三个变量的事情，相当于在将三维空间的事情，放在二维空间上来讨论，用直线位置的变化来表示第三维的变量的取值；如果上升一个坐标维度，放在三维空间内讨论，那么就是正类、负类分别散落在平面y=0

的散点图：

关于隐函数和其求导，这边文章写的挺好，可以看看：
《小谈导数、梯度和极值》