2021.2.7网络流习题总结
2021.2.7网络流习题总结
总是在后一天补前一天的锅,不过没办法,我太菜了,不能像TX他们一样快速AK列表。
1.【模板】最小费用最大流
题目链接: there
由普通的最大流扩展而来,是网络流、二分图中常用的,方法是将找最大流时过程的BFS改为SPFA算法,求最长路,最短路等,有2种写法,一种是用EK为基础的 ,也是最常用的,一般上公开赛出题人都不会毒瘤到去卡它,因为卡它没意义,而且网络流本身也不能处理很大的数据。
方法一:EK:
这里就是在你用BFS求最大流的时候,把BFS改为SPFA,然后在保证最大流的前提下,找出最小花费或者最大花费。其实这个就很简单,但开始写的时候细节还是有一点的,记得反向边的流量仍然为0,不过反向边的费用要设为-的,这是为了让它回去的时候原先走的贡献加起来为0,可以自己认真背诵(大雾)
#include<bits/stdc++.h> #define int long long using namespace std; template<typename T> inline void read(T &x){ T f=1;x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} x*=f; } const int N = 5e5,INF = 2e9; int n,m,s,t,nex[N],first[N],v[N],flow[N],cost[N],num=1; inline void add(int from,int to,int ff,int cos){ nex[++num]=first[from]; first[from]=num; v[num]=to; flow[num]=ff; cost[num]=cos; } queue<int>q; int dis[N],inf[N],pre[N],last[N],vis[N],mxflow,mincost; bool spfa(int s,int t){ memset(dis,0x7f,sizeof(dis)); memset(vis,0,sizeof(vis)); memset(inf,0x7f,sizeof(inf)); q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=first[u];i;i=nex[i]){ int to=v[i]; if(flow[i] && dis[to]>dis[u]+cost[i]){ dis[to]=dis[u]+cost[i]; pre[to]=u; last[to]=i; inf[to]=min(inf[u],flow[i]); if(!vis[to]){ vis[to]=1; q.push(to); } } } } return pre[t]!=-1; } void EK(int s,int t){ while(spfa(s,t)){ int now=t; mxflow+=inf[t]; mincost+=inf[t]*dis[t]; while(now!=s){ flow[last[now]]-=inf[t]; flow[last[now]^1]+=inf[t]; now=pre[now]; } } } signed main(){ read(n),read(m),read(s),read(t); for(int i=1;i<=m;i++){ int u,v,w,c; read(u),read(v),read(w),read(c); add(u,v,w,c); add(v,u,0,-c); } EK(s,t); cout<<mxflow<<" "<<mincost; return 0; }
方法二:zkw算法
不会,没去看,感觉好丑,还要用deque,放个链接,有空补
2.[HAOI2010]订货
题目链接:there
高级的想法,这个不是我自己想到的,卡着了。解法是以月份作为点,成本作为费用,需求作为容量,然后可以单独构建点作为仓库,也可以直接向下连边,就像这样,当然图不是我的,是一位题解区里的大佬的,我搬过来,水一波
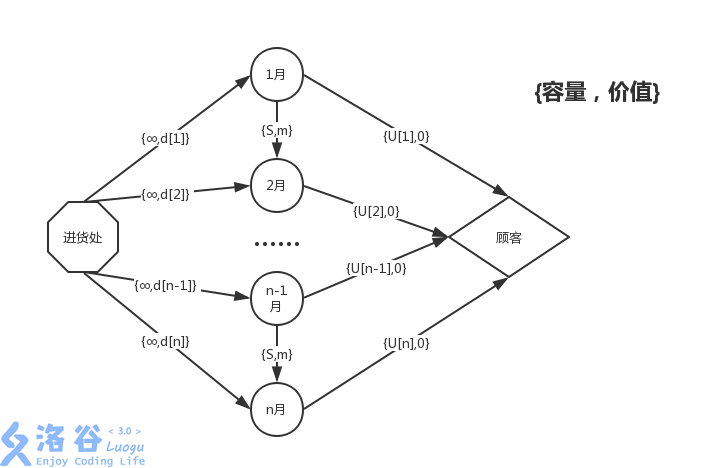
那么看了之后可能就可以很快的写出代码了,毕竟这个就是很快速的事情,只要建好了模,那么就直接套用模板。
于是决定只放一部分代码,EK应该都能写吧QAQ。
read(n),read(m),read(s);//s表示仓库容量 S = 0; T = 9000; for(int i=1;i<=n;i++){ int x; read(x); add(i,T,x,0); add(T,i,0,0); if(i!=n){ add(i,i+1,s,m); add(i+1,i,0,-m); } } for(int i=1;i<=n;i++){ int x; read(x); add(S,i,INF,x); add(i,S,0,-x); } EK(S,T); cout<<mincost<<" ";
3.负载平衡问题
题目链接:there
此题解法有两种,一种是网络流,一种是贪心。。。
解法一:贪心
发现这道题莫名更均分纸牌贼像,首先你可以加上所有值,然后除以n求出所有位置变化后的值,然后这是一个环形的均分纸牌。环形的有几种方法处理,因为这题的数据范围较小,所以你可以将1-n中每个点作为起点,跑一次均分纸牌,常用方法是扩大两倍法。但是其实还有一种神奇的方法,将每个仓库中的货物数变为数列的中位数时,所需的代价最小。能通过此题,但它其实是个假算法,因为这题是环形,建议自己还是用环形均分纸牌的方式跑,常见的环形处理方式也顺便练习了一波。这里就不粘代码了
解法二:网络流
就是这道题属于一种常见的费用流建模类型,我采取的建模方式是首先建立一颗超级源点s,其次建立一颗超级汇点t,然后货物与它相邻的两个货物连边,由于是环形的,所以1和n也要互相连接起来,然后将最后要的状态算出来,如果你的当前位置货物等于所求,那就不搬,即不连边,小于所求,向t连边。大于所求s向当前位置连边,跑一遍费用流即可。
#include<bits/stdc++.h> #define int long long using namespace std; template<typename T> inline void read(T &x){ T f=1;x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} x*=f; } const int N = 5e5,INF = 2e9; int n,m,s,t,nex[N],first[N],v[N],flow[N],cost[N],num=1,a[N]; inline void add(int from,int to,int ff,int cos){ nex[++num]=first[from]; first[from]=num; v[num]=to; flow[num]=ff; cost[num]=cos; } queue<int>q; int dis[N],inf[N],pre[N],last[N],vis[N],mxflow,mincost; bool spfa(int s,int t){ memset(dis,0x7f,sizeof(dis)); memset(vis,0,sizeof(vis)); memset(inf,0x7f,sizeof(inf)); q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=first[u];i;i=nex[i]){ int to=v[i]; if(flow[i] && dis[to]>dis[u]+cost[i]){ dis[to]=dis[u]+cost[i]; pre[to]=u; last[to]=i; inf[to]=min(inf[u],flow[i]); if(!vis[to]){ vis[to]=1; q.push(to); } } } } return pre[t]!=-1; } void EK(int s,int t){ while(spfa(s,t)){ int now=t; mxflow+=inf[t]; mincost+=inf[t]*dis[t]; while(now!=s){ flow[last[now]]-=inf[t]; flow[last[now]^1]+=inf[t]; now=pre[now]; } } } signed main(){ int sum=0; read(n); s=0; t=9000; for(int i=1;i<=n;i++){ read(a[i]); sum+=a[i]; if(i==n){ add(i,i-1,INF,1); add(i-1,i,0,-1); add(n,1,INF,1); add(1,n,0,-1); } if(i==1){ add(i,i+1,INF,1); add(i+1,i,0,-1); add(1,n,INF,1); add(n,1,0,-1); } if(i!=1&&i!=n){ add(i,i+1,INF,1); add(i+1,i,0,-1); add(i,i-1,INF,1); add(i-1,i,0,-1); } } sum/=n; for(int i=1;i<=n;i++){ if(a[i]<sum){ add(i,t,sum-a[i],0); add(t,i,0,0); } if(a[i]>sum){ add(s,i,a[i]-sum,0); add(i,s,0,0); } } EK(s,t); cout<<mincost; return 0; }
4.最小路径覆盖问题:
题目链接:there
最小路径覆盖问题:
这里探讨最小不相交路径覆盖问题。
如果有这么一张图:1->2,2->4,1->3,3->4
那么里面的的最小路径,你看出来应该会是1->2->4和3->4
因为说了是最小不相交路径覆盖。
考虑最小不相交路径覆盖的定义:即两条路径经过点集的交集为空集。
于是,对于这种路径就会有一个限制:任意一个点的入度和出度均不大于1
然后,首先你会选出一些边出来保证所有的点都被经过,现在假设有x条路径,如果你发现你在加上一条路径满足这个限制,那么这两条路径就会被合并成一条,然后然后得到的路径数量就会减1
那么这里就会有一种想法:
初始的时候一条边也不加,那么这个时候的路径数量就为节点数量,然后在满足情况的条件下,往里面加的边越多,那么你的路径数就会越少,然后你就可以靠这个思路匹配到不行为止,这样留下的就回是最小路径数。
那么这里有一个神神奇奇的公式:
最小路径覆盖数=点数-二分图最大匹配数
下面有个神神奇奇的证明:
首先,考虑最常用的拆点思想,将每个点x拆分为入点x1,和出点x2。若有x->y存在边,那么x1与y2见连一条无向边,然后求最大匹配数
首先若最大匹配数为0,则二分图内无边,也就是有向图中不存在一条边,那么此时最小路径覆盖数=点数-最大匹配数=点数
若增加一条边x1->y2,那么最大匹配数加1,而此时在有向图中,x,y也在同一条路径上,那么最小路径覆盖数也就减1。
同理当继续往二分图内加边时,加到最后,你就会得到这个定理:最小路径覆盖数=点数-二分图最大匹配数
于是这道题就成了一个板子,但最坑人的是它要输出路径,这个怎么办呢?你可以就在Dinic的内部存下它会去到哪些点,在你做完二分图匹配后,从t开始遍历,如果反向边流量为1,那么即就可以往上走,然后就会输出路径。另一种想法是,你在最后可以进行一遍DFS,搜索出所有的路径并输出。具体看代码,这个地方很神奇,调了一下午才调出来,然后checker很神奇,最后一行不能打任何空行或空格,不然爆零
我放一个代码就逃了:
#include<bits/stdc++.h> #define int long long using namespace std; template<typename T> inline void read(T &x){ T f=1;x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} x*=f; } const int N = 4e6, INF = INT_MAX; int dep[N],first[N],v[N],flow[N],nex[N],q[N],no[N],aim,s,t; int num=1,vis[N],nxt[N]; void add(int from,int to,int val){ nex[++num]=first[from]; first[from]=num; v[num]=to; flow[num]=val; } bool bfs(int s,int t){ memset(dep,0,sizeof(dep)); dep[s]=1; no[s]=first[s]; q[1]=s; int head=0,tail=1; while(head!=tail){ int u=q[++head]; for(int i=first[u];i;i=nex[i]){ int to=v[i]; if(flow[i] && !dep[to]){ no[to]=first[to]; dep[to]=dep[u]+1; q[++tail]=to; } } } return dep[t]!=0; } int n,m,fa[N],son[N],too[N]; int dfs(int now,int fl){ if(now==t) return fl; int f=0; for(int i=no[now];i&&fl;i=nex[i]){ no[now]=i; int to=v[i]; if(flow[i] && dep[to]==dep[now]+1){ int x=dfs(to,min(fl,flow[i])); flow[i]-=x; flow[i^1]+=x; fl-=x; f+=x; if(x){ nxt[now]=to-n; } } } if(!f) dep[now]=-2; return f; } int mxflow(int s,int t){ int ans=0;aim=t; while(bfs(s,t)){ ans+=dfs(s,1<<30); } return ans; } signed main(){ read(n),read(m); s=0; t=8001; for(int i=1;i<=m;i++){ int x,y; read(x),read(y); add(x,y+n,1); add(y+n,x,0); } for(int i=1;i<=n;i++){ add(s,i,1); add(i,s,0); add(i+n,t,1); add(t,i+n,0); } int ans=n-mxflow(s,t); for(int x=first[t];x;x=nex[x]){ if(flow[x^1]){ int p=v[x]-n; while(p){ printf("%lld ",p); p=nxt[p]; } printf("\n"); } } printf("%lld",ans); return 0; }
5.[SDOI2010]星际竞速
题目链接:there
一句话题意:
这道题仍然考虑拆点来做。对于每个点仅经过一次的限制采用拆点限流的方法。每次瞬移后的行动可以看做一条路径。从 s向每个 u 连费用为瞬移费用的弧,从每个节点 u 向 t连费用为 0 的边。然后根据原图来建路径,因为每个点只经过自己一次,所以s和t所连边边权设为1,然后跑EK,完事 。
#include<bits/stdc++.h> #define int long long using namespace std; template<typename T> inline void read(T &x){ T f=1;x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} x*=f; } const int N = 5e5,INF = 2e9; int n,m,s,t,nex[N],first[N],v[N],flow[N],cost[N],num=1; inline void add(int from,int to,int ff,int cos){ nex[++num]=first[from]; first[from]=num; v[num]=to; flow[num]=ff; cost[num]=cos; } queue<int>q; int dis[N],inf[N],pre[N],last[N],vis[N],mxflow,mincost; bool spfa(int s,int t){ memset(dis,0x7f,sizeof(dis)); memset(vis,0,sizeof(vis)); memset(inf,0x7f,sizeof(inf)); q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=first[u];i;i=nex[i]){ int to=v[i]; // cout<<cost[i]<<" "; if(flow[i] && dis[to]>dis[u]+cost[i]){ dis[to]=dis[u]+cost[i]; pre[to]=u; last[to]=i; inf[to]=min(inf[u],flow[i]); if(!vis[to]){ vis[to]=1; q.push(to); } } } } // cout<<dis[s]<<" "<<dis[t]<<" "; return pre[t]!=-1; } void EK(int s,int t){ while(spfa(s,t)){ int now=t; mxflow+=inf[t]; mincost+=inf[t]*dis[t]; // cout<<inf[t]<<" "<<dis[t]<<" "; while(now!=s){ flow[last[now]]-=inf[t]; flow[last[now]^1]+=inf[t]; now=pre[now]; } } } signed main(){ read(n),read(m); s=0; t=9000; for(int i=1;i<=n;i++){ int x; read(x); add(s,i+n,1,x); add(i+n,s,0,-x); add(i+n,t,1,0); add(t,i+n,0,0); add(s,i,1,0); add(i,s,0,0); } for(int i=1;i<=m;i++){ int u,v,w; read(u),read(v),read(w); if(u>v) swap(u,v); add(u,v+n,1,w); add(v+n,u,0,-w); } EK(s,t); cout<<mincost; return 0; }
6.运输问题
题目链接:there
这道题才是最简单的,花了2分钟就把图建出来了,裸的带权二分图匹配,把仓库和商店分别看成点,s向仓库连流量为ai,费用为0的边,商店向t连流量为bi,费用为0的边,然后每个仓库向所有商店连边,流量设为无穷大,费用为c[i][j],然后跑最大费用最大流,最小费用最大流即可。不过我还是花了1个h,因为,是先读入m后读入n。。。
#include<bits/stdc++.h> #define int long long using namespace std; template<typename T> inline void read(T &x){ T f=1;x=0; char ch=getchar(); while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} x*=f; } const int N = 5e5,INF = 2e9; int n,m,s,t,nex[N],first[N],v[N],flow[N],cost[N],num=1; inline void add(int from,int to,int ff,int cos){ nex[++num]=first[from]; first[from]=num; v[num]=to; flow[num]=ff; cost[num]=cos; } queue<int>q; int dis[N],inf[N],pre[N],last[N],vis[N],mxflow,mincost; bool spfa(int s,int t){ memset(dis,0x3f,sizeof(dis)); memset(vis,0,sizeof(vis)); memset(inf,0x3f,sizeof(inf)); q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=first[u];i;i=nex[i]){ int to=v[i]; // cout<<cost[i]<<" "; if(flow[i] && dis[to]>dis[u]+cost[i]){ dis[to]=dis[u]+cost[i]; pre[to]=u; last[to]=i; inf[to]=min(inf[u],flow[i]); if(!vis[to]){ vis[to]=1; q.push(to); } } } } return pre[t]!=-1; } void EK(int s,int t){ while(spfa(s,t)){ int now=t; mincost+=inf[t]*dis[t]; // cout<<"here: "<<inf[t]<<" "<<dis[t]<<endl; while(now!=s){ flow[last[now]]-=inf[t]; flow[last[now]^1]+=inf[t]; now=pre[now]; } } } int a[N],b[N],c[205][205]; bool spfa2(int s,int t){ memset(dis,0xcf,sizeof(dis)); memset(vis,0,sizeof(vis)); memset(inf,0x3f,sizeof(inf)); q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=first[u];i;i=nex[i]){ int to=v[i]; // cout<<cost[i]<<" "; if(flow[i] && dis[to]<dis[u]+cost[i]){ dis[to]=dis[u]+cost[i]; pre[to]=u; last[to]=i; inf[to]=min(inf[u],flow[i]); if(!vis[to]){ vis[to]=1; q.push(to); } } } } // exit(0); return pre[t]!=-1; } void EK2(int s,int t){ while(spfa2(s,t)){ int now=t; mxflow+=inf[t]; mincost+=inf[t]*dis[t]; // cout<<inf[t]<<" "<<dis[t]<<" "<<inf[t]*dis[t]<<"\n"; while(now!=s){ flow[last[now]]-=inf[t]; flow[last[now]^1]+=inf[t]; now=pre[now]; } } } signed main(){ read(m),read(n); s=0; t=90000; for(int i=1;i<=m;i++){ read(a[i]); add(s,i,a[i],0); add(i,s,0,0); } for(int i=1;i<=n;i++){ read(b[i]); add(i+m,t,b[i],0); add(t,i+m,0,0); } for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ read(c[i][j]); add(i,j+m,INF,c[i][j]); add(j+m,i,0,-c[i][j]); } } EK(s,t); cout<<mincost<<"\n"; memset(first,0,sizeof(first)); memset(v,0,sizeof(v)); memset(cost,0,sizeof(cost)); memset(flow,0,sizeof(flow)); memset(last,0,sizeof(last)); memset(pre,0,sizeof(pre)); memset(dis,0,sizeof(dis)); memset(inf,0,sizeof(inf)); memset(nex,0,sizeof(nex)); num=1; for(int i=1;i<=m;i++){ add(s,i,a[i],0); add(i,s,0,0); } for(int i=1;i<=n;i++){ add(i+m,t,b[i],0); add(t,i+m,0,0); } for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ add(i,j+m,INF,c[i][j]); add(j+m,i,0,-c[i][j]); } } mincost=mxflow=0; EK2(s,t); cout<<mincost; return 0; }

