算法题：跳房子游戏问题（爬楼梯问题进阶） 求解受限制情况下的方案数目
问题
跳房子，规定总共有n个格子，每次可以选择跳1个格子、2个格子或3个格子，但是下一步不能和当前选择的跳跃距离一样，计算总共有多少种跳房子方案。
分析
这就是经典爬楼梯问题的进阶，仅仅换了个说法，但是比经典的爬楼梯问题难了不少，传统的爬楼梯问题一次可以上1或2个台阶没有连续动作选择的限制，核心解法是可以列出一个斐波那契数列，\(f(n) = f(n-1) + f(n-2)\)，递归的2个特殊终止条件是\(f(1)=1,f(2)=2\)。
参考
上面是我参考的做法，它只限制不能连续爬2个台阶而且没有连续跨越3个台阶的选择，它给\(f(n,status)\)函数中额外添加一个参数status，表示从第n个台阶跨status个台阶（因此到达\(f(n,status)\)的前一次跨越不能跨status个台阶）。当status设置为0时是程序代码入口，表示可以从第n-1、n-2或n-3个台阶分别攀爬到第n个台阶。
Python3代码
# 求攀爬方案的总数目：
# 1. 共有n个台阶
# 2. 每次可以向上爬1、2或3个台阶
# 3. 相邻的下一次不能和本次攀爬的台阶数相同
def F(N, status):
if N < 0:
return 0
elif N == 0: # status is 1 2 or 3 没有任何限制 因为这必定是爬台阶的第一步，没有之前步骤长度的限制
return 1
elif N == 1:
if status == 1:
return 0
else: # status is 2 or 3
return 1
elif N >= 2:
if status == 0:
return F(N-1,1) + F(N-2,2) + F(N-3,3)
elif status == 1:
return F(N-2,2) + F(N-3,3)
elif status == 2:
return F(N-1,1) + F(N-3,3)
elif status == 3:
return F(N-1,1) + F(N-2,2)
if __name__ == '__main__':
n = 5
print(f"When n = {n},F numbers: {F(n, 0)}")
执行效果：
验证上述结果
代码以\(n=5\)个台阶为例做测试，爬楼方案和算法伪代码如下图所示
千万要注意递归算法的边界条件：n为负数、0或1的时候。
- 若n为负数，是不合理的，例如\(f(-1,status=3)\)渴望从-1一次爬3个台阶到2，是无解的，因此\(f(n<0,status)=0\)。
- 若n为0，无论\(status\)值为1、2或3，值都为1；这正是爬楼者在起点最初始的选择，选择不受历史的限制（因为这就是最最最开头，没有历史）。
- 若n为1，注意\(f(1,1)\)不合理，值为0，因为0=>1=>2是连续爬1个楼梯的不满足规则；\(f(1,2)=f(1,3)\)都是合理的，值为1，分别代表了0=>1=>3和0=>1=>4的爬楼梯顺序。
优化
目前没去尝试寻找是否有leetcode中收录此题目，之前的代码依赖于反复的函数迭代，f(n)通常会执行多次带来较大时间开销，这里提出一种更快的改进算法，以存储空间开销换来节省函数反复递归的时间成本。代码如下：
def F2(N):
L = [[0]*3] * N # 以数组存储空间 换 函数递归的时间 全初始化为 0
L[0] = [1,1,1] # F(0,status=1) = 1 \ F(0,status=2) = 1 \ F(0,status=2) = 1
L[1] = [0,1,1] # F(1,status=1) = 0 \ F(1,status=2) = 1 \ F(1,status=2) = 1
for n in range(2, N): # n = 2 时，F(n-3,status=3) 即 F(-1,3) 应该是0，巧合的是L[-1]即L[N-1]此时刚好是[0,0,0]
L[n] = [L[n-2][1]+L[n-3][2], L[n-1][0]+L[n-3][2], L[n-1][0]+L[n-2][1]]
return L[N-1][0] + L[N-2][1] + L[N-3][2] # 返回F(N-1,status=1) + F(N-2,status=2) + F(N-3,status=3)
if __name__ == '__main__':
n = 5
print(f"When n = {n},F numbers: {F(n, 0)}")
print(f"When n = {n},F numbers: {F2(n)}")
执行结果如下：
这里不再有函数递归的结构，而是函数从n=2开始循环一直到n=N-1。
执行时间对比
为了验证两份代码的效率，我这里设置爬楼梯台阶数N为50，执行如下时间测试代码：
import time
if __name__ == '__main__':
n = 50
ct1 = time.time()
print(f"When n = {n},F numbers: {F(n, 0)}")
ct2 = time.time()
print(f"When n = {n},F2 numbers: {F2(n)}")
ct3 = time.time()
print("Use time:")
print(ct2-ct1)
print(ct3-ct2)
结果如下：
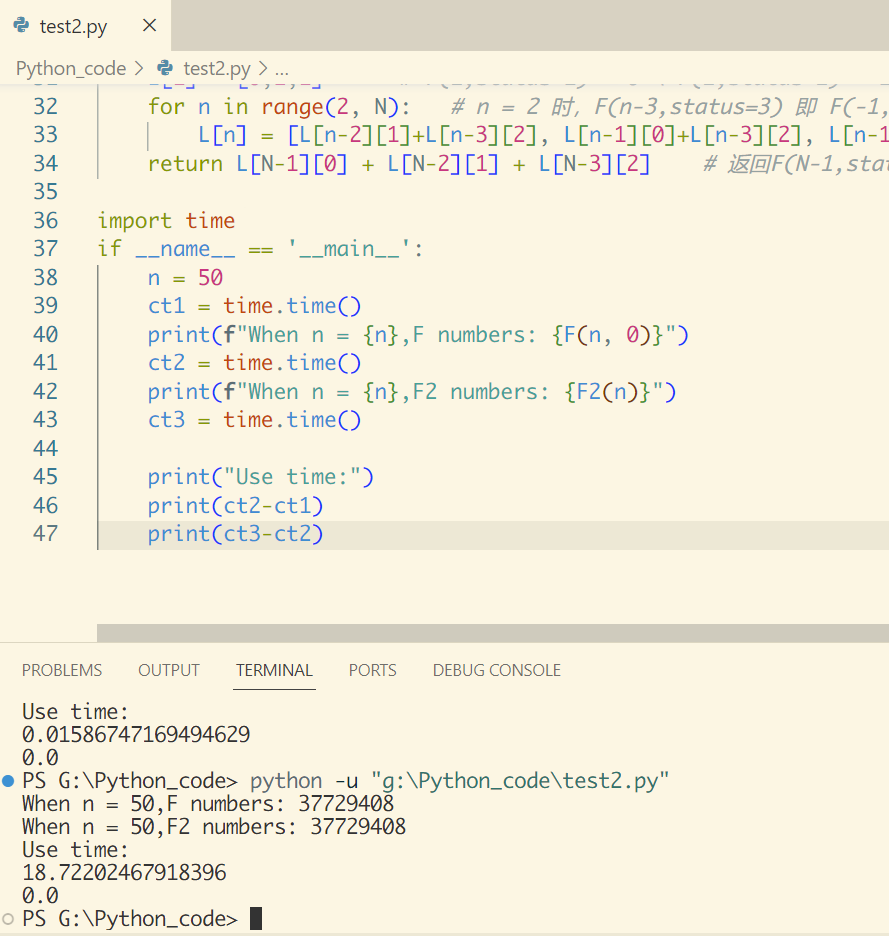
这个时间差距就已经很大了，因此在掌握第一个函数原理后，修正为无函数迭代版本的代码2更具执行时间的优势。
