常见数组的排序算法的特点

假设这些排序算法想得到一个升序序列，长度为n。

参考

https://blog.csdn.net/qq_53414724/article/details/125016223
https://zhuanlan.zhihu.com/p/602971700
https://visualgo.net/zh/sorting

冒泡排序

冒泡排序从头开始寻找相邻的元素，找到较大的元素放于后面，一直到数组末尾。循环n-1轮，每一轮都从0开始，但结束位置越来越靠近起始位置，第一轮明确最大的元素，第二轮明确第二大的元素，...。代码中i、j指针总是挨着的，满足j=i+1。冒泡排序算法稳定，平均、最差时间复杂度都是O(n^2)，最优时间复杂度为O(n)，空间复杂度为O(1)。

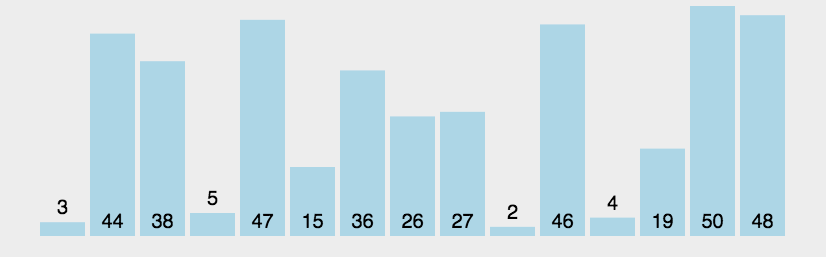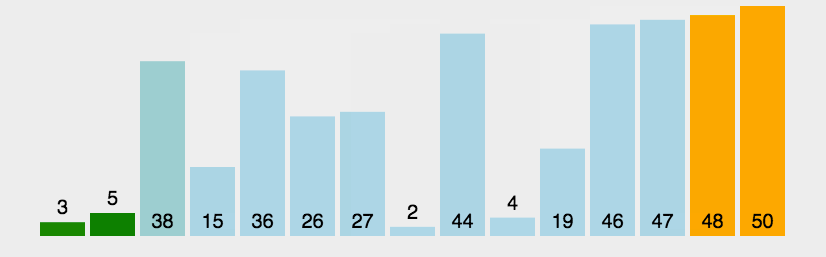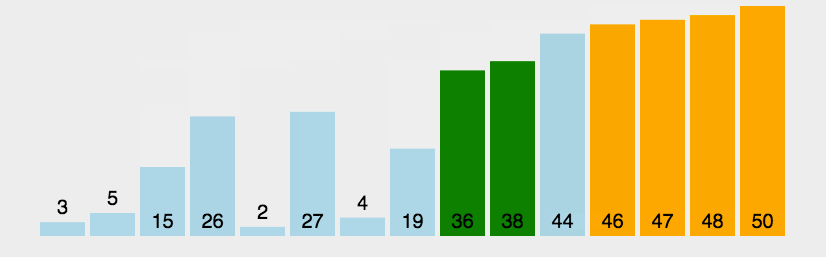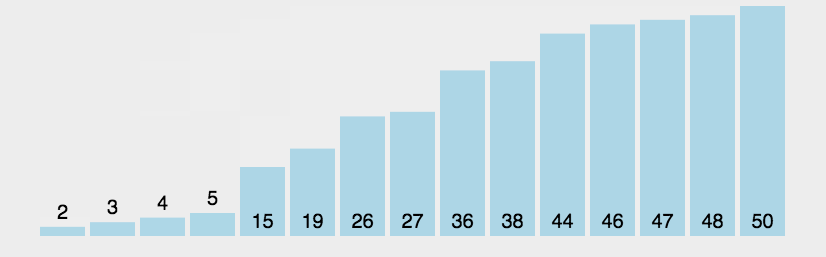
选择排序

将数组分为两部分：有序部分和无序部分。每次从无序部分中选取最小的元素，然后将其放入有序部分中，初始默认Arr[0]为有序部分，Arr[1]~Arr[n-1]皆是无序部分。共循环n-1轮，每一轮明确无序部分中最小的元素、与无序部分的第一个位置元素交换。代码中i、j指针不是挨着的，i指针指向数组无序部分的第一个位置元素，j指针遍历整个无序部分，如果碰到arr[j] < arr[i]，就立刻进行数值交换，因此每一轮中可能i、j指针指向的值交换多次。选择排序算法不稳定，平均、最好、最差时间复杂度都是O(n^2)，空间复杂度为O(1)。

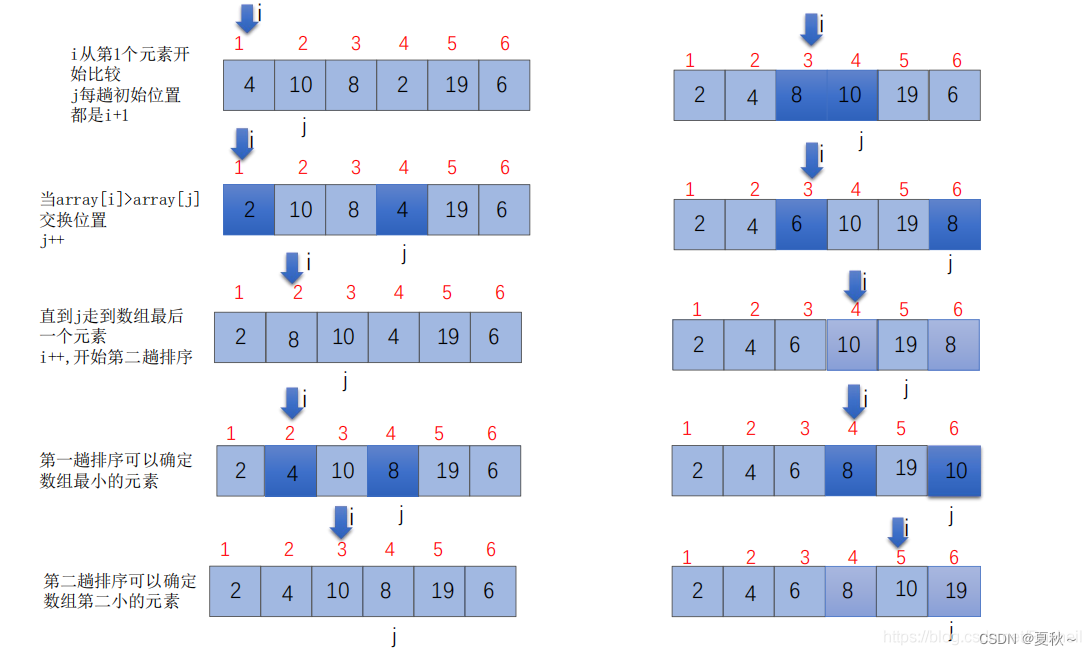
选择排序2

选择排序还有一种实现途径，原理十分相似。它同样循环n-1轮，但是每一轮中只进行一次交换。j不断遍历寻找无序部分最小值，用i指针动态指向最小值位置，当前轮结束后，对Arr[i]与Arr无序部分的第一个位置元素交换。

插入排序

思路也是将数组分为有序部分和无序部分，初始默认Arr[0]为有序部分，Arr[1]_{Arr[n-1]皆是无序部分。<b>每次将无序部分第一个元素Arr[j]插入到有序部分中的合适位置</b>，这里可能涉及到多次值对比和交换，并将Arr[j]从后往前对比大小（Arr[j-1]}Arr[1]）。插入排序算法稳定，平均、最差时间复杂度都是O(n^2)，最优时间复杂度为O(n)，空间复杂度为O(1)。在数组序列宏观大致上有序、局部乱序时效率较高，尤其是输入数组本来就有序时，只进行多次数值比较、不用进行数值交换，效率最高得到O(n)的最优时间复杂度。

希尔排序

利用了多次插入排序，目的是在数组元素很多时，缩短插入排序的时间（插入排序平均时间复杂度O(n^2)）。首先选择一个增量递减序列\(d_1\)、\(d_2\)、…、\(d_k\)，其中\(d_i\)一直递减，直到\(d_k = 1\)，则要进行k次希尔排序，先粗略排序，然后原来越精细排序，一般\(d_{i+1}=\frac{d_{i}}{2}\)向下取整。每一次排序中，数组被分为\(d_i\)个子序列，每个子序列中每组相邻元素都间隔\(d_i\)。如下图：

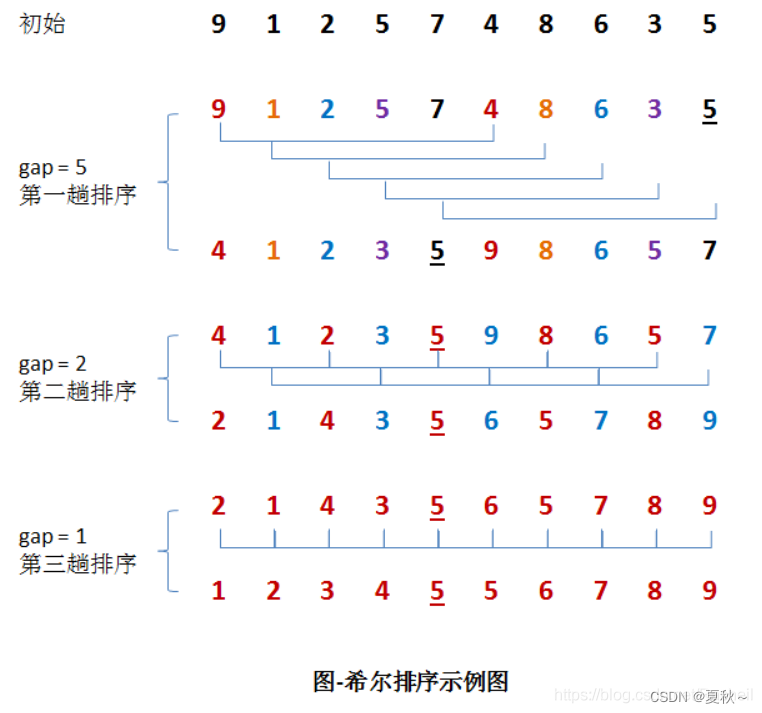
希尔排序算法不稳定，平均时间复杂度为\(O(nlogn)\)，最好时间复杂度为\(O(n^{1.3})\)，最坏时间复杂度为\(O(n^2)\)，空间复杂度为\(O(1)\)。

归并排序

把待排序列递归的分为长度相等的两个子序列，直到分解为1个子序列中包含1个元素为止。递归的将每两个子序列合并为一个有序子序列。最终合并的序列即为有序序列。归并排序算法稳定，平均时间复杂度为O(nlogn)，最好时间复杂度为O(nlogn)，最坏时间复杂度为O(nlogn)，空间复杂度为O(n)。

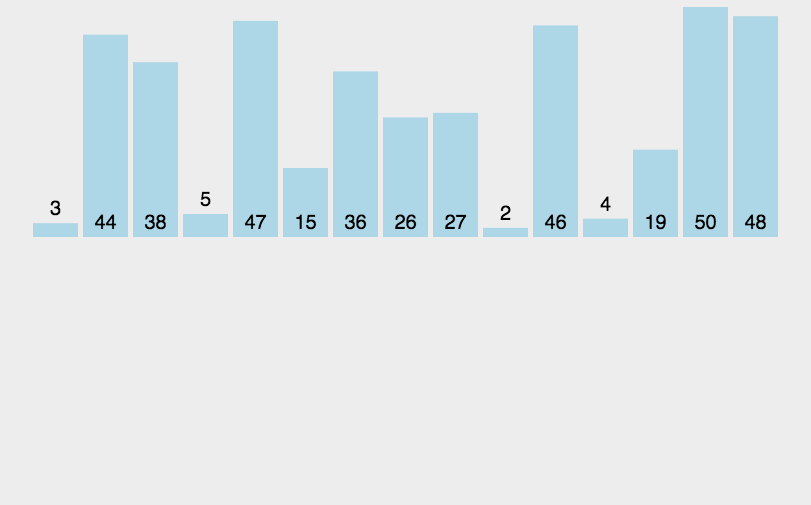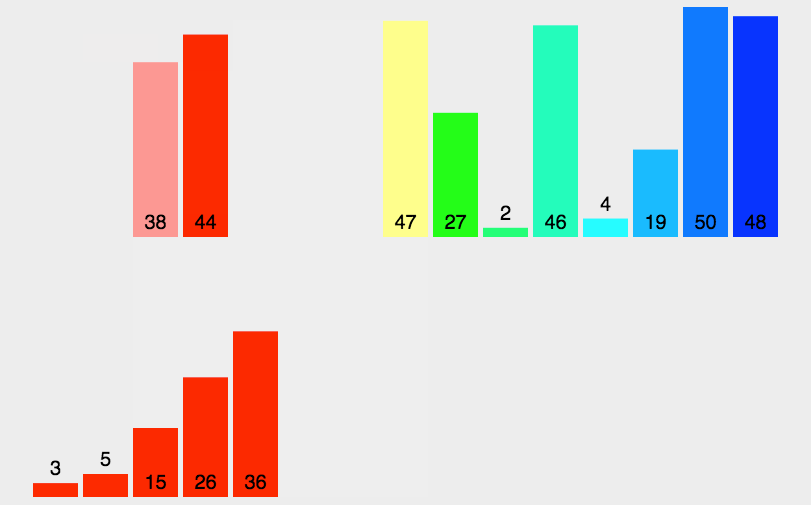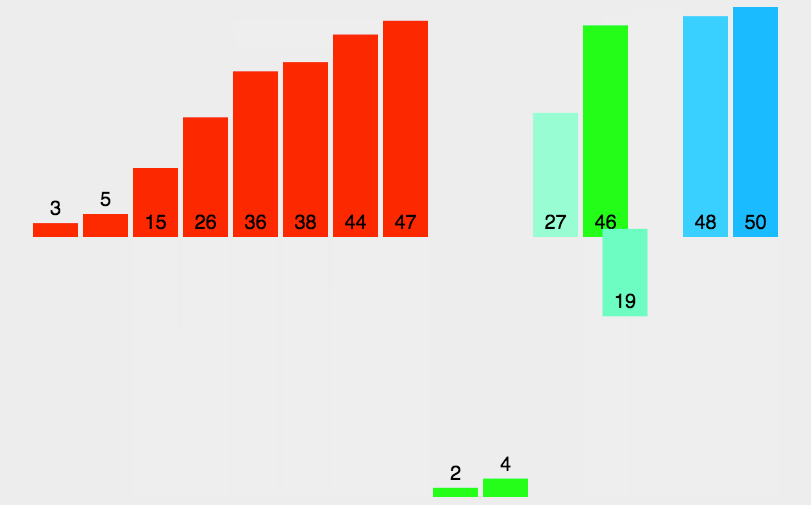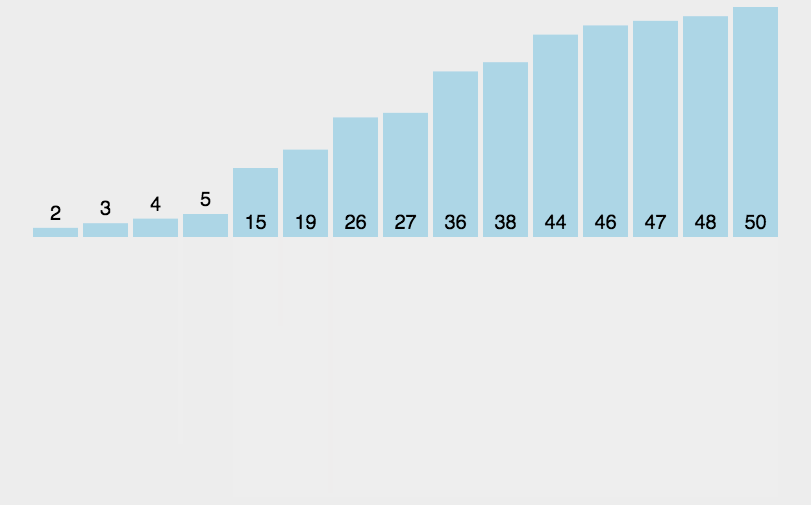
快速排序

从数列中挑出一个元素，称为"基准"（pivot）。重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。快速排序算法稳定，平均时间复杂度为O(nlogn)，最好时间复杂度为O(nlogn)，最坏时间复杂度为O(n^2)，空间复杂度为O(logn)~O(n)。

• 最好时间复杂度：当每次划分时，算法若都能分成两个等长的子序列时，分治算法效率达到最大
• 最坏时间复杂度：待排序列有序时，相当于冒泡排序，递归实现会出现栈溢出的现象，时间复杂度为O(N^2)
• 最好空间复杂度：每次都把待排序列分为相等的两部分，2^x=n (分割x次,保存x个par) ，x = logn
• 最坏空间复杂度：1 2 3 4 5 6 7 N个数据就保存N个par。