快速排序算法原理与python实现
快速排序是一种不稳定的排序算法，时间复杂度O(nlogn)，最差情况下时间复杂度为O(n^2)。
原理是：
- 选定待排序数组的任意元素为基准轴：pivot，通常选择数组第一个元素，保存下pivot数值。
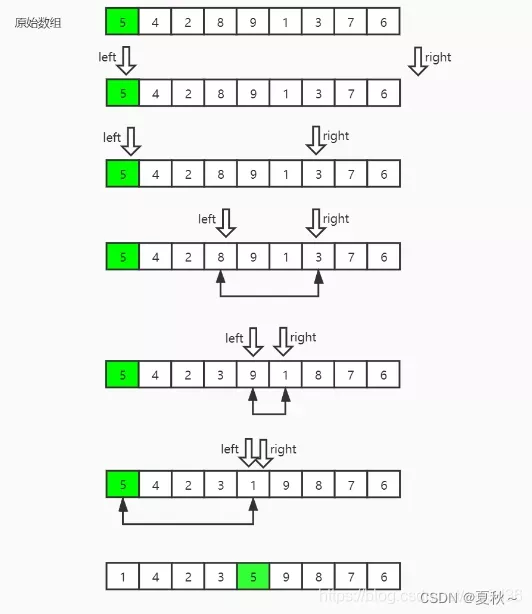
- 遍历数组中的其他元素，通过交换元素位置，数组被划分为两个子序列：左子序列元素值全小于等于pivot，右子序列元素值大于等于pivot，而2个子序列中间位置值设为pivot。
- 目前数组宏观上有序（左子序列 <= pivot <= 右子序列），微观上的左子序列、右子序列内部并不一定是有序的，递归地分别进行快速排序。
其中，算法递归结束条件是输入序列的长度为0或者是1，则算法返回。本文给出基于python3的两种实现方法，两者都需要动态地维护左指针、右指针。
QuickSort函数伪代码
输入： 待排序的数值数组Arr、左指针left、 右指针right
目标： 希望对数组的 [left,right] 区间内元素进行升序排序
1. pivot = left， value = Arr[pivot]，i = left， j = right
2. 判断是否Arr[j]小于value
2.1 若是，则 Arr[i] = Arr[j]，左指针i+=1(判断i == j ? 若是则进入第4步骤)，右指针位置不变，进入第3步骤
2.2 若否，则右指针持续递减直到符合(2.1)条件
3. 判断是否Arr[l]大于value
3.1 若是，则 Arr[r] = Arr[l]，右指针r-=1(判断i == j ? 若是则进入第4步骤)，左指针位置不变，进入第2步骤
3.2 若否，则左指针持续递增直到符合(3.1)条件
4. Arr[i] = value 或 Arr[j] = value
5. 递归：
if (i - 1) - left > 1:
QS(Arr， left，i-1)
if right - (i + 1) > 1:
QS(Arr, i+1, right)
6. 返回Arr
实现1
def QS(Arr, left, right):
pivot = left
val = Arr[pivot]
i, j = left, right
while True:
while Arr[j] >= val and i < j: # 默认情况，不需要排序
j -= 1
else:
if i == j:
break
Arr[i] = Arr[j]
i += 1
while Arr[i] <= val and i < j: # 默认情况，不需要排序
i += 1
else:
if i == j:
break
Arr[j] = Arr[i]
j -= 1
Arr[i] = val
if i - left > 2 :
QS(Arr, left, i - 1)
if right - i > 2 :
QS(Arr, i + 1, right)
if __name__ == '__main__':
NumArr = [5, 12, 1, 10, 9, 6, 2, 3]
QS(NumArr, 0, len(NumArr) - 1)
print(NumArr)
实现2
def QS(Arr, left, right):
if left >= right:
return
i,j = left,right
pivot = Arr[left]
while True:
while Arr[i] <= pivot:
i += 1
if i == right:
break
while Arr[j] >= pivot:
j -= 1
if j == left:
break
if i >= j:
break
Arr[i], Arr[j] = Arr[j], Arr[i]
Arr[left] = Arr[j] # 不能是 i ，必须是 j
Arr[j] = pivot # 不能是 i ，必须是 j
QS(Arr, left, j-1)
QS(Arr, j+1, right)
if __name__ == '__main__':
NumArr = [5, 12, 1, 10, 9, 6, 2, 3]
QS(NumArr, 0, len(NumArr) - 1)
print(NumArr)
上述两种实现途径的核心原理一致，然而具体的细节略有区别：
- 代码1中，每一次移动一个指针（如i）到达临界位置，立即进行元素值交换（Arr[j] = Arr[i]），再移动另一个指针（j）到达临界位置，立即进行元素值交换（Arr[i] = Arr[j]）；而代码2中，先分别找到左右指针i、j的临界位置，直接进行一次位置交换（Arr[i], Arr[j] = Arr[j], Arr[i]）。
- 代码1中，while循环的判定条件必须是i指针与j指针重合，重合位置被赋予已经保存的pivot值；而代码2中，while循环结束后一定是
Arr[i] > pivot且Arr[j] < pivot，则i=j+1（此时左指针在右指针右侧），此时然后将Arr[j]与Arr[0]值互相交换；因为：Arr[j] < pivot = Arr[0]，交换后Arr[j] = pivot仍满足j指针左侧子序列元素值都小于pivot。 - 代码1中，进入while循环时，必须先递减右指针j寻找临界条件，保证
Arr[0]即pivot的位置先被覆盖掉，再递增左指针i；而代码2中，Arr[0]即pivot元素的位置在while循环结束后才被Arr[j]修改。
原理参考
代码2原理： https://blog.csdn.net/qq_53414724/article/details/125016223
