Python实现 扩展的欧几里德算法求（模逆数）最大公约数

GCD算法原理：

扩展GCD算法原理：

代码呀：

def gcd(a, b):
	while a != 0:
		a, b = b%a, a
	return b

# calc : b^(-1) mod m
def IntModInverse(b, m, show = True):
    if gcd(m,b) != 1:
        return None
    A1, A2, A3 = 1, 0, m
    B1, B2, B3 = 0, 1, b
    if show:
        print('-'*54)
        print("|{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}|".format("Q","A1","A2","A3","B1","B2","B3"))
        print("|{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}|".format("-", A1, A2, A3, B1, B2, B3))
    while True:
        Q = A3//B3
        B1,B2,B3,A1,A2,A3 = (A1-Q*B1),(A2-Q*B2),(A3-Q*B3),B1,B2,B3
        if show:
            print("|{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}\t{:^5}|".format(Q, A1, A2, A3, B1, B2, B3))
        if B3 == 0:
            return None
        elif B3 == 1:
            break
    if show:
        print("-"*54)
    return B2%m

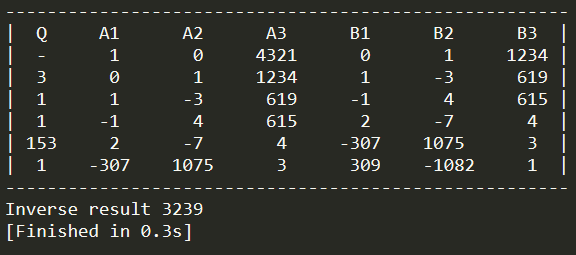
print("Inverse result", IntModInverse(1234,4321))

输出结果：