百万富翁问题的介绍与实现
参考自
- https://zhuanlan.zhihu.com/p/65564614
- https://www.jianshu.com/p/5a220e95cee2
- YAO A C.Protocols for secure computation[C].In Proc. of the 23rd Annual Symposium on Foundations of Computer Science,1982.
4.《联邦学习》杨强 刘洋等
安全多方计算
安全多方计算最初是针对一个安全两方计算问题,即所谓的“百万富翁问题”而被提出的,并与1982年被姚期智提出和推广。在安全多方计算中,目的是协同地从每一方的隐私输入中计算函数的结果,而不用将这些输入展示给其他方。
通常情况下,安全多方计算能够通过三种不同的框架来实现:不经意间传输(Oblivious Transfer,OT)、秘密共享(Secret Share,SS)和阈值同态加密(Threshold Homomorphic Encryption,THE).从某种程度上来讲,不经意传输协议和阈值同态加密方法都是用了秘密共享的思想,这可能就是为什么秘密共享被广泛认为是安全多方计算的核心。
百万富翁问题
两个富翁,分别为Alice和Bob。他们自己都清楚自己有几百万财产,也即,他们心里清楚 1~10中的一个数(代表自己百万级的财富);他们想知道到底谁的数更大一些。
这里假定:
· 两人都值得信任,不会作假
· 两人都希望诚实地比较出谁更服务(即谁的数更大)
· 两人又都希望知道对方财产到底是多少,如果可能的话,拿到具体数字最好了
· 其实这里假定的是一个安全多方计算的模型 - 半诚实对手模型,即计算方存在获取其他计算方原始数据的需求,但仍然按照计算协议执行。另外有恶意敌手模型,在这种模型中,参与方可以造假,即不按照计算协议执行计算过程。这就要复杂很多。为简化期间,本文仅讨论半诚实对手模型。
不经意传输的解决方案
一个简单的解决方案就是一下步骤:
- Alice找10个一模一样的箱子,按照1~10的顺序摆好,并按照自己的财富值分别往里面放入苹果梨和香蕉,具体放法为:如果序号小于自己的财富之,放入苹果,相等,则放入梨,大于自己的财富值,放入香蕉;把10个盒子都叫上锁;
- 并叫Bob过来(或者寄给Bob)Bob根据自己的财富值对相应的箱子再加一把锁。然后把其他所有箱子销毁。并把这个选择的箱子送给Alice。
- Alice看到送回来的箱子,但他不知道Bob选择的是第几个箱子,因为每个箱子都是一样的。
- Alice、Bob分别开锁,看里面是什么水果:
· 如果是苹果,Alice比Bob富有;
· 如果是梨,两人一样有钱
· 如果是香蕉,Bob比Alice富有
简单吧,可行吗?当然可行!前提是双方都是可信的,双方会遵守协议,所以这是一个半诚实对手模型。如果有一方造假,那么结果就不可信了。那是恶意敌手模型要讨论的问题。
密码学的解决方案

编程实现一下!
参考的知乎上君莫惘用户的代码(程序使用的是RSA公钥加密算法),进行了部分修改,主要是随机数x和p的选取要符合规范,并且满足p<x,x<N (N是RSA中的大质数,N=p*q)。
#coding=utf-8
import math
import random
# 百万富翁问题实现
# 自己生成公钥私钥并解密加密
# 算法无安全性
# 获取小于等于指定数的素数数组
def get_prime_arr(max):
prime_array = []
for i in range(2, max):
if is_prime(i):
prime_array.append(i)
return prime_array
# 判断是否为素数
def is_prime(num):
if num == 1:
raise Exception('1既不是素数也不是合数')
for i in range(2, math.floor(math.sqrt(num)) + 1):
if num % i == 0:
# print("当前数%s为非素数,其有因子%s" % (str(num), str(i)))
return False
return True
# 找出一个指定范围内与n互质的整数e
def find_pub_key(n, max_num):
while True:
# 这里是随机获取保证随机性
e = random.randint(1, max_num)
if gcd(e, n) == 1:
break
return e
# 求两个数的最大公约数
def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
# 根据e*d mod s = 1,找出d
def find_pri_key(e, s):
for d in range(100000000): # 随机太难找,就按顺序找到d,range里的数字随意
x = (e * d) % s
if x == 1:
return d
# 生成公钥和私钥
def build_key():
prime_arr = get_prime_arr(100)
p = random.choice(prime_arr)
# 保证p和q不为同一个数
while True:
q = random.choice(prime_arr)
if p != q:
break
print("随机生成两个素数p和q. p=", p, " q=", q)
n = p * q
s = (p - 1) * (q - 1)
e = find_pub_key(s, 100)
print("根据e和(p-1)*(q-1)互质得到: e=", e)
d = find_pri_key(e, s)
print("根据 e*d 模 (p-1)*(q-1) 等于 1 得到 d=", d)
print("公钥: n=", n, " e=", e)
print("私钥: n=", n, " d=", d)
return n, e, d
# 加密
def rsa_encrypt(content, ned):
# 密文B = 明文A的e次方 模 n, ned为公钥
# content就是明文A,ned【1】是e, ned【0】是n
B = pow(content, ned[1]) % ned[0]
return B
# 解密
def rsa_decrypt(encrypt_result, ned):
# 明文C = 密文B的d次方 模 n, ned为私钥匙
# encrypt_result就是密文, ned【1】是d, ned【0】是n
C = pow(encrypt_result, ned[1]) % ned[0]
return C
if __name__ == '__main__':
pbvk = build_key()
pbk = (pbvk[0], pbvk[1]) # 公钥 (n,e)
pvk = (pbvk[0], pbvk[2]) # 私钥 (n,d)
# 生成两个亿万富翁
i = random.randint(1, 10)
j = random.randint(1, 10)
print("==============================================")
print("Alice有i = %s亿,Bob有j = %s亿" % (i, j))
x = random.randint(50, pbk[0]-1) # assert(x < N) | N=p*q
print("随机选取的大整数x: %s" % x)
K = rsa_encrypt(x, pbk)
print("大整数加密后得密文K: %s" % K)
c = K - j
print("Alice收到数字c: %s" % c)
c_list = []
for k in range(1, 11):
t = rsa_decrypt(c + k, pvk)
c_list.append(t)
print("对c+1到c+10进行解密: %s" % c_list)
# 选取合适大小的p,这里根据感觉写了100以内的随机数,生成的序列的值也要求小于100
# 这个p是该算法的精华,在实际中选取p的策略要考虑到安全性和性能的因素
d_list = []
p = random.randint(30, x) # assert(p<x)
for k in range(0, 10):
d_list.append(c_list[k] % p)
print("p的值为: %s" % p)
print("除以p后的余数为: %s" % d_list)
d_list[i-1] += 1
for k in range(i, 10):
d_list[k] += 2
print("前i-1位数字不动,第i位数字+1,后面数字+2后: %s" % d_list)
print("第j个数字为: %s" % d_list[j - 1])
print("x mod p为: %s" % (x % p))
if d_list[j - 1] == x % p:
print("i>j,即Alice比Bob有钱。")
if i - j >= 0:
print("验证成功")
else:
print("代码存在错误")
elif d_list[j - 1] == (x%p)+1:
print("i=j,即Alice和Bob一样有钱。")
else:
print("i<j,即Bob比Alice有钱")
if i - j < 0:
print("验证成功")
else:
print("代码存在错误")
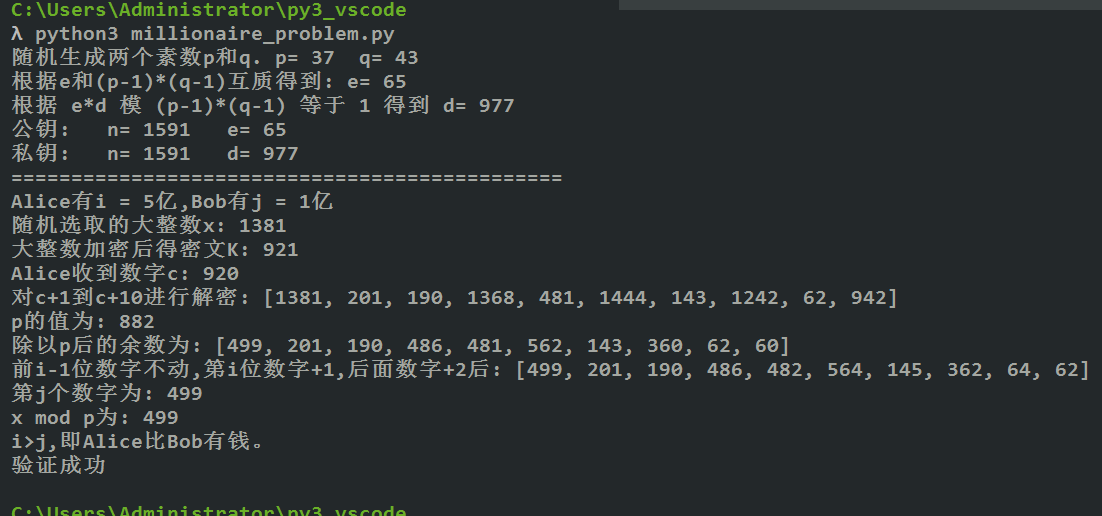
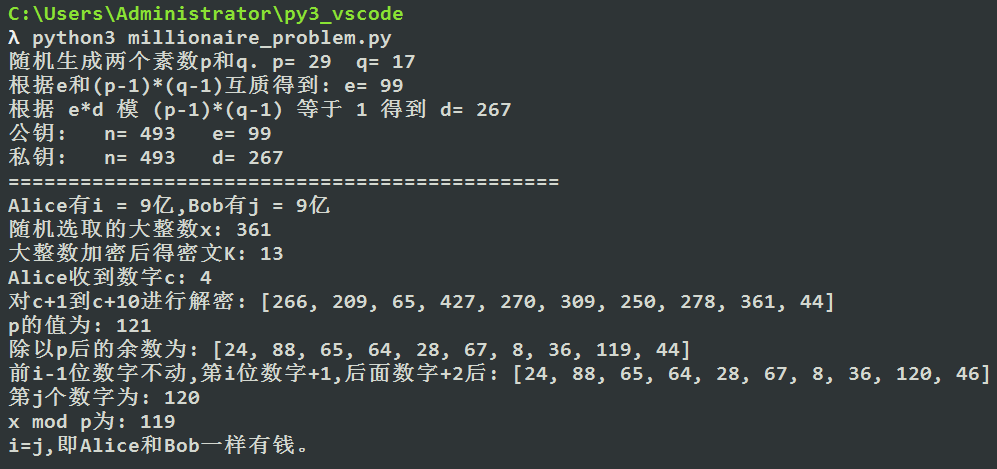
执行效果:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号