对DSA签名算法的攻击
DSA算法介绍:
DSA是在ElGamal和Schnorr两个签名方案的基础上设计的,其安全性基于求离散对数的困难性。生成签名长度 320 bit,算法描述如下:
(1) 全局公开钥
l p:满足2L-1<p<2L 的大素数,其中512≤L≤1024且L是64的倍数
l q:p-1的素因子,满足2159<q<2160 ,即q长为160比特。
l g:g=h(p-1)/q mod p,h是满足1<h<p-1且使得h(p-1)/q mod p >1的任一整数
(2) 用户秘密钥x
l x是满足0<x<q的随机数或伪随机数
(3) 用户的公开钥y
l y≡gx mod p。
(4) 用户为待签消息选取的秘密数k
l k是满足0<k<q的随机数或伪随机数。
(5) 签名过程
l 用户对消息M的签名为(r, s),其中r≡(gk mod p) mod q
l s≡[k-1(H(M)+xr)] mod q,H(M)是由SHA求出的杂凑值
(6) 验证过程
l 设接收方收到的消息为M¢,签名为(r¢,s¢)。计算
l w≡(s¢)-1 mod q,u1≡[H(M¢)w] mod q
l u2≡r¢w mod q, v≡[(gu1yu2) mod p] mod q
l 检查v=r ¢是否成立,若相等,则认为签名有效。
1.利用如下的参数,恢复DSA的秘密钥x。
1 p = 800000000000000089e1855218a0e7dac38136ffafa72eda7859f2171e25e65eac698c1702578b07dc2a1076da241c76c62d374d8389ea5aeffd3226a0530cc565f3bf6b50929139ebeac04f48c3c84afb796d61e5a4f9a8fda812ab59494232c7d2b4deb50aa18ee9e132bfa85ac4374d7f9091abc3d015efc871a584471bb1 2 q = f4f47f05794b256174bba6e9b396a7707e563c5b 3 g = 5958c9d3898b224b12672c0b98e06c60df923cb8bc999d119458fef538b8fa4046c8db53039db620c094c9fa077ef389b5322a559946a71903f990f1f7e0e025e2d7f7cf494aff1a0470f5b64c36b625a097f1651fe775323556fe00b3608c887892878480e99041be601a62166ca6894bdd41a7054ec89f756ba9fc95302291 4 y = 84ad4719d044495496a3201c8ff484feb45b962e7302e56a392aee4abab3e4bdebf2955b4736012f21a08084056b19bcd7fee56048e004e44984e2f411788efdc837a0d2e5abb7b555039fd243ac01f0fb2ed1dec568280ce678e931868d23eb095fde9d3779191b8c0299d6e07bbb283e6633451e535c45513b2d33c99ea17
被签名的消息为:So be friendly, a matter of life and death, just like a etch-a-sketch,它的SHA1 值为(十六进制):0xd2d0714f014a9784047eaeccf956520045c45265。
得到的签名为:
r = 548099063082341131477253921760299949438196259240
s = 857042759984254168557880549501802188789837994940
已知签名用的"k" 的范围是 0 到2^16。
请编程恢复DSA的秘密钥x,它的SHA1 值为:0954edd5e0afe5542a4adf012611a91912a3ec16
思路:
首先,根据题目提示,可以根据r的取值先计算求出k的值(r≡(gk mod p) mod q);因为2^16穷举一下很轻松,时间复杂度还是可以接受的。
1 #先恢复k的值,穷举1-65536 2 for k in range(2**16): 3 temp=fastExpMod(g,k,p) 4 temp %=q 5 if temp == r: 6 break 7 else: 8 pass 9 print "k=",k
上面用到了:自定义的幂次取模的函数fastExpMod,
1 def fastExpMod(b, e, m): #快速幂取模函数;b为底数,e为指数,m为模数 2 result = 1 3 while e != 0: 4 if (e&1) == 1: 5 result = (result * b) % m 6 e >>= 1 7 b = (b*b) % m 8 return result #返回取模结果
其次,可以根据s的取值计算x:
从 s≡[k-1(H(M)+xr)] mod q ,可以继续推出 x≡r -1 *[ks-H(M)] mod q
这一步将要计算r -1的取值,用到一个自定义的求模逆函数:findModReverse,函数原理是基于扩展欧几里得算法求模逆,贴一下代码:
1 def gcd(a,b): #求最大公约数函数 2 while a!=0: 3 a,b = b%a,a 4 return b 5 def findModReverse(a,m):#这个扩展欧几里得算法求模逆 6 if gcd(a,m)!=1: 7 return None 8 u1,u2,u3 = 1,0,a 9 v1,v2,v3 = 0,1,m 10 while v3!=0: 11 q = u3//v3 12 v1,v2,v3,u1,u2,u3 = (u1-q*v1),(u2-q*v2),(u3-q*v3),v1,v2,v3 13 return u1%m
完整代码:
# -*- coding=utf-8 -*- # py2 import hashlib p = 0x800000000000000089e1855218a0e7dac38136ffafa72eda7859f2171e25e65eac698c1702578b07dc2a1076da241c76c62d374d8389ea5aeffd3226a0530cc565f3bf6b50929139ebeac04f48c3c84afb796d61e5a4f9a8fda812ab59494232c7d2b4deb50aa18ee9e132bfa85ac4374d7f9091abc3d015efc871a584471bb1 q = 0xf4f47f05794b256174bba6e9b396a7707e563c5b g = 0x5958c9d3898b224b12672c0b98e06c60df923cb8bc999d119458fef538b8fa4046c8db53039db620c094c9fa077ef389b5322a559946a71903f990f1f7e0e025e2d7f7cf494aff1a0470f5b64c36b625a097f1651fe775323556fe00b3608c887892878480e99041be601a62166ca6894bdd41a7054ec89f756ba9fc95302291 y = 0x84ad4719d044495496a3201c8ff484feb45b962e7302e56a392aee4abab3e4bdebf2955b4736012f21a08084056b19bcd7fee56048e004e44984e2f411788efdc837a0d2e5abb7b555039fd243ac01f0fb2ed1dec568280ce678e931868d23eb095fde9d3779191b8c0299d6e07bbb283e6633451e535c45513b2d33c99ea17 hash_x=0x0954edd5e0afe5542a4adf012611a91912a3ec16 Hash_M=0xd2d0714f014a9784047eaeccf956520045c45265 r = 548099063082341131477253921760299949438196259240 s = 857042759984254168557880549501802188789837994940 def fastExpMod(b, e, m): #快速幂取模函数;b为底数,e为指数,m为模数 result = 1 while e != 0: if (e&1) == 1: result = (result * b) % m e >>= 1 # b, b^2, b^4, b^8, ... , b^(2^n) b = (b*b) % m return result def gcd(a,b): #求最大公约数函数 while a!=0: a,b = b%a,a return b def findModReverse(a,m): #这个扩展欧几里得算法求模逆 if gcd(a,m)!=1: return None u1,u2,u3 = 1,0,a v1,v2,v3 = 0,1,m while v3!=0: q = u3//v3 v1,v2,v3,u1,u2,u3 = (u1-q*v1),(u2-q*v2),(u3-q*v3),v1,v2,v3 return u1%m if __name__ == '__main__': #先恢复k的值,穷举1-65536 for k in range(2**16): temp=fastExpMod(g,k,p) temp %=q if temp == r: break else: pass print "k=",k r_rev=findModReverse(r,q) print "r^-1=",r_rev x=(k*s-Hash_M)%q x=x*r_rev %q print "x=",x hex_x=hex(x)[2:-1] print "hex_x=",hex_x Hash_x=hashlib.sha1(hex_x).hexdigest() print "Sha1(x)=",Hash_x if hash_x==int(Hash_x,16): print "哈希匹配,求解私钥x正确!"
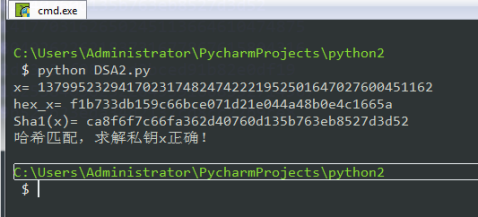
执行结果:

2.如下是十一组消息及其DSA签名:
msg: Listen for me, you better listen for me now. s: 1267396447369736888040262262183731677867615804316 r: 1105520928110492191417703162650245113664610474875 m: a4db3de27e2db3e5ef085ced2bced91b82e0df19
msg: Listen for me, you better listen for me now. s: 29097472083055673620219739525237952924429516683 r: 51241962016175933742870323080382366896234169532 m: a4db3de27e2db3e5ef085ced2bced91b82e0df19
msg: When me rockin' the microphone me rock on steady, s: 277954141006005142760672187124679727147013405915 r: 228998983350752111397582948403934722619745721541 m: 21194f72fe39a80c9c20689b8cf6ce9b0e7e52d4
msg: Yes a Daddy me Snow me are de article dan. s: 1013310051748123261520038320957902085950122277350 r: 1099349585689717635654222811555852075108857446485 m: 1d7aaaa05d2dee2f7dabdc6fa70b6ddab9c051c5
msg: But in a in an' a out de dance em s: 203941148183364719753516612269608665183595279549 r: 425320991325990345751346113277224109611205133736 m: 6bc188db6e9e6c7d796f7fdd7fa411776d7a9ff
msg: Aye say where you come from a, s: 502033987625712840101435170279955665681605114553 r: 486260321619055468276539425880393574698069264007 m: 5ff4d4e8be2f8aae8a5bfaabf7408bd7628f43c9
msg: People em say ya come from Jamaica, s: 1133410958677785175751131958546453870649059955513 r: 537050122560927032962561247064393639163940220795 m: 7d9abd18bbecdaa93650ecc4da1b9fcae911412
msg: But me born an' raised in the ghetto that I want yas to know, s: 559339368782867010304266546527989050544914568162 r: 826843595826780327326695197394862356805575316699 m: 88b9e184393408b133efef59fcef85576d69e249
msg: Pure black people mon is all I mon know. s: 1021643638653719618255840562522049391608552714967 r: 1105520928110492191417703162650245113664610474875 m: d22804c4899b522b23eda34d2137cd8cc22b9ce8
msg: Yeah me shoes a an tear up an' now me toes is a show a s: 506591325247687166499867321330657300306462367256 r: 51241962016175933742870323080382366896234169532 m: bc7ec371d951977cba10381da08fe934dea80314
msg: Where me a born in are de one Toronto, so s: 458429062067186207052865988429747640462282138703 r: 228998983350752111397582948403934722619745721541 m: d6340bfcda59b6b75b59ca634813d572de800e8f
这些消息的签名公钥为:
y = 2d026f4bf30195ede3a088da85e398ef869611d0f68f0713d51c9c1a3a26c95105d915e2d8cdf26d056b86b8a7b85519b1c23cc3ecdc6062650462e3063bd179c2a6581519f674a61f1d89a1fff27171ebc1b93d4dc57bceb7ae2430f98a6a4d83d8279ee65d71c1203d2c96d65ebbf7cce9d32971c3de5084cce04a2e147821
另外,参数p,q,g与上一题的相同。
请编程恢复DSA的秘密钥x,它的SHA1 值为:ca8f6f7c66fa362d40760d135b763eb8527d3d52
思路:
从题目所知道的,p、q、g和第一题一样不变,变的是k的值以及私钥x(显然公钥y也要随着改变)。特点是这十一组数据和签名都有共同的私钥x,但是k并不完全一样,首先寻找规律,发现存在几组数据的r值相同,根据定义 r≡(gk mod p) mod q,说明这几组的k值相同
下面图中几组是整理的r相同的几组
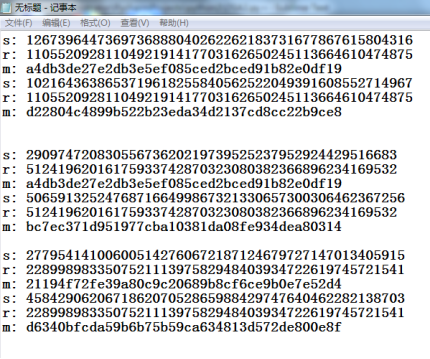
下面是计算x的推导公式,s1、s2代表的是r值相同的两组(从上图三组中任取一组),这样的好处是,虽然不知到k的取值,但是两个方程两个未知数便可以约去一个k甚至能求出k,并且得到x的取值
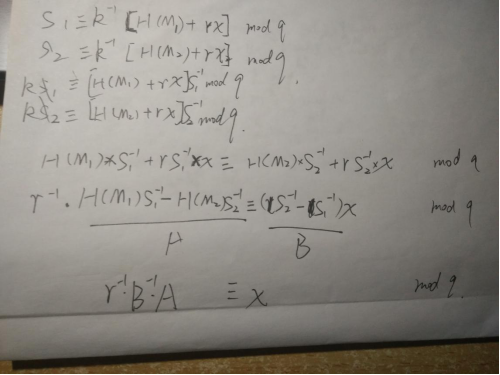
完整代码:
1 # -*- coding=utf-8 -*- 2 # py2 3 import hashlib 4 p = 0x800000000000000089e1855218a0e7dac38136ffafa72eda7859f2171e25e65eac698c1702578b07dc2a1076da241c76c62d374d8389ea5aeffd3226a0530cc565f3bf6b50929139ebeac04f48c3c84afb796d61e5a4f9a8fda812ab59494232c7d2b4deb50aa18ee9e132bfa85ac4374d7f9091abc3d015efc871a584471bb1 5 q = 0xf4f47f05794b256174bba6e9b396a7707e563c5b 6 g = 0x5958c9d3898b224b12672c0b98e06c60df923cb8bc999d119458fef538b8fa4046c8db53039db620c094c9fa077ef389b5322a559946a71903f990f1f7e0e025e2d7f7cf494aff1a0470f5b64c36b625a097f1651fe775323556fe00b3608c887892878480e99041be601a62166ca6894bdd41a7054ec89f756ba9fc95302291 7 y = 0x2d026f4bf30195ede3a088da85e398ef869611d0f68f0713d51c9c1a3a26c95105d915e2d8cdf26d056b86b8a7b85519b1c23cc3ecdc6062650462e3063bd179c2a6581519f674a61f1d89a1fff27171ebc1b93d4dc57bceb7ae2430f98a6a4d83d8279ee65d71c1203d2c96d65ebbf7cce9d32971c3de5084cce04a2e147821 8 hash_x=0xca8f6f7c66fa362d40760d135b763eb8527d3d52 9 r = 1105520928110492191417703162650245113664610474875 10 s1= 1267396447369736888040262262183731677867615804316 11 hash_m1 = 0xa4db3de27e2db3e5ef085ced2bced91b82e0df19 12 s2 = 1021643638653719618255840562522049391608552714967 13 hash_m2 = 0xd22804c4899b522b23eda34d2137cd8cc22b9ce8 14 15 def gcd(a,b): 16 while a!=0: 17 a,b = b%a,a 18 return b 19 def findModReverse(a,m): 20 if gcd(a,m)!=1: 21 return None 22 u1,u2,u3 = 1,0,a 23 v1,v2,v3 = 0,1,m 24 while v3!=0: 25 q = u3//v3 26 v1,v2,v3,u1,u2,u3 = (u1-q*v1),(u2-q*v2),(u3-q*v3),v1,v2,v3 27 return u1%m 28 s1_rev = findModReverse(s1,q) 29 s2_rev = findModReverse(s2,q) 30 r_rev = findModReverse(r,q) 31 A=(hash_m1*s1_rev-hash_m2*s2_rev) %q 32 B=(s2_rev-s1_rev) %q 33 34 B_rev=findModReverse(B,q) 35 x_tmp=(A*B_rev) %q 36 x=(x_tmp*r_rev) %q 37 # x=(A*r_rev*B_rev) %q 38 print "x=",x 39 hex_x=hex(x)[2:-1] 40 print "hex_x=",hex_x 41 Hash_x=hashlib.sha1(hex_x).hexdigest() 42 print "Sha1(x)=",Hash_x 43 if hash_x==int(Hash_x,16): 44 print "哈希匹配,求解私钥x正确!"
运行结果: