2019-ACM-ICPC-徐州站网络赛- I. query-二维偏序+树状数组

2019-ACM-ICPC-徐州站网络赛- I. query-二维偏序+树状数组

---

【Problem Description】

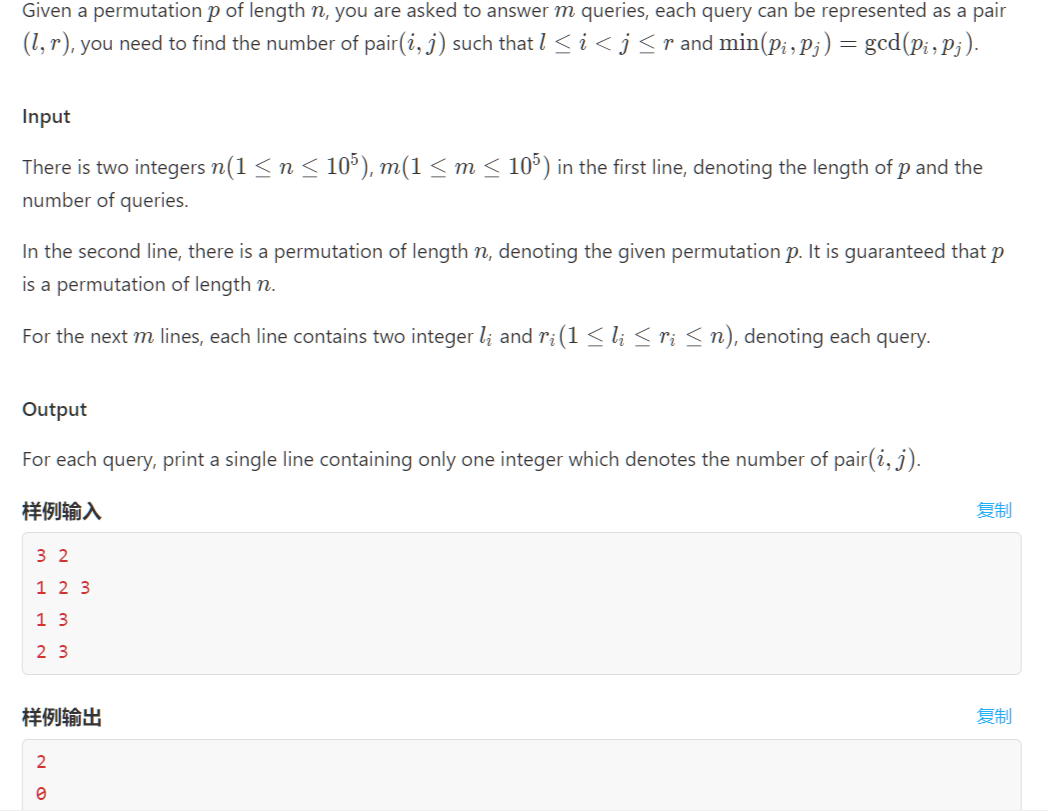
​ 给你一个\([1,n]\)的排列，查询\([l,r]\)区间内有多少对\((i,j)\)满足\(l\le i<j\le r\)，且\(min(p_i,p_j)=gcd(p_i,p_j)\)。

【Solution】

​ 将所有询问按区间右端点从小到大排序，对于排序后的每一个询问，将\([1,r]\)中所有满足条件的插入到树状数组中，然后查询区间大小即可。(\([1,r]\)中所有满足条件的的数为\([1,i)\)中\(a[i]\)的约数或倍数，其中\(i\in[1,r]\))

​ 重点在于预处理，对于排列中的每个数\(p_i\)，枚举它的倍数，找到这个数出现的位置\(pos\)，若\(pos>i\)，则\(g[pos].push\_back(i)\)，否则\(g[i].push\_back(pos)\)。即\(g[x]\)中存储的就是\([1,x)\)中\(a[x]\)的约数和倍数所在的位置。

---

【Code】

/*
 * @Author: Simon 
 * @Date: 2019-09-10 21:25:49 
 * @Last Modified by: Simon
 * @Last Modified time: 2019-09-10 22:06:20
 */
#include<bits/stdc++.h>
using namespace std;
typedef int Int;
#define int long long
#define INF 0x3f3f3f3f
#define maxn 200005
int tree[maxn],ans[maxn];
vector<int>g[maxn]; //[1,x)中a[x]的约数或倍数所在的位置
vector<pair<int,int> >q[maxn]; //右端点为r的所有查询
int pos[maxn],a[maxn];
inline int lowbit(int x){
    return x&(-x);
}
inline void update(int x,int val){
    for(int i=x;i<maxn;i+=lowbit(i)){
        tree[i]+=val;
    }
}
inline int query(int x){
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i)){
        ans+=tree[i];
    }
    return ans;
}
Int main(){
#ifndef ONLINE_JUDGE
    //freopen("input.in","r",stdin);
    //freopen("output.out","w",stdout);
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n,m;cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];pos[a[i]]=i;
    }
    for(int i=1;i<=n;i++){
        for(int j=a[i]*2;j<=n;j+=a[i]){
            int x=i,y=pos[j];
            if(x<y) swap(x,y);
            g[x].push_back(y);
        }
    }
    for(int i=1;i<=m;i++){
        int l,r;cin>>l>>r;
        q[r].push_back({l,i});//按右端点分类
    }
    for(int i=1;i<=n;i++){
        for(auto v:g[i]) update(v,1); //将小于i的满足条件的数都插入树状数组中
        for(auto v:q[i]) ans[v.second]=query(i)-query(v.first-1); //查询
    }
    for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
#ifndef ONLINE_JUDGE
    cout<<endl;system("pause");
#endif
    return 0;
}