树的重心(树形DP)
树的重心定义
对于一棵无根树,任选一个点为根节点,以根节点为分界,得到若干个子树,具有结点数最多的子树就是最大子树。以每个点为根节点,最大子树中结点数最小的那个根节点就是树的重心。(百度定义:树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心)
或者树的重心还可以定义为:去掉该结点后,树的各个连通分支中含有的结点最小。
以下图为例:
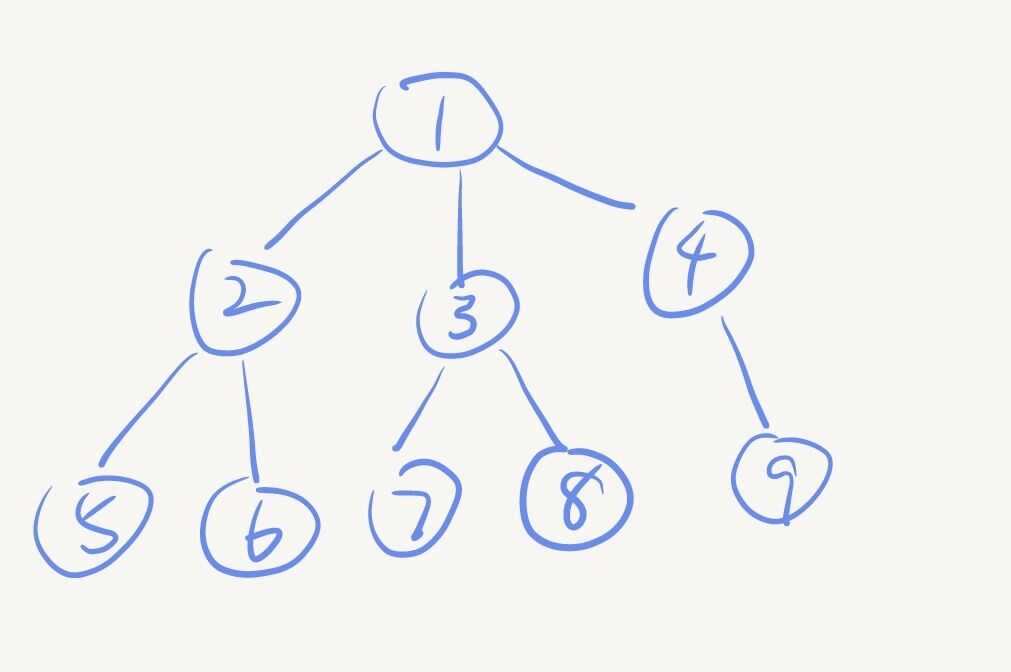
以1当作根节点,其所有子树的结点数为3,3,2。1的最大子树就是3。
1就是树的重心,因为以其他点为根节点时,最大子树的结点数都会超过3
如以2为根节点,最大子树为{1,2,4,7,8,9}
输入输出
输入:第一行一个整数n,表示树的结点个数。
接下来n-1行,每行两个数i,j。表示i和j有边相连。
输出:第一行一个整数k,表示重心的个数。
接下来K行,每行一个整数,表示重心。按从小到大的顺序给出。
思路
任选一个结点作为根节点,用DFS进行遍历,求出所有结点的子树大小(大小就是子树所含的结点数),所有结点还有一个到根节点的子树,大小为总结点数-当前结点所含所有子树的大小。求出每个结点最大子树的结点数,再求最小值。
int sz[N],mx[N]; //sz[i]是以i为根节点的子树大小,mx[i]是以i为根节点的子树的最大子树大小
void dfs(int u,int pre){
sz[u] = 1; //自己也要算进去
mx[u] = 0;
for(int i = head[u];i;i = nxt[i]){
int v = ver[i];
if(v == pre) continue;
dfs(v,u);
sz[u] += sz[v]; //dfs搜索完v之后,更新sz[u]
mx[u] = max(mx[u],sz[v]); //更新最大子树的大小
}
mx[u] = max(mx[u], n-sz[u]); //还要与到根节点那颗子树的大小比较
}
树的重心的性质
- 一棵树最少有一个重心,最多有两个重心,若有两个重心,则它们相邻(即连有直接边)。
- 树上所有点到某个点的距离和里,到重心的距离和最小;若有两个重心,则其距离和相同。
- 若以重心为根,则所有子树的大小都不超过整棵树的一半。否则可以通过平移使得最大子树的大小缩小至整树的一半,剩下子树的大小最大为 n/2−1 。此时新平移到的点才是真正的重心。
- 在一棵树上添加或删除一个叶子节点,其重心最多平移一条边的距离。
- 两棵树通过连一条边组合成新树,则新树重心在原来两棵树的重心的连线上。
解题
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int tot;
int head[N],ver[N],nxt[N]; //邻接表建树需要的数组
int sz[N],mx[N]; //sz是以i为根节点的子树的大小,mx是每个点的最大子树大小
void addedge(int u,int v){ //邻接表建树过程
tot++;
nxt[tot] = head[u];
ver[tot] = v;
head[u] = tot;
}
int n, minn = 1e8;
void dfs(int u,int pre){
sz[u] = 1; //自己也要算进去
mx[u] = 0;
for(int i = head[u];i;i = nxt[i]){
int v = ver[i];
if(v == pre) continue;
dfs(v,u);
sz[u] += sz[v]; //dfs搜索完v之后,更新sz[u]
mx[u] = max(mx[u],sz[v]); //更新最大子树的大小
}
mx[u] = max(mx[u], n-sz[u]); //还要与到根节点那颗子树的大小比较
if(mx[u] < minn) minn = mx[u];
}
int main()
{
int u,v;
cin >> n;
for(int i = 1;i <= n-1;i++){ //建立边
cin >> u >> v;
addedge(u,v);
}
dfs(1,0); //进行dfs遍历
int len=0,p[2];
for(int i = 1;i <= n;i++){ //寻找树的重心
if(mx[i] == minn)
p[len++] = i;
}
cout << len << endl; //输出
for(int i = 0;i < len;i++){
cout << p[i] << endl;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号