树的算法（学习记录）

一、二叉树的存储结构

1.顺序存储结构（适合满二叉树和完全二叉树）

#define MAX_TREE_SIZE 100	//二叉树最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE];	//0号结点存储根结点
SqBiTree bt;

2.链式存储结构
二叉链表存储

typedef struct BiTNode{
    TElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

二、二叉树的遍历

先序遍历

Status PreOrderTraverse(BiTree T,status (*Visit)(TElemType e)){
    if(T){	//树非空
        if(visit(T->data)){
           if(PreOrderTraverse(T->lchild,visit))
               if(PreOrderTraverse(T->rchild,visit))
            		return OK;
        }
    }
    else	//树为空
        return OK;
}

三、构造二叉树

先序构造

Status CreatBiTree(BiTree &T){
    scanf(&ch);	//输入一个字符
    if(ch==' ')
        T=NULL;
    else{
        if(!(T=(BiTNode*)malloc(size(BiTNode))))
            exit(OVERFLOW);
		T->data=ch;
       	//递归构造左子树、右子树
        CreatBiTree(T->lchild);
        CreatBiTree(T->rchild);
    }
    return OK;
}

由先序序列和中序序列构造二叉树
由图所示

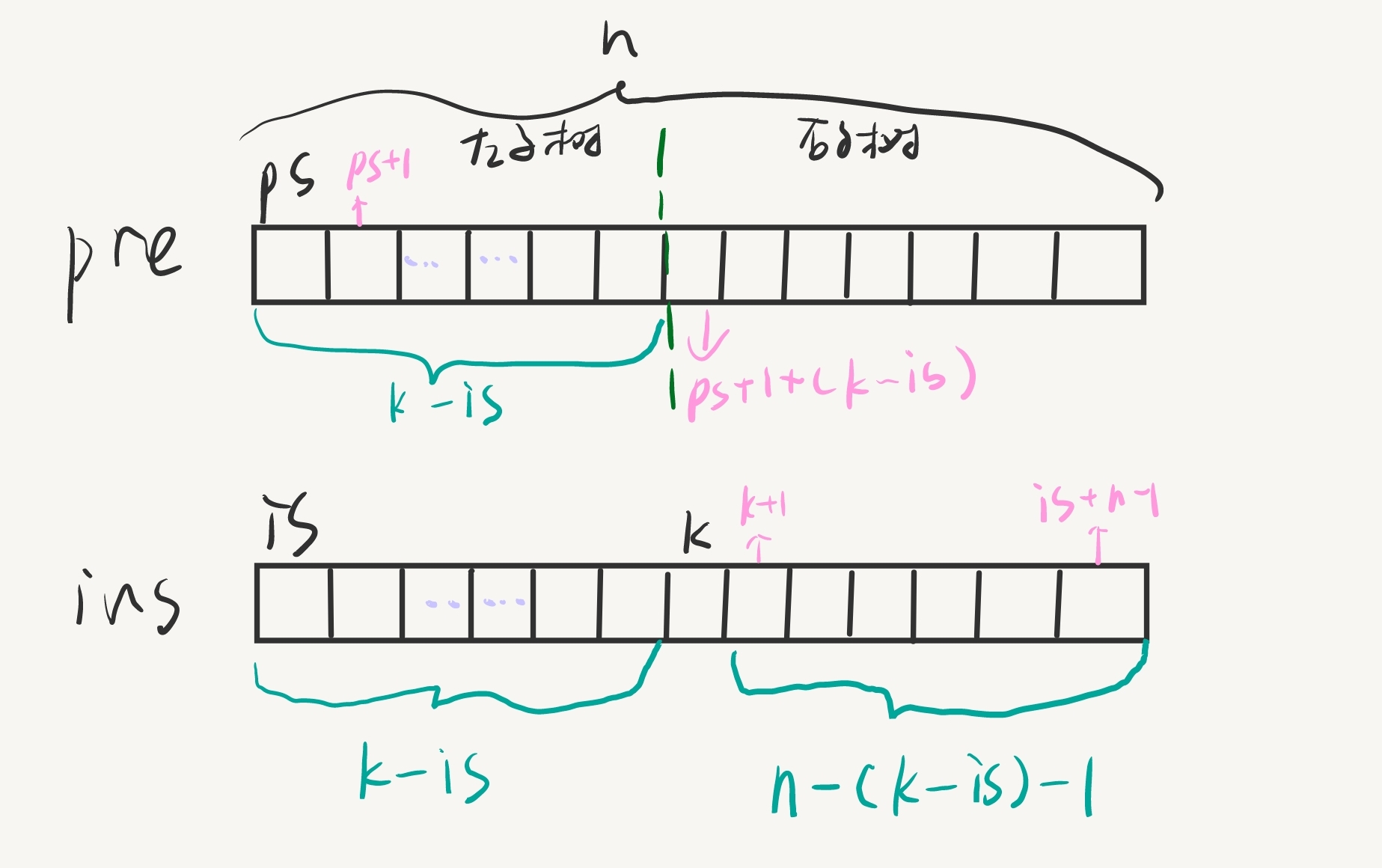
void CrtBT(BiTree &T,char pre[],char ins[],int ps,int is,int n){
    //pre[]:前序序列所在字符数组，ins[]:中序序列所在字符数组
    //ps：前序序列起点，is：中序序列起点，n为序列长度
    if(n==0)
        T=NULL;
    else{
        k=Search(ins,pre[ps]);	//k为前序序列中根结点在中序序列中的位置
        if(k==-1){	//没找到为空树
            T=NULL;
        }
        else{	//寻找到k
            if(!(T=(BiTNode*)malloc(size(BiTNode))))	//创建一个结点
            	exit(OVERFLOW);
            T->data=pre[ps];	//根结点为前序序列的第一个结点
            if(k==is)	//左子树为空
                T->lchild=NULL;
            else{	//递归创建左子树
                CrtBT(T->lchild,pre,ins,ps+1,is,k-is);
            }
            if(k==is+n-1)	//右子树为空
                T->rchild=NULL;
            else{	//递归创建右子树
                CrtBT(T->rchild,pre,ins,ps+(k-is)+1,k+1,n-(k-is)-1);
            }
        }
    }
}

四、遍历算法的应用

1.统计二叉树中叶子结点的个数（先序遍历）

void CountLeaf(BiTree T,int &count){
    if(T){	//树不为空
        if(!T->lchild && !T->rchild){	//当前为叶子结点
            count++;
        }
        else{
            CountLeaf(T->lchild,count);
            CountLeaf(T->rchild,count);
        }
    }
}

2.求二叉树的深度（后序遍历）
二叉树的深度为左子树和右子树的最大值加1
树的深度为：左子树加1和右子树取最大值

int Depth(BiTree T){
    if(!T){	//空树
        return 0;
    }
    else{	//不是空树，和广义表相似
        depthLeft = depth(T->lchild);
        depthRight = depth(T->rchild);
        return (1 + max(depthLeft,depthRight));
    }
}

3.复制二叉树（后序遍历）

//复制二叉树
BiTNode *GetTreeNode(TElemType item,BiTNode *lptr,BiTNode *rptr){	//生成一个二叉树的结点
    if(!(T=(BiTNode*)malloc(sizeof(BiTNode))))
        exit(1);
    T->data=item;	//数据域
    T->lchild = lptr;	//左指针域
    T->rchild = rptr;	//右指针域
    return T;
}
BiTNode *CopyTree(BiTNode *T){
    if(!T)
        return NULL;
    if(T->lchild)
        newlptr = CopyTree(T->lchild);	//递归复制左子树
    else
        newlptr = NULL;
    if(T->rchild)
        newrptr = CopyTree(T->rchild);	//递归复制右子树
    else
        newrptr = NULL;
    newT = GetTreeNode(T->data,newlptr,newrptr);
    return newT;
}