CSP-有趣的数(数位DP)
题目
问题描述
我们把一个数称为有趣的,当且仅当:
1. 它的数字只包含0, 1, 2, 3,且这四个数字都出现过至少一次。
2. 所有的0都出现在所有的1之前,而所有的2都出现在所有的3之前。
3. 最高位数字不为0。
因此,符合我们定义的最小的有趣的数是2013。除此以外,4位的有趣的数还有两个:2031和2301。
请计算恰好有n位的有趣的数的个数。由于答案可能非常大,只需要输出答案除以1000000007的余数。
输入格式
输入只有一行,包括恰好一个正整数n (4 ≤ n ≤ 1000)。
输出格式
输出只有一行,包括恰好n 位的整数中有趣的数的个数除以1000000007的余数。
样例输入
4
样例输出
3
思路
一直想不出,看了很多的题解才知道。数字的每一位都会被左边的位数影响,第i位数字 = 第i-1位数 + 最后一位数字。从数字第一位开始往后讨论每一位,分情况讨论,分析第i数字前的数字有几种组成情况,一共有以下几种情况:
0:{2}只有2
1:{2,0}
2:{2,3}
3:{2,1,3}
4:{2,0,3}
5:{2,0,1,3}
定义状态d[N][6],d[i][j]表示第i位数的第j种状态
状态转移图:
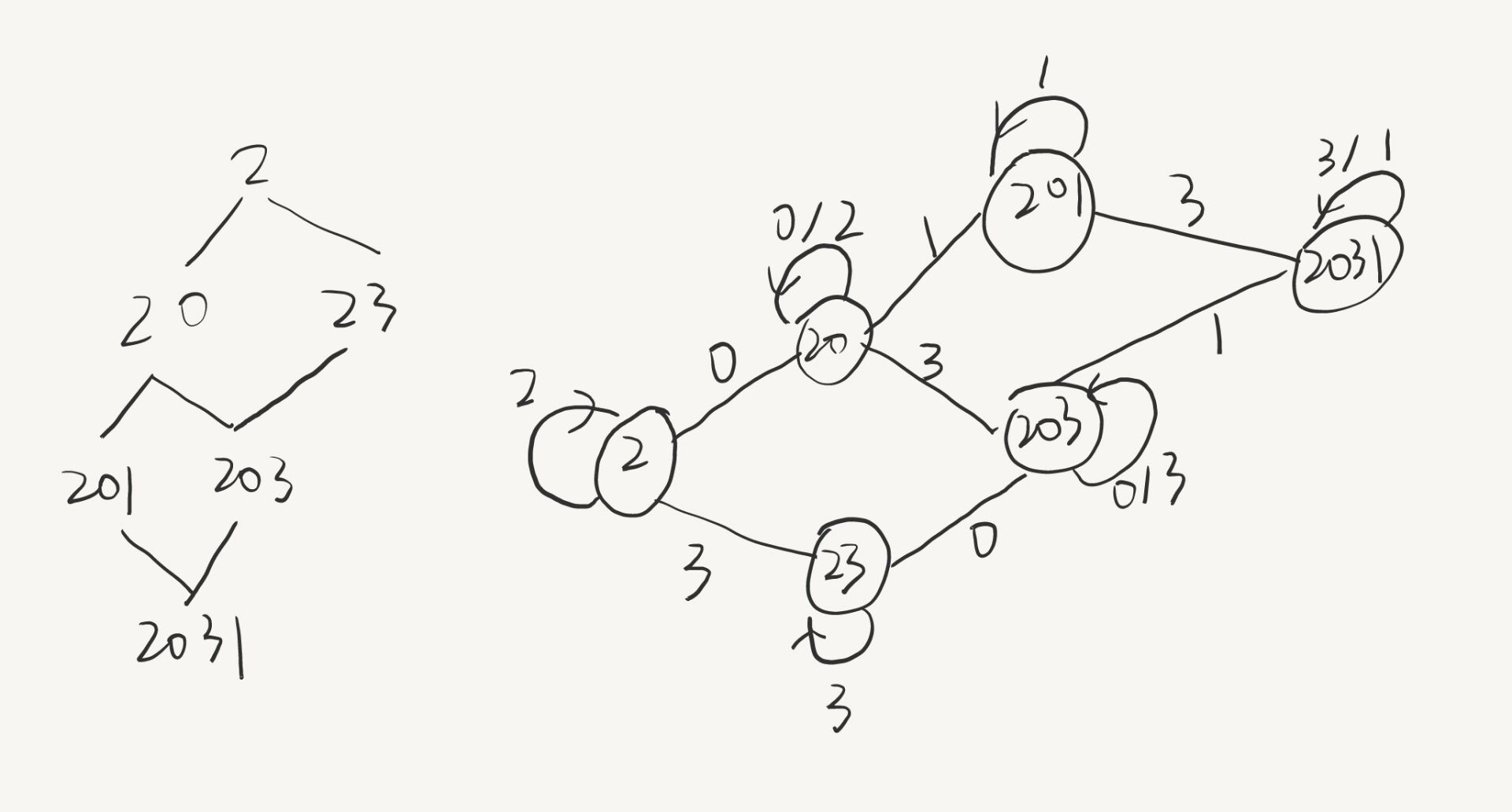
状态转移公式:
dp[i][0]=1
dp[i][1]=dp[i-1][1]*2 + dp[i-1][0]
dp[i][2]=dp[i-1][2] + dp[i-1][0]
dp[i][3]=dp[i-1][3]*2 + dp[i-1][1]
dp[i][4]=dp[i-1][1] + dp[i-1][2] + dp[i-1][4]*2
dp[i][5]=dp[i-1][5]*2 + dp[i-1][4] + dp[i-1][3]
题解(C++)
#include<stdio.h>
#include<iostream>
const int mod = 1e9+7;
long long dp[1010][6];
int main(){
int n;
scanf("%d",&n);
dp[0][0]=1;
for(int i=1;i<n;i++){
dp[i][0]=1;
dp[i][1] = (dp[i-1][1] * 2 + dp[i-1][0])%mod;
dp[i][2] = (dp[i-1][2] + dp[i-1][0])%mod;
dp[i][3] = (dp[i-1][3] * 2 + dp[i-1][1])%mod;
dp[i][4] = (dp[i-1][1] + dp[i-1][2] + dp[i-1][4] * 2)%mod;
dp[i][5] = (dp[i-1][5] * 2 + dp[i-1][4] + dp[i-1][3])%mod;
}
printf("%d",dp[n-1][5]);
return 0;
}


