洛谷入门3-循环结构：回文质数、斐波那契数列

一、回文质数

 

 解题：

 

# include<iostream>
# include<algorithm>
# include<cmath>
using namespace std;


bool isprime(int n)//判断是否是质数
{
    int b=sqrt(n);
    if(n%2==0) return 0;//节约时间
    for(int i=2;i<=b;i++)
    {
        if(n%i==0)
        return 0;
    }
    return 1;
}

bool ispd(int n)//判断是否是回文数
{
    int x=0;
    int k=n;//防止n的值被改变
    while(n)
    {
        x = x*10 + n%10;
        n/=10;
    }
    if(x==k) return 1;
    return 0;
}

int main()
{
    long long a,b;//给出的范围
    cin>>a>>b;
    if(b>=9989899) b=9989899;//一亿以内最大的回文素数
    if(a%2==0) a+=1;
    for(int i=a;i<=b;i+=2)
    {
        if(ispd(i)==0) continue;//先判断是否是回文数
        else if(isprime(i)) cout<<i<<endl;//再判断是否是质数
    }
    return 0;
}

 

 

二、斐波那契数列

 

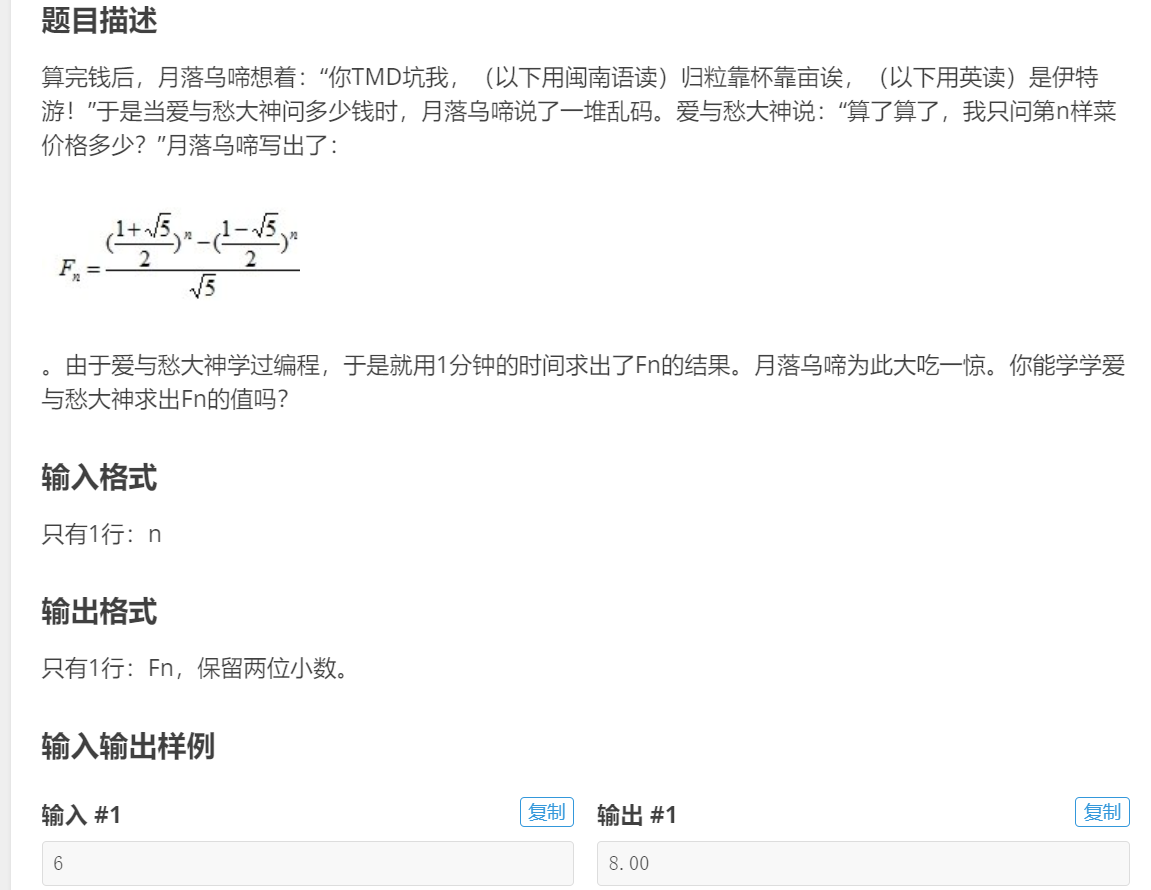
解题：

 

# include<iostream>
# include<iomanip>
using namespace std;


int main()
{
    int n;
    cin>>n;
    long long a=1,b=0,c=0;
    for(int i=1;i<=n;i++)//基本循环
    {
        c=a+b;
        a=b;
        b=c;
    }
    cout<<setprecision(2)<<fixed<<1.0*c;
    return 0;
}