2020牛客暑期多校训练营(第二场) G.Greater and Greater

• 题意

  • 给出两个序列 A、B，其长度分别为 n、m，保证 $n>m $ ，求 A 中有多少个长度为 m 的子串 S，使得\(\forall i\in\{1,2,\cdots,m\},S_i \ge B_i\)

• 解析

  • 出题人直播时表示看到数据很容易想到用 \(bitset\) (雾

  • 对于每一个 \(A_i\) 需要求一个长度为 \(m\) 的 \(bitset\) \(S_i\) ，其中 \(S_i[j] = 1\) 表示 $A_i \ge B_j $ 。

  • 

  • 那么如果得到了所有的 \(S_i\) 该如何判断答案呢

  • 

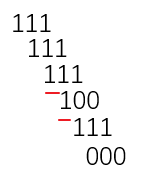
  • 可以发现只有某一列的三个数全为 1 ，才对答案有贡献。做法下面等会讲。

  • 现在我们要考虑的问题就是如何高效地得到所有地 \(S_i\) 。

  • 发现，在对 \(B\) 序列排序后，如果求出 \(B\) 对应的 \(bitset\) \(S_j^‘\)，会发现 \(i\) 位置的 \(bitset\) 和 \(i-1\) 的 \(bitset\) 相比，只在第 \(i\) 大的数的对应位置上多了一个 1。

  • 我们现在对 \(B\) 也进行一次 \(bitset\) 操作，那么如果 \(A[i]\) 值在 \([B[j],B[j+1])\)之间( \(B\) 排序后) ，那么可以求出 \(S_i = S_j^‘\)

  • 那么现在要求 \(S_i\) 只需要二分找到 \(A[i]\) 在 \(B\) 中的位置即可。

  • 在解决了 \(S_i\) 后要考虑如何得到答案，我们发现 \(S_i\) 和 \(S_{i-1}\) 相比，只需要将 \(S_{i-1}\) 右移一位再进行 与 操作，就能把两者相联系起来，那么我们只要维护一个从起始开始的 与 的和 \(ans\)，如果 \(ans[0] = 1\) 那么就对答案有贡献。

  • 注意要先处理好 \(A\) 中前 \(m-1\) 项，而且在 \(ans\) 的每次右移过程中需要将 \(ans[m-1]\) 赋值为 1。不然会影响到之后的判断。

• 代码

  • #include <bits/stdc++.h>
    
    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pii;
    const int Maxb = 10;
    const int Maxa = 2e5+10;
    const int Inf = 0x7f7f7f7f;
    const int Mod = 1e9+7;
    
    vector<pii> v;
    int a[Maxa],b[Maxb];
    bitset<Maxb> Bit[Maxb];
    
    int main(){
        int n,m;
        scanf("%d %d",&n,&m);
        for(int i=1;i<=n;i++)
            scanf("%d",a+i);
        v.push_back(make_pair(0,0));
        for(int i=1;i<=m;i++)
        {
            scanf("%d",b+i);
            v.push_back(make_pair(b[i],i));
        }
        sort(v.begin(),v.end());
        for(int i=1;i<=m;i++)
        {
            Bit[i] = Bit[i-1];
            Bit[i].set(m - v[i].second,1);
        }
        bitset<Maxb> ans;
        for(int i=1;i<m;i++)
        {
            pii cnt;
            cnt = make_pair(a[i],m+1);
            int t = lower_bound(v.begin(),v.end(),cnt) - v.begin() - 1;
            ans >>= 1;
            ans.set(m-1,1);
            ans &= Bit[t];
        }
        int Ans = 0;
        for(int i=m;i<=n;i++)
        {
            pii cnt;
            cnt = make_pair(a[i],m+1);
            int t = lower_bound(v.begin(),v.end(),cnt) - v.begin() - 1;
            ans >>= 1;
            ans.set(m-1,1);
            ans &= Bit[t];
            Ans += ans[0];
        }
        cout<<Ans<<endl;
        return 0;
    }