（模拟）布料仿真的基本方法

本文禁止转载
B站：Heskey0

---

布料仿真的两大类方法：

1. Mass-Spring Damper Model

Pros:

• It is derived from natural tendency and is easier to implement

Cons:

• The model is not derived from theory or observations which makes it less accurate.
• It has too much of coupling among the springs.
• Setting spring constant values to obtain desired effect is difficult

2. Elasticity-Model

By considering the surface of the cloth and integrating all the energy functions a more accurate model was designed called Elasticity Model which includes the following properties:

• There exists a resistance in triangles and edges while making changes to their size. So energy is required if we want to compress or expand them.
• Bending is resisted by the edges. So energy is required if two adjacent faces needs to be bent.
• Deformation is resisted by triangle. So energy is required in deforming or shearing a triangle.

Chapter 1. 中科大

2021年（第九届）中国科学技术大学《计算机图形学前沿》暑期课程_哔哩哔哩_bilibili

1.1 An overview of the cloth simulation

Cloth simulation in known to be slow:

• Dynamics Solver (40% of the total cost)
  • High resolution
  • High nonlinearity: 布料抗拉伸却易弯曲
  • High stiffness
• Collision Handling (60% of the total cost)
  • Collision detection
  • Collision response

1.1.1 时间积分

Backward Euler Integration/ implicit Euler:

$$\begin{aligned} x^{t+\Delta t}&=x^t+\Delta tv^{t+\Delta t}\\ v^{t+\Delta t}&=v^t+\Delta tM^{-1}f(x^{t+\Delta t}) \end{aligned}$$

可推出：

$$\begin{aligned} x^{t+\Delta t}&=x^t+\Delta tv^t+\Delta t^2M^{-1}f(x^{t+\Delta t})\\ v^{t+\Delta t}&=v^t+\frac1{\Delta t}(x^{t+\Delta t}-x^t) \end{aligned}$$

上式等价于一个优化问题（对下面的$F(X)$求导即可证明）：

重新构建一个Nonlinear optimization:（也可以构建关于 $v^{t+\Delta t}$ 的优化问题）

$$x^{t+\Delta t}=\arg\min_xF(x)$$

where: (加号左边是kinetic energy，右边是potential energy)

$$F(x)=\frac1{2\Delta t^2}(x-\bar x)^TM(x-\bar x)+E(x)$$

and

$$\bar x=x^t+\Delta tv^t$$

1.1.2 Collision Handing

discrete collision handling:

• 只保证每一个状态都处于安全状态
• 不保证是否发生碰撞

碰撞是一个约束：

$$x^{t+\Delta t}=\arg\min_xF(x)\\ s.t.\quad x^{t+\Delta t}\in\Omega$$

where:

• $\Omega$: intersection-free region

continuous collision handling:

$$x^{t+\Delta t}=\arg\min_xF(x)\\ s.t.\quad sx^t+(1-s)x^{t+\Delta t}\in\Omega,\quad\forall s\in[0,1]$$

1.2 (basic method) Popular methods for real-time cloth simulation

1.2.1 非线性优化的套路

非线性优化的solver，通常是满足以下形式：

An iterative nonlinear solver typically has the form: (with certain acceleration methods)

$$x^{(k+1)}=x^k-\alpha^{(k+1)}(A^{(k+1)})^{-1}\frac{\part F(x^{k})}{\part x}$$

where:

• step size: $\alpha$
• matrix: $A$
• gradient: ${\part F(x^{k})}/{\part x}$

1.2.2 Newton-Raphson

Newton-Raphson中，$A$ 是一个Hessian matrix：

$$A^{(k+1)}=\frac{\part^2 F(x^{k})}{\part x^2}$$

Pros (优点):

• 2rd-order convergence rate. (单位时间内，error=error/2)

Cons (缺点):

• How to solve $A^{-1}$ 或者说 $A^{-1}f$ ?

  • Direct, Iterative (PCG)

• It can fail to converge if $x$ is far from the solution

  • small step size
  • Hessian must be enforced to be positive define
    • 很多迭代法要求矩阵是positive define的

Newton-Raphson方法的应用：

Papers:

• (1996) Large step on cloth simulation: 只用了一次Newton iteration

Marvelous Designer (mostly CPU, has GPU)

• 一次Newton iteration solved by limited PCG iterations

1.2.3 Gradient Descent

Gradient Descent中，$A$ 是一个identity matrix：

$$A^{(k+1)}=I$$

Pros:

• Very GPU friendly
• Very simple

Cons:

• 1st-order convergence rate (收敛很慢)
• No simulator uses this as it is.

1.2.4 Projective Dynamics

Projective Dynamics中，$A$ 是一个Constant smoothing matrix:

$$A^{(k+1)}=C$$

Pros:

• Fast on CPUs, since $C$ can be pre-factorized. (在CPU上对 $C$ 做预分解)
• Fast convergence in the first few iterations
  • Intuitively, the use of $C$ quickly smooths out some low-frequency errors.

Cons:

• Not GPU-friendly
  • 矩阵的inverse，通常不是sparse matrix。会导致矩阵乘法效率慢
• 1st-order convergence rate: slow convergence overall. (一开始收敛快，然后像gradient descent一样收敛慢)

1.2.5 Diagonal Hessian

(sig asia 2015)Diagonal Hessian中，$A$ 是一个Hessian matrix的diagonal matrix:

$$A^{(k+1)}=diag\left(\frac{\part^2 F(x^{k})}{\part x^2}\right)$$

Pros:

• Converges faster than gradient descent
• GPU friendly

Cons:

• Still does not converge that fast

1.3 (Acceleration) Popular methods for real-time cloth simulation

有了非线性算法，还需要加速算法，如：

• (2015) Chebyshev
• (2015) Nesterov
• (2018) Anderson
• (2017) L-BFGS

Only Chebyshev is GPU-friendly. Multiscale acceleration is also effective

1.3.1 Chebyshev

算法：

• For $k=0,...,K$

  • $$x^{(k+1)}=x^k-\alpha^{(k+1)}(A^{(k+1)})^{-1}\frac{\part F(x^{k})}{\part x}$$

  • if $k==0$ then $\omega=1$

  • if $k==1$ then $\omega=2/(2-\rho)^2$

  • if $k>1$ then $\omega=4/(4-\rho^2\omega)$

  • $x^{(k+1)}=\omega x^{(k+1)}+(1-\omega)x^{(k-1)}$

$\rho$ is the spectral radius, i.e. the estimation of the residual error decreasing rate

For example:

• 某次迭代，error=error*0.99，则 $\rho\approx 0.99$

推荐套路：

• CPU:
  • Projective dynamics followed by Newton-Raphson
• GPU:
  • Chebyshev + Diagonal Hessian
  • Newton-Raphson with PCG

1.4 The remaining topics

1.4.1 Position-Based Dynamics

不去解数学问题：

$$x^{(k+1)}=x^k-\alpha^{(k+1)}(A^{(k+1)})^{-1}\frac{\part F(x^{k})}{\part x}$$

而是通过直接将两个顶点拉近，修改顶点的位置（非物理）

Pros:

• No physical quantities
• Everything on GPU shared memory, fast! (NVcloth)
  • 当顶点少的时候，直接将顶点数据放到shared memory中，访问快

Cons:

• No physical meaning
• Not scalable. (Shared memory is only 16kB)
  • vertex多的时候，效率会显著下降

Chapter 2. Games103

1. 建模

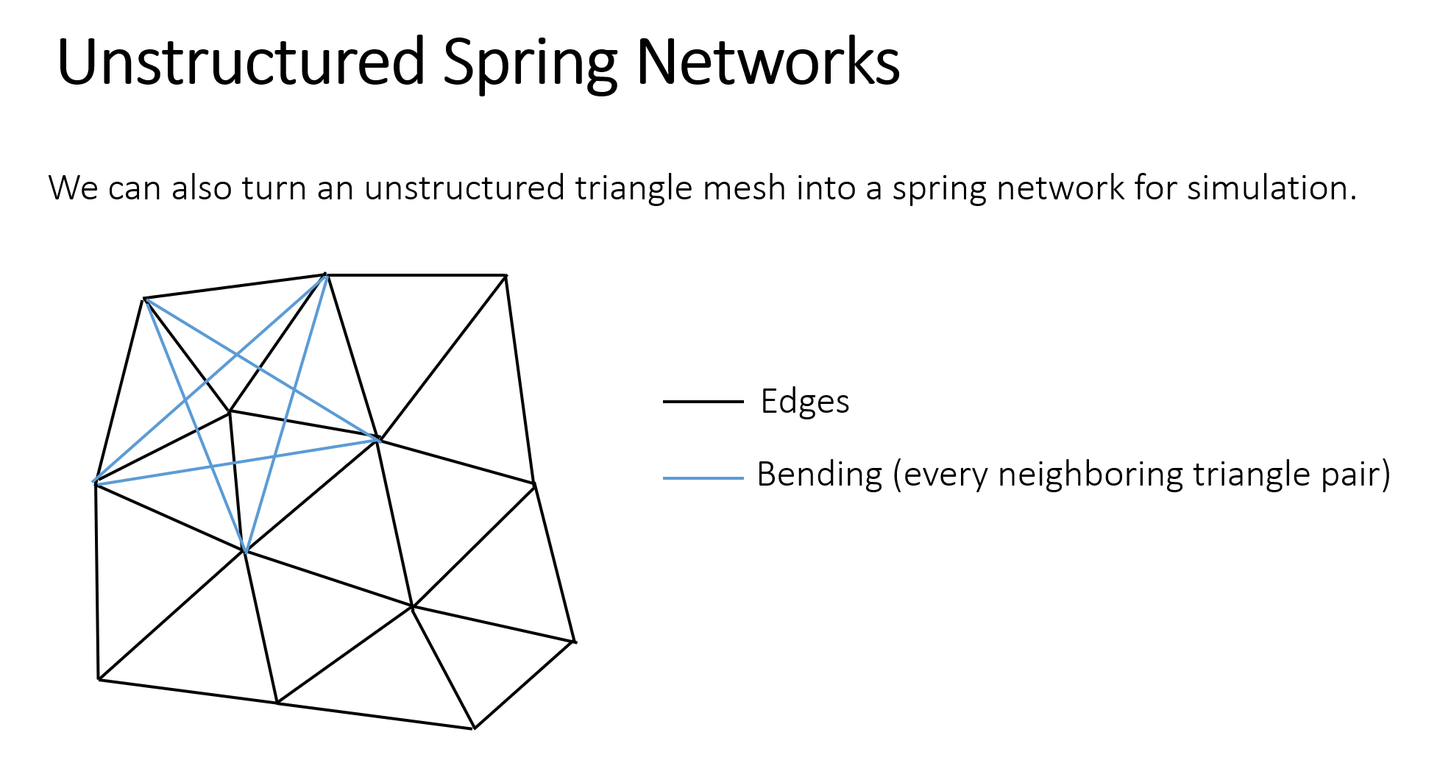
1.1 建立弹簧

在三角网格的每个边上都加一根弹簧，然后跨过所有内部边添加弹簧（称任意两个相邻三角形的公共边为内部边，两个相邻三角形组成一个四边形，新添加的弹簧为这个四边形的对角线）来抵抗弯曲

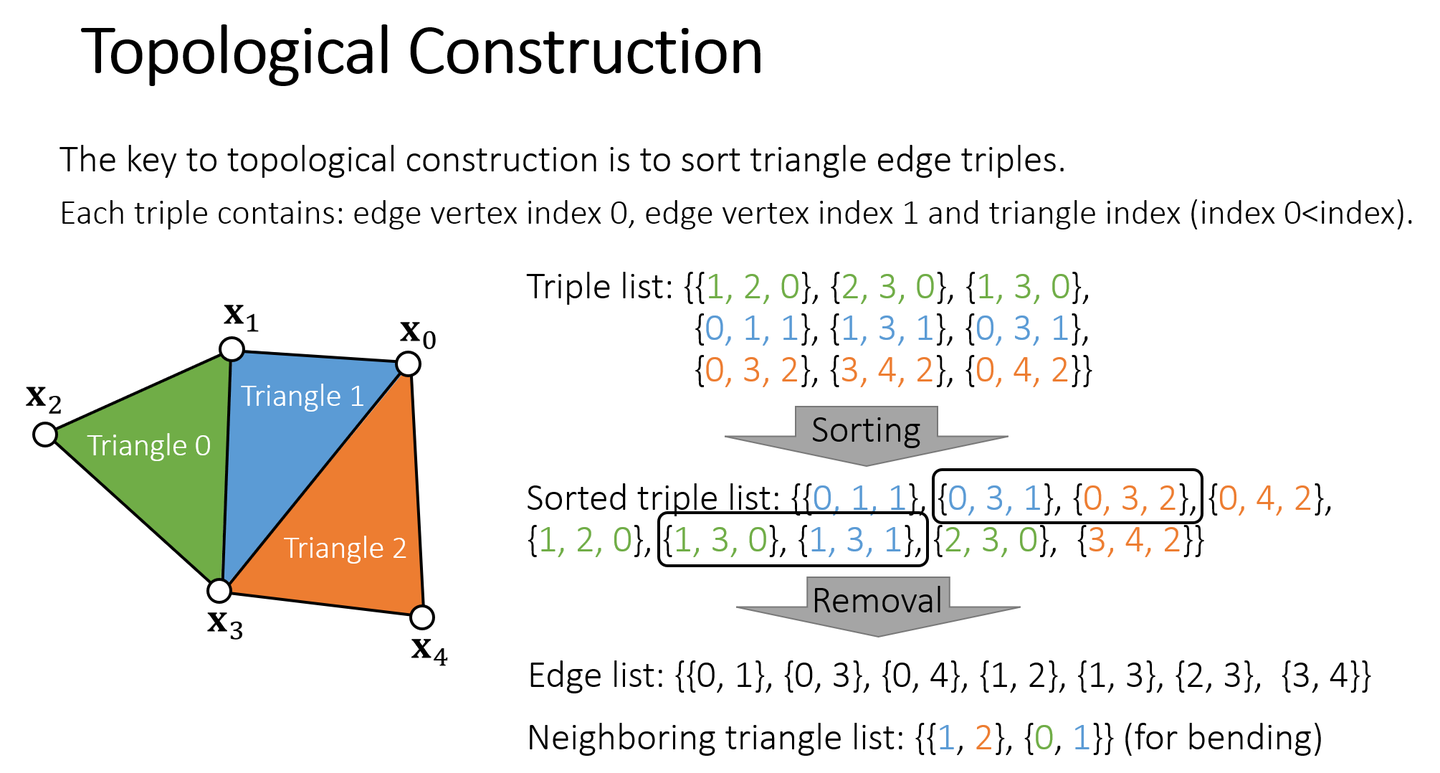
边数组（Triple list）的建立：

弹簧的建立：

• 对于三角形边上的弹簧，直接遍历 Edge list，依次添加弹簧即可。

• 对于跨过内部边的弹簧，查询内部边所在三角形的剩余两个顶点，把它们连接起来即可。

1.2 Spring Hessian

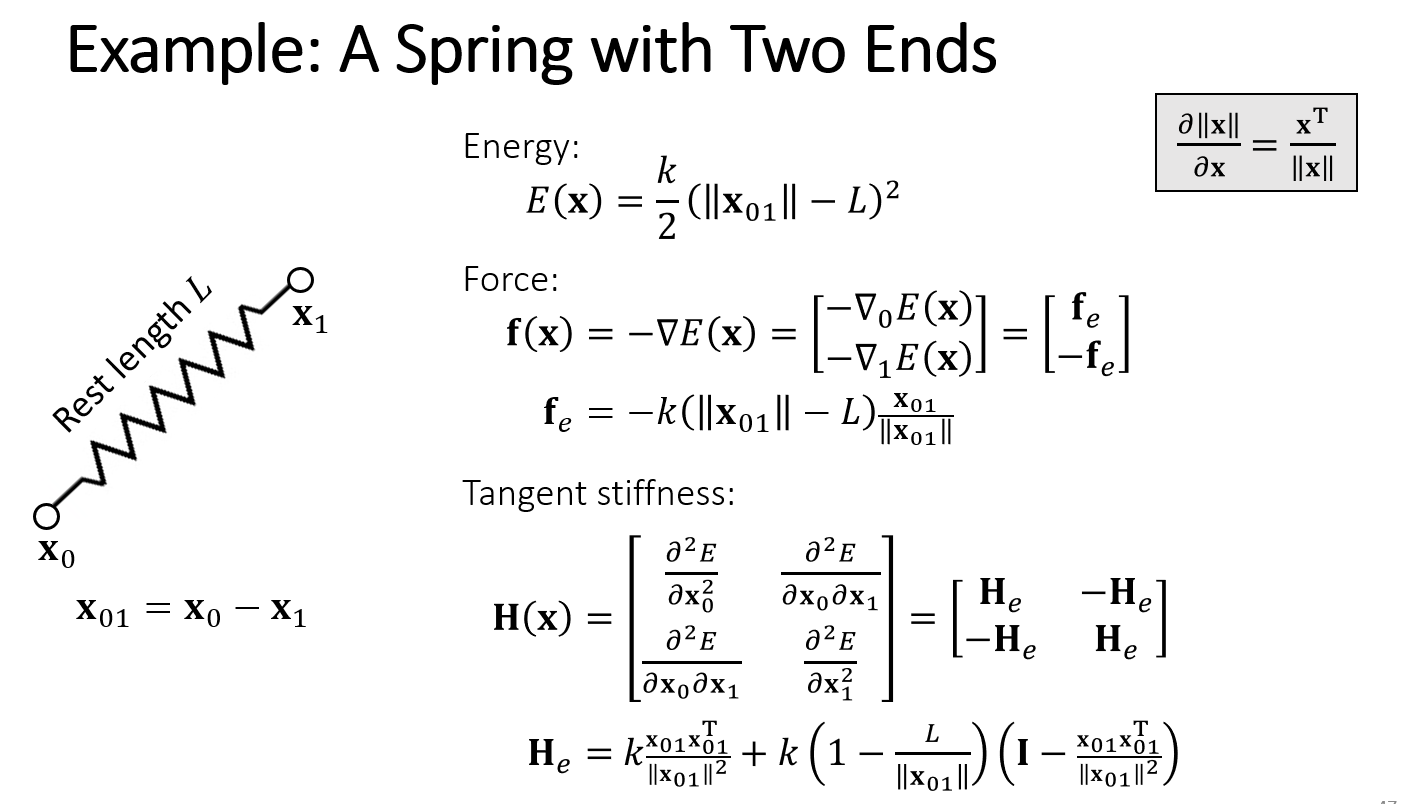
为了计算：

$$H=\frac{\part f}{\part x}$$

需要先计算Sprint Hessian：

$$H_e=k\frac{x_{01}x_{01}^T}{||x_{01}||^2}+k\left(1-\frac{L}{||x_{01}||}\right)\left(I-\frac{x_{01}x_{01}^T}{||x_{01}||^2}\right)$$

也可以写成：

$$H_e=k\left[I-\frac{L}{||x_{01}||}\left(I-\frac{x_{01}x_{01}^T}{||x_{01}||^2}\right)\right]$$

小矩阵 $H_e$ 组成大矩阵 $H$，对角线上的 $H_e$ 要带上负号

2. Simulation by Newton's Method

$$x^{(k+1)}=x^k-\alpha^{(k+1)}\left(\frac{\part^2 F(x^{k})}{\part x^2}\right)^{-1}\frac{\part F(x^{k})}{\part x}$$

其中：

$$F(x)=\frac1{2\Delta t^2}(x-\bar x)^TM(x-\bar x)+E(x)$$

where:

$$\bar x=x^t+\Delta tv^t$$

则

$$\nabla F(x^{(k)})=\frac1{\Delta t^2}M(x^{(k)}-x^{[0]}-\Delta tv^{[0]})-f(x^{(k)})$$

and

$$\frac{\part^2 F(x^{k})}{\part x^2}=\frac1{\Delta t^2}M+H(x^{(k)})$$

where:

• $H(x^{(k)})$ 就是弹簧系统 $E(x)$ 的Hessian，
  • 弹簧拉伸时，$H(x)$一定是SPD，$\frac{\part^2 F(x^{k})}{\part x^2}$ 一定是SPD，$F(x)$ 只有一个最小值，牛顿法收敛到唯一的解
  • 弹簧压缩时，$H(x)$可能不是SPD，$\frac{\part^2 F(x^{k})}{\part x^2}$ 可能不是SPD

Algorithm:

1. Initialize

2. For $k=0,...,K$

   1. Solve

      $$\left(\frac1{\Delta t^2}M+H(x^{(k)})\right)\Delta x=-\frac1{\Delta t^2}M(x^{(k)}-x^{[0]}-\Delta tv^{[0]})+f(x^{(k)})$$

   2. $x^{(k+1)}\leftarrow x^{(k)}+\Delta x$

3. $x^{[1]}=x^{(k+1)}$

4. $v^{[1]}\leftarrow(x^{[1]}-x^{[0]})/\Delta t$

where:

• $x^{[0]}$: 上一帧位置
• $x^{[1]}$: 这一帧位置
• $x^{(k)}$, $x^{(k+1)}$: 上一次/这一次迭代的位置

large step in cloths simulation中的方法：[游戏物理探秘]理解Large Steps in Cloth Simulation - 知乎

• 通过backward Euler的推导，得出：

  $$(I-hM^{-1}\frac{\part f}{\part v}-h^2M^{-1}\frac{\part f}{\part x})\Delta v=hM^{-1}(f_0+h\frac{\part f}{\part x}v_0)$$

• 解上面的线性系统 $Ax=b$.

3. 主流模拟方法

3.1 基于物理的模拟

1. Mass-spring system

   1. Stretching

   2. Bending Issue

      1. Dihedral angle model

   3. Locking Issue

      1. 本质上，由于自由度缺失，Bending和Stretching不独立

   4. Stiffness Issue

      1. 问题：当stifness大的时候

         1. 显式积分不稳定，需要减小time step

         2. 隐式积分ill-condition，需要增加迭代次数

            • 要解决这些问题，计算量会增大

3.2 非物理的模拟

要满足约束：

$$\phi(x_i,x_j)=||x_i-x_j||-L=0$$

$L$是弹簧的原长

投影的思路：使用投影函数，将不满足约束的顶点投影到约束内

投影的方式：Gauss-Seidel，Jacobi

1. Position Based Dynamic：弹性由迭代数量，网格精度体现（顶点多，迭代数量多，则布料会显得更有弹性）

   1. 过程：

      1. 先让粒子自由运动
      2. 投影修改粒子的位置，使粒子满足约束

   2. 投影的方式：

      1. Jacobi迭代

      2. GS迭代

   3. 优点：GPU并行

   4. 缺点

      1. 没有物理含义
      2. 顶点多的时候解算很慢，收敛慢
      3. 迭代过多会导致Locking Issue

      解决方案，构建不同分辨率的布料，解算低分辨率的，然后将结果传到高分辨率网格

2. Strain Limiting（形变约束）

   1. 过程：

      1. 先进行模拟
      2. 投影修改粒子的位置（相当于纠错），使粒子满足约束（把约束放宽）

   2. Spring Strain Limiting（一维的Strain Limiting）

      1. $$\sigma^{min}<\phi(x)<\sigma^{max}$$

      2. 或者写成

      3. $$\sigma^{min}<\frac1L||x_i-x_j||<\sigma^{max}$$

      4. （当 $σ=1$ 的时候，就是PBD）

   3. Triangle Area Limiting

      1. 当三角的面积超出了约束范围时，直接对三角形进行缩放使面积满足约束。

3. Projective Dynamic

   1. 过程：

      1. 先让粒子自由运动

      2. 投影得到新的粒子位置 ，然后用粒子新旧位置更新能量（和原始mass-spring system的力的公式一样）

         $$E(x)=\sum\frac k2(||x_i-x_j||-L_e)^2$$

      3. 然后依然使用隐式积分

   2. 使用Projective Dynamic，能量的Hessian更简单（常数矩阵）

      $$f=\nabla E=-k\sum(||x_i-x_j||-L_e)\frac{x_i-x_j}{||x_i-x_j||}$$

   3. 优缺点：

      1. 有物理意义
      2. GPU上运行慢
      3. 迭代一开始收敛快，之后收敛慢

4. Constrained Dynamic

   1. 在隐式积分中引入了对偶变量便于模拟劲度 k 较大的情况

4. Issue

4.1 Locking Issue

Locking Issue: 当Stiffness大时，布料拉不动，也不能弯曲。（比如纸：拉不动，但能弯曲）

解决方法：

1. 减小弹簧压缩时的弹性系数
2. 使弹簧可以在一定范围内自由移动，超出范围才开始计算弹力

5. Collision Handling

《GPU Gems 3》Chapter 32

3.1 Collision Culling

Spatial Partitioning/Spatial Hashing（对空间划分）

• Morton code：https://www.bilibili.com/video/BV12Q4y1S73g?p=9&vd_source=10edfdf73ab80a5b21d82f049d07a937&t=1947.3
  • 使划分后的格子，在内存上访问连续
• GPU friendly，易于实现
• 物体运动后，需要重新计算（计算消耗高）

BVH（对物体划分）

• self-colision的处理
• 不易于实现，Not GPU friendly（GPU不易存储树）
• 更新树时，不需要更新树的结构，只需要更新bounding volumes

3.2 Collision Test

Discrete Collision Detection（DCD）

• Edge-triangle pairs
• 只检测某状态是否相交，不能检测穿透

Continuous Collision Detection

• Vertex-triangle pairs

  • vertex和triangle构成的四面体，面积为0
  • 每个顶点位置都是 $t$ 的一次函数，解一元三次方程（用二分法，3个顶点所以是三次方程）判断四面体面积为0时（即vertex和triangle在同一平面），vertex是否在triangle内

• Edge-edge pairs

• 难写，性能消耗大，游戏GPU以单浮点精度为主

碰撞处理：

• Interior point method

  • 每一次运动后都满足碰撞约束
  • 慢（需要处理所有vertex）
  • Always succeed

• Impact zone optimization

  • 逃出约束之后，再慢慢纠正
  • 快（只需要处理碰撞的vertex）
  • May not succeed

课后阅读论文：Robust Treatment of Collisions, Contact and Friction for Cloth Animation(TOG SIGGRAPH 2002)