【Computer Graphics】基础光线追踪中的采样

本文未经允许禁止转载
B站：https://space.bilibili.com/455965619
作者：Heskey0

因为Graphics领域书籍和资料以英文为主，故本文将以英文的方式呈现。

---

path tracer based on 《PBRT》

一.introduction to sampling theory

1. what is sampling?

impulse train：

sampling process corresponds to multiplying the function by a “impulse train” function, an infinite sum of equally spaced delta functions.

《PBRT》A digital image is represented as a set of pixel values, typically aligned on a rectangular grid. When a digital image is displayed on a physical device, these values are used to determine the spectral power emitted by pixels on the display.

《PBRT》the pixels that constitute an image are point samples of the image function at discrete points on the image plane.

there is no “area” associated with a pixel.

when sampling the film signal

pos = camera_pos
ray_dir = ti.Vector([
            (2 * fov * (u) / resolution[1] - fov * resolution[0] / resolution[1] - 1e-5),
            2 * fov * (v) / resolution[1] - fov - 1e-5, -1.0
        ]).normalized()

then we need anti-aliazing

pos = camera_pos
ray_dir = ti.Vector([
            (2 * fov * (u + ti.random()) / resolution[1] - fov * resolution[0] / resolution[1] - 1e-5),
            2 * fov * (v + ti.random()) / resolution[1] - fov - 1e-5, -1.0
        ]).normalized()

二.sampling

Preview (CDF sampling technique)

There are many techniques for generating random variates from a specified probability distribution such as the normal, exponential, or gamma distribution. However, one technique stands out because of its generality and simplicity: the inverse CDF sampling technique.

1. Uniformly Sampling a Hemisphere (multidimensional sampling technique)

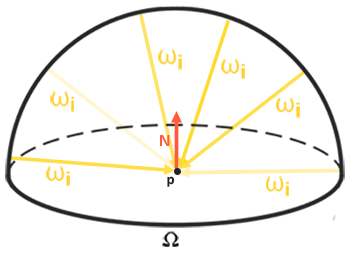
a uniform distribution means that the density function is a constant, so we know that p(x) = c

so p(ω) = 1/2*pi

then p(θ, φ) = sinθ/2*pi

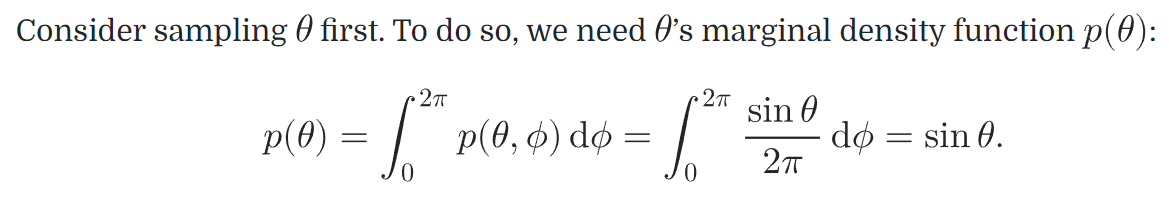
Notice that the density function for φ itself is uniform

then use the 1D inversion technique to sample each of these PDFs in turn

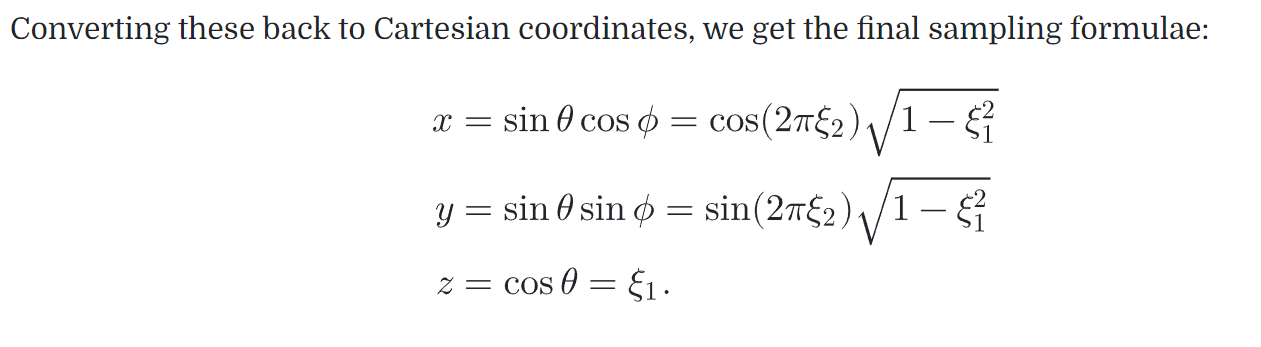
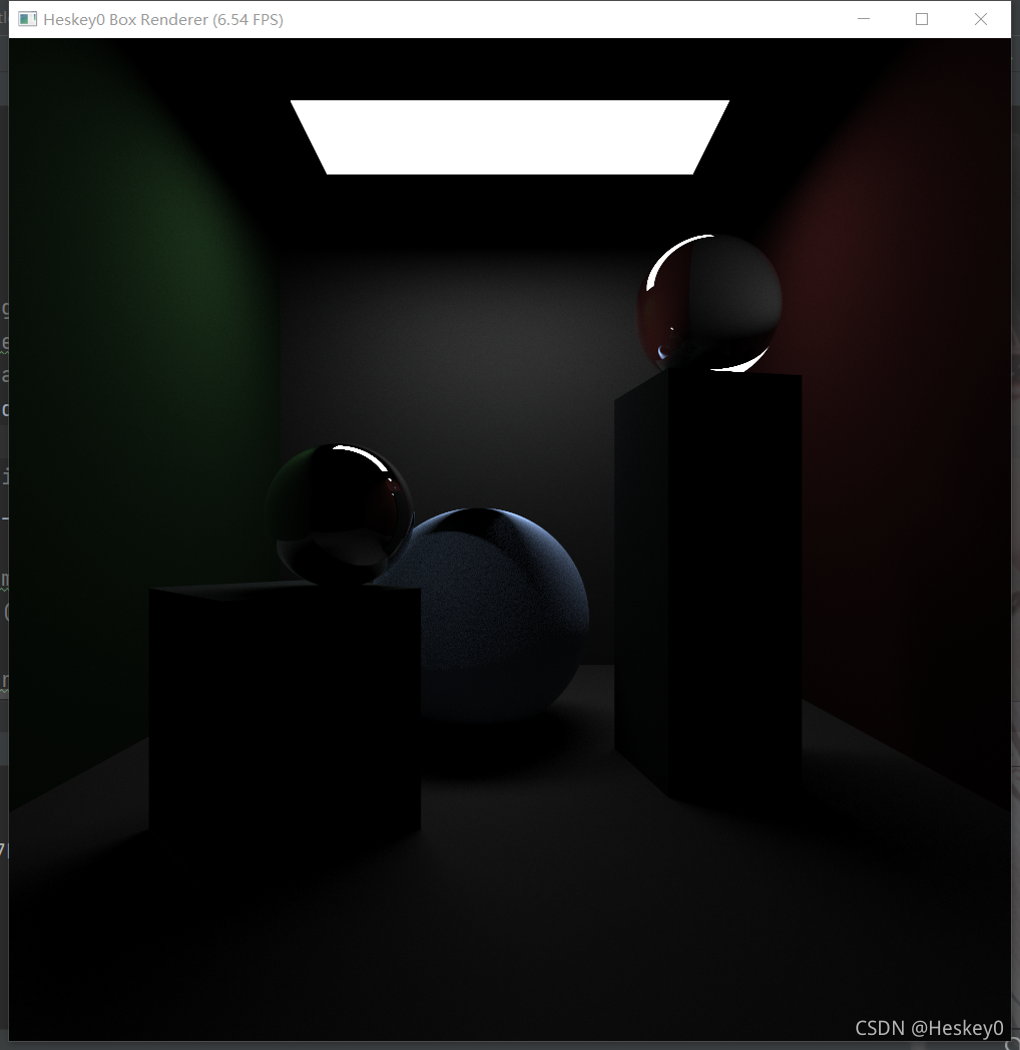
2. sample area light

def sample_area_light(hit_pos, pos_normal):
    # sampling inside the light area
    x = ti.random() * light_x_range + light_x_min_pos
    z = ti.random() * light_z_range + light_z_min_pos
    on_light_pos = ti.Vector([x, light_y_pos, z])
    return (on_light_pos - hit_pos).normalized()

3. introduction to importance sampling

why we need importance sampling?

the Monte Carlo estimator converges more quickly if the samples are taken from a distribution p(x) that is similar to the function f(x) in the integrand.

《PBRT》：We will not provide a rigorous proof of this fact but will instead present an informal and intuitive argument.

then we try to analyze the importance sampling method

we have three terms

• BRDF
• incident radiance ( infeasible )
• cosine term

4. cosine-weighted sampling

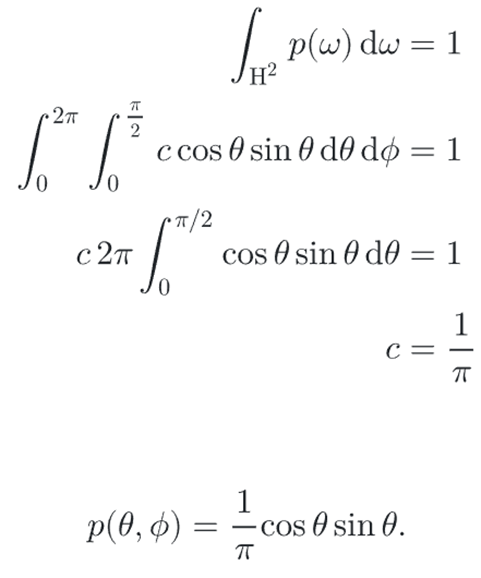
Malley's method

So, We could compute the marginal and conditional densities as before, but instead we can use a technique known as Malley’s method to generate these cosine-weighted points.

1. cosine term

2. 2D Sampling with Multidimensional Transformations

   • (1) sampling a unit disk (Concentric Mapping)

   • (2) project up to the unit hemisphere (cosine-weighted hemisphere sampling)

(1) sampling a unit disk

(2) projection

To complete the (r,φ)=(sinθ,φ)⇒(θ,φ) transformation, we need the determinant of the Jacobian

Why

5. multiple importance sampling

BDPT only：

BDPT + MIS：

Why we need MIS?

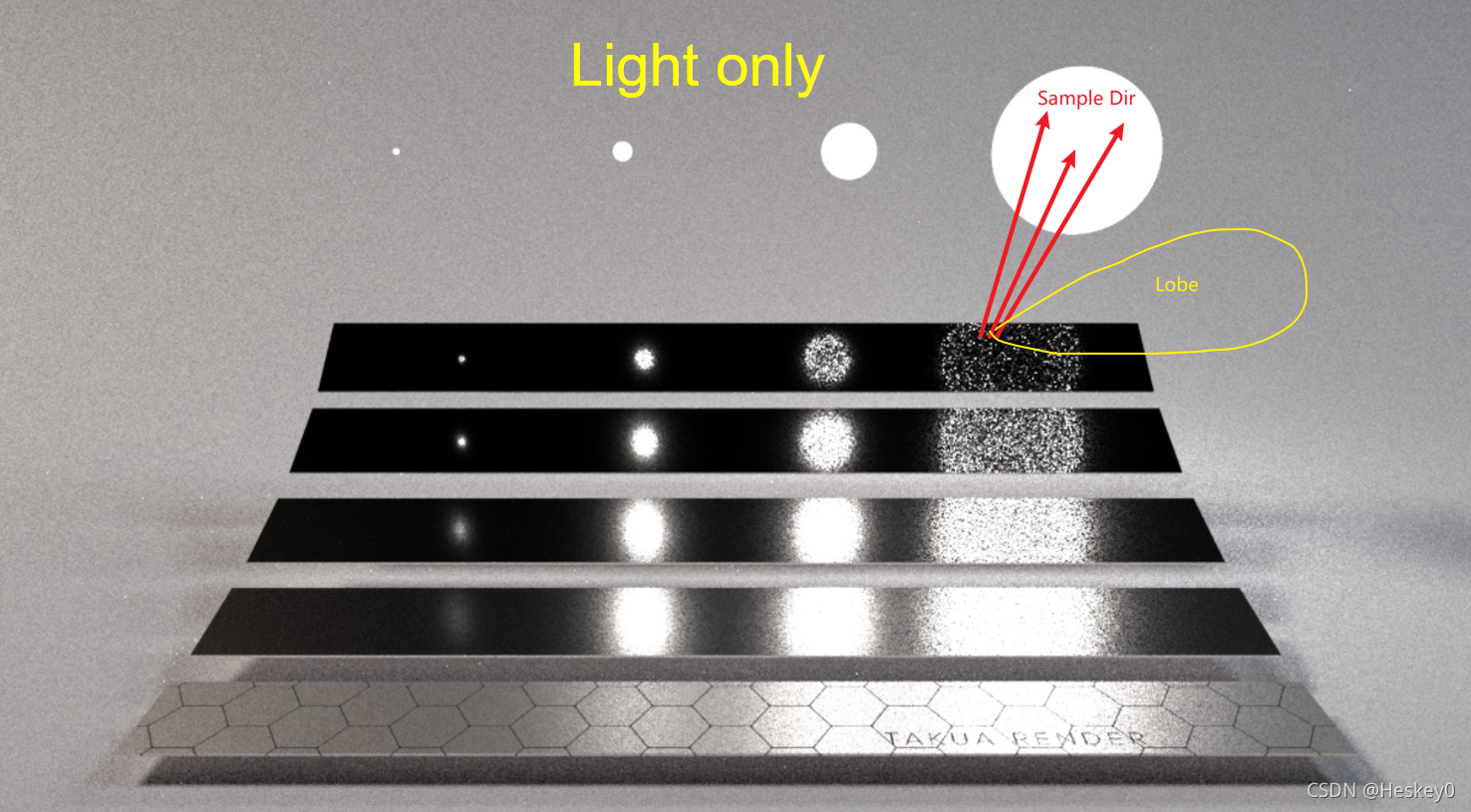
• balance heuristic

• power heuristic (Veach determined empirically that β=2 is a good value.)

本文未经允许禁止转载
B站：https://space.bilibili.com/455965619
作者：Heskey0