数学基础之概率统计
3-1、为什么使用概率?
概率论是用于表示不确定性陈述的数学框架,即它是对事物不确定性的度量。
在人工智能领域,我们主要以两种方式来使用概率论。首先,概率法则告诉我们AI系统应该如何推理,所以我们设计一些算法来计算或者近似由概率论导出的表达式。其次,我们可以用概率和统计从理论上分析我们提出的AI系统的行为。
计算机科学的许多分支处理的对象都是完全确定的实体,但机器学习却大量使用概率论。实际上如果你了解机器学习的工作原理你就会觉得这个很正常。因为机器学习大部分时候处理的都是不确定量或随机量。
 3-2、随机变量
3-2、随机变量
随机变量可以随机地取不同值的变量。我们通常用小写字母来表示随机变量本身,而用带数字下标的小写字母来表示随机变量能够取到的值。例如,
对于向量值变量,我们会将随机变量写成X,它的一个值为。就其本身而言,一个随机变量只是对可能的状态的描述;它必须伴随着一个概率分布来指定每个状态的可能性。
随机变量可以是离散的或者连续的。
 3-3、概率分布
3-3、概率分布
给定某随机变量的取值范围,概率分布就是导致该随机事件出现的可能性。
从机器学习的角度来看,概率分布就是符合随机变量取值范围的某个对象属于某个类别或服从某种趋势的可能性。
 3-4、条件概率
3-4、条件概率
很多情况下,我们感兴趣的是某个事件在给定其它事件发生时出现的概率,这种概率叫条件概率。
我们将给定时
发生的概率记为
,这个概率可以通过下面的公式来计算:
 3-5、贝叶斯公式
3-5、贝叶斯公式
先看看什么是“先验概率”和“后验概率”,以一个例子来说明:
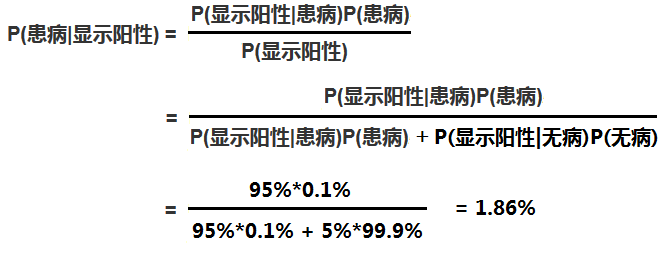
假设某种病在人群中的发病率是0.001,即1000人中大概会有1个人得病,则有: P(患病) = 0.1%;即:在没有做检验之前,我们预计的患病率为P(患病)=0.1%,这个就叫作"先验概率"。
再假设现在有一种该病的检测方法,其检测的准确率为95%;即:如果真的得了这种病,该检测法有95%的概率会检测出阳性,但也有5%的概率检测出阴性;或者反过来说,但如果没有得病,采用该方法有95%的概率检测出阴性,但也有5%的概率检测为阳性。用概率条件概率表示即为:P(显示阳性|患病)=95%
现在我们想知道的是:在做完检测显示为阳性后,某人的患病率P(患病|显示阳性),这个其实就称为"后验概率"。
而这个叫贝叶斯的人其实就是为我们提供了一种可以利用先验概率计算后验概率的方法,我们将其称为“贝叶斯公式”,如下:
在这个例子里就是:
 贝叶斯公式贯穿了机器学习中随机问题分析的全过程。从文本分类到概率图模型,其基本分类都是贝叶斯公式。
贝叶斯公式贯穿了机器学习中随机问题分析的全过程。从文本分类到概率图模型,其基本分类都是贝叶斯公式。
这里需要说明的是,上面的计算中除了利用了贝叶斯公式外,还利用了“全概率公式”,即:
 3-6、期望
3-6、期望
在概率论和统计学中,数学期望是试验中每次可能结果的概率乘以其结果的总和。它是最基本的数学特征之一,反映随机变量平均值的大小。
假设X是一个离散随机变量,其可能的取值有:,各个取值对应的概率取值为:
,则其数学期望被定义为:
假设X是一个连续型随机变量,其概率密度函数为则其数学期望被定义为:
 3-7、方差
3-7、方差
概率中,方差用来衡量随机变量与其数学期望之间的偏离程度;统计中的方差为样本方差,是各个样本数据分别与其平均数之差的平方和的平均数。数学表达式如下:
 3-8、协方差
3-8、协方差
在概率论和统计学中,协方差被用于衡量两个随机变量X和Y之间的总体误差。数学定义式为:

3-9、常见分布函数
1)0-1分布
0-1分布是单个二值型离散随机变量的分布,其概率分布函数为:
2)几何分布
几何分布是离散型概率分布,其定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。即:前k-1次皆失败,第k次成功的概率。其概率分布函数为:
性质:
3)二项分布
二项分布即重复n次伯努利试验,各次试验之间都相互独立,并且每次试验中只有两种可能的结果,而且这两种结果发生与否相互对立。如果每次试验时,事件发生的概率为p,不发生的概率为1-p,则n次重复独立试验中发生k次的概率为:
性质:
4)高斯分布
高斯分布又叫正态分布,其曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,如下图所示:

若随机变量X服从一个数学期望为,方差为
的正态分布,则我们将其记为:
。其期望值
决定了正态分布的位置,其标准差
(方差的开方)决定了正态分布的幅度。
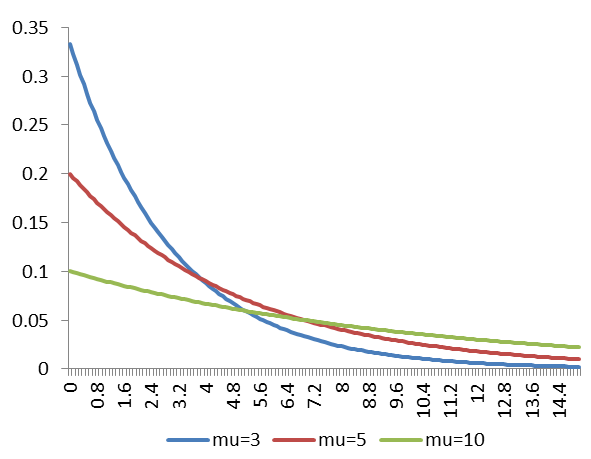
5)指数分布
指数分布是事件的时间间隔的概率,它的一个重要特征是无记忆性。例如:如果某一元件的寿命的寿命为T,已知元件使用了t小时,它总共使用至少t+s小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等。下面这些都属于指数分布:
- 婴儿出生的时间间隔
- 网站访问的时间间隔
-
奶粉销售的时间间隔
指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间t,就等同于t之内没有任何婴儿出生,即:
则:
如:接下来15分钟,会有婴儿出生的概率为:
指数分布的图像如下:
6)泊松分布
日常生活中,大量事件是有固定频率的,比如:
- 某医院平均每小时出生3个婴儿
- 某网站平均每分钟有2次访问
-
某超市平均每小时销售4包奶粉
它们的特点就是,我们可以预估这些事件的总数,但是没法知道具体的发生时间。已知平均每小时出生3个婴儿,请问下一个小时,会出生几个?有可能一下子出生6个,也有可能一个都不出生,这是我们没法知道的。
泊松分布就是描述某段时间内,事件具体的发生概率。其概率函数为:
其中:
P表示概率,N表示某种函数关系,t表示时间,n表示数量,1小时内出生3个婴儿的概率,就表示为 P(N(1) = 3) ;λ 表示事件的频率。
还是以上面医院平均每小时出生3个婴儿为例,则;
那么,接下来两个小时,一个婴儿都不出生的概率可以求得为:
同理,我们可以求接下来一个小时,至少出生两个婴儿的概率:
【注】上面的指数分布和泊松分布参考了阮一峰大牛的博客:“泊松分布和指数分布:10分钟教程”,在此说明,也对其表示感谢!
 3-10、Lagrange乘子法
3-10、Lagrange乘子法
对于一般的求极值问题我们都知道,求导等于0就可以了。但是如果我们不但要求极值,还要求一个满足一定约束条件的极值,那么此时就可以构造Lagrange函数,其实就是把约束项添加到原函数上,然后对构造的新函数求导。对于一个要求极值的函数
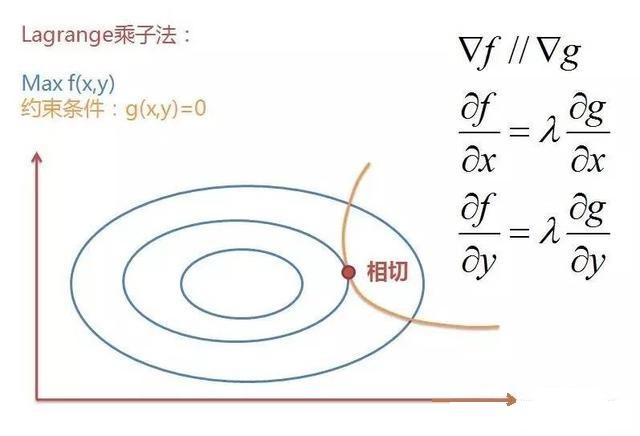
也就是说和
相切,或者说它们的梯度▽
和▽
平行,因此它们的梯度(偏导)成倍数关系;那我么就假设为
倍,然后把约束条件加到原函数后再对它求导,其实就等于满足了下图上的式子。
 3-11、最大似然法
3-11、最大似然法
最大似然也称为最大概似估计,即:在“模型已定,参数θ未知”的情况下,通过观测数据估计未知参数θ 的一种思想或方法。
其基本思想是: 给定样本取值后,该样本最有可能来自参数为何值的总体。即:寻找
使得观测到样本数据的可能性最大。
举个例子,假设我们要统计全国人口的身高,首先假设这个身高服从服从正态分布,但是该分布的均值与方差未知。由于没有足够的人力和物力去统计全国每个人的身高,但是可以通过采样(所有的采样要求都是独立同分布的),获取部分人的身高,然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。
求极大似然函数估计值的一般步骤:
- 1、写出似然函数;
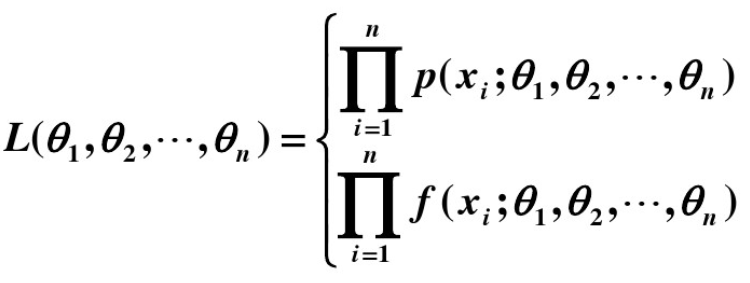
- 2、对似然函数取对数;
- 3、两边同时求导数;
-
4、令导数为0解出似然方程。
最大似然估计也是统计学习中经验风险最小化的例子。如果模型为条件概率分布,损失函数定义为对数损失函数,经验风险最小化就等价于最大似然估计。
 四、信息论
四、信息论
信息论是应用数学的一个分支,主要研究的是对一个信号能够提供信息的多少进行量化。如果说概率使我们能够做出不确定性的陈述以及在不确定性存在的情况下进行推理,那信息论就是使我们能够量化概率分布中不确定性的总量。
1948年,香农引入信息熵,将其定义为离散随机事件的出现概率。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。所以说,信息熵可以被认为是系统有序化程度的一个度量。
 4-1、熵
4-1、熵
如果一个随机变量X的可能取值为,其概率分布为
,则随机变量X的熵定义为H(X):
 4-2、联合熵
4-2、联合熵
两个随机变量X和Y的联合分布可以形成联合熵,定义为联合自信息的数学期望,它是二维随机变量XY的不确定性的度量,用H(X,Y)表示:

4-3、条件熵
在随机变量X发生的前提下,随机变量Y发生新带来的熵,定义为Y的条件熵,用H(Y|X)表示:
条件熵用来衡量在已知随机变量X的条件下,随机变量Y的不确定性。
实际上,熵、联合熵和条件熵之间存在以下关系:
推导过程如下:
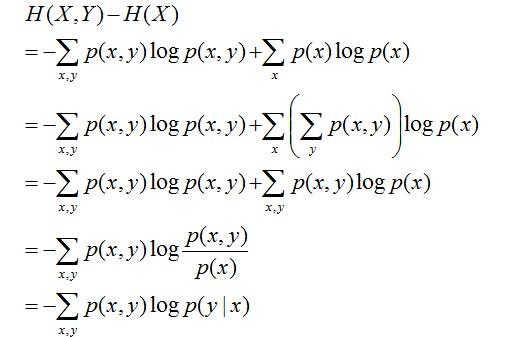 其中:
其中:
- 第二行推到第三行的依据是边缘分布P(x)等于联合分布P(x,y)的和;
- 第三行推到第四行的依据是把公因子logP(x)乘进去,然后把x,y写在一起;
- 第四行推到第五行的依据是:因为两个sigma都有P(x,y),故提取公因子P(x,y)放到外边,然后把里边的-(log P(x,y) - log P(x))写成- log (P(x,y) / P(x) ) ;
- 第五行推到第六行的依据是:P(x,y) = P(x) * P(y|x),故P(x,y) / P(x) = P(y|x)。
 4-4、相对熵
4-4、相对熵
相对熵又称互熵、交叉熵、KL散度、信息增益,是描述两个概率分布P和Q差异的一种方法,记为D(P||Q)。在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中P表示真实分布,Q表示P的拟合分布。
对于一个离散随机变量的两个概率分布P和Q来说,它们的相对熵定义为:
注意:D(P||Q) ≠ D(Q||P)
 4-5、互信息
4-5、互信息
两个随机变量X,Y的互信息定义为X,Y的联合分布和各自独立分布乘积的相对熵称为互信息,用I(X,Y)表示。互信息是信息论里一种有用的信息度量方式,它可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。
互信息、熵和条件熵之间存在以下关系:
推导过程如下:
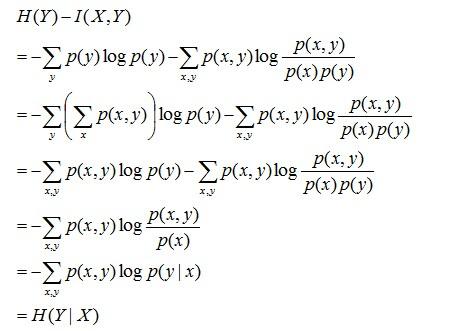 通过上面的计算过程发现有:H(Y|X)
= H(Y) - I(X,Y),又由前面条件熵的定义有:H(Y|X) = H(X,Y) - H(X),于是有I(X,Y)= H(X) + H(Y) - H(X,Y),此结论被多数文献作为互信息的定义。
通过上面的计算过程发现有:H(Y|X)
= H(Y) - I(X,Y),又由前面条件熵的定义有:H(Y|X) = H(X,Y) - H(X),于是有I(X,Y)= H(X) + H(Y) - H(X,Y),此结论被多数文献作为互信息的定义。
 4-6、最大熵模型
4-6、最大熵模型
最大熵原理是概率模型学习的一个准则,它认为:学习概率模型时,在所有可能的概率分布中,熵最大的模型是最好的模型。通常用约束条件来确定模型的集合,所以,最大熵模型原理也可以表述为:在满足约束条件的模型集合中选取熵最大的模型。
前面我们知道,若随机变量X的概率分布是,则其熵定义如下:
熵满足下列不等式:
式中,|X|是X的取值个数,当且仅当X的分布是均匀分布时右边的等号成立。也就是说,当X服从均匀分布时,熵最大。
直观地看,最大熵原理认为:要选择概率模型,首先必须满足已有的事实,即约束条件;在没有更多信息的情况下,那些不确定的部分都是“等可能的”。最大熵原理通过熵的最大化来表示等可能性;“等可能”不易操作,而熵则是一个可优化的指标。





