(java 8)HashMap-红黑树转换-源码解读

 /**
     * Replaces all linked nodes in bin at index for given hash unless
     * table is too small, in which case resizes instead.
     */
    final void treeifyBin(Node<K,V>[] tab, int hash) {
        int n, index; Node<K,V> e;
        // 当前tab容量为空,或者tab数组大小小于64的情况下,不会进行红黑树转换,使用的 resize()代替
        // resize会增加一倍的容量(在当前的基础上),可以看看我这边之前resize()解读的文章
        if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
            resize(); 
        else if ((e = tab[index = (n - 1) & hash]) != null) {
            TreeNode<K,V> hd = null, tl = null;
            do {
            // 构建节点
                TreeNode<K,V> p = replacementTreeNode(e, null);
                if (tl == null)
                    hd = p;
                else {
                    p.prev = tl;
                    tl.next = p;
                }
                tl = p;
            } while ((e = e.next) != null);
            // 树根节点赋值给数组
            if ((tab[index] = hd) != null)
            // 构造红黑树
                hd.treeify(tab);
        }
    }
    
     // For treeifyBin
    TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) {
        return new TreeNode<>(p.hash, p.key, p.value, next);
    }
    
    
   /**
     * Forms tree of the nodes linked from this node.
     * @return root of tree
     * 链表转换成树
     */
    final void treeify(Node<K,V>[] tab) {
        // 树的跟节点
        TreeNode<K,V> root = null;
        // 遍历链表，x指向当前节点、next指向下一个节点
        for (TreeNode<K,V> x = this, next; x != null; x = next) {
            // 下一个节点
            next = (TreeNode<K,V>)x.next;
            // 当前节点的左右节点为空
            x.left = x.right = null;
            // 如果还没有根节点
            if (root == null) {
                // 根节点的父节点为null
                x.parent = null;
                // 根节点为黑色
                x.red = false;
                root = x;
            }
            else {
                // 根节点已存在,获取当前节点的key
                K k = x.key;
                // 当前节点的hash
                int h = x.hash;
                // 当前节点key所属的类类型
                Class<?> kc = null;
                // 从根节点开始遍历
                for (TreeNode<K,V> p = root;;) {
                // dir标识遍历的方向(左右),ph标识当前循环内当前节点的hash
                    int dir, ph;
                    // 当前循环内当前节点的key
                    K pk = p.key;
                    // 如果当前循环内的节点的hash值大于,当前节点(循环外的x节点)的hash值
                    if ((ph = p.hash) > h)
                    // 当前节点x会放到当前遍历到的节点的左侧
                        dir = -1;
                    else if (ph < h)
                    // 否则是右侧
                        dir = 1;
                    // 如果两个节点的hash相同
                    // 如果当前节点x实现了comparable接口,并且当前遍历到的节点和当前节点x是相同class的实例,那么通过comparable在比较一次
                    // 如果还是相等,通过tieBreakOrder进行比较,如果identityHashCode还是一样,最终就会放到左侧
                    else if ((kc == null &&
                              (kc = comparableClassFor(k)) == null) ||
                              // 根据comparable进行比较
                             (dir = compareComparables(kc, k, pk)) == 0)
                        dir = tieBreakOrder(k, pk);
                    // 保存当前遍历到的节点
                    TreeNode<K,V> xp = p;
                    /*
                     * 如果dir 小于等于0 ：当前链表节点一定放置在当前树节点的左侧，但不一定是该树节点的左孩子，也可能是左孩子的右孩子 或者 更深层次的节点。
                     * 如果dir 大于0 ：当前链表节点一定放置在当前树节点的右侧，但不一定是该树节点的右孩子，也可能是右孩子的左孩子 或者 更深层次的节点。
                     * 如果当前树节点不是叶子节点，那么最终会以当前树节点的左孩子或者右孩子 为 起始节点  再从GOTO1 处开始 重新寻找自己（当前链表节点）的位置
                     * 如果当前树节点就是叶子节点，那么根据dir的值，就可以把当前链表节点挂载到当前树节点的左或者右侧了。
                     * 挂载之后，还需要重新把树进行平衡。平衡之后，就可以针对下一个链表节点进行处理了。
                    */
                    if ((p = (dir <= 0) ? p.left : p.right) == null) {
                        // 当前节点的父节点是遍历到的节点 
                        x.parent = xp;
                        if (dir <= 0)
                            // 作为遍历到的节点的左孩子 
                            xp.left = x;
                        else
                            // 作为右孩子
                            xp.right = x;
                        // 执行红黑树新增节点时的平衡操作
                        root = balanceInsertion(root, x);
                        break;
                    }
                }
            }
        }
        // 把所有的链表节点都遍历完之后，最终构造出来的树可能经历多个平衡操作，根节点目前到底是链表的哪一个节点是不确定的
        // 因为我们要基于树来做查找，所以就应该把 tab[N] 得到的对象一定根节点对象，而目前只是链表的第一个节点对象，所以要做相应的处理。
        moveRootToFront(tab, root);
    }
        
     /**
     * Returns x's Class if it is of the form "class C implements
     * Comparable<C>", else null.
     当x的类型为X，且X直接实现了Comparable接口（比较类型必须为X类本身）时，返回x的运行时类型；否则返回null。
     */
    static Class<?> comparableClassFor(Object x) {
        // 判断是否是实现了Comparable接口
        if (x instanceof Comparable) {
            Class<?> c; Type[] ts, as; Type t; ParameterizedType p;
            if ((c = x.getClass()) == String.class) // bypass checks
                // 如果是String类型,直接返回String.class
                return c;
                // 判断是否有直接实现的接口
            if ((ts = c.getGenericInterfaces()) != null) {
                for (int i = 0; i < ts.length; ++i) {
                    if (((t = ts[i]) instanceof ParameterizedType) && // 该接口实现了泛型
                        // 获取接口不带参数部分的类型对象，也就是去掉了泛型参数部分的类型对象。
                        ((p = (ParameterizedType)t).getRawType() ==
                        // 该类型是Comparable
                         Comparable.class) &&
                         // 获取泛型参数数组
                        (as = p.getActualTypeArguments()) != null &&
                        // 只有一个泛型参数，且该实现类型是该类型本身
                        as.length == 1 && as[0] == c) // type arg is c
                        return c;
                }
            }
        }
        return null;
    }

    /**
    * 关于红黑树的特性：
    * 性质1.节点是红色或黑色。
    * 性质2.根节点是黑色。
    * 性质3.每个叶节点（NIL节点，空节点）是黑色的。
    * 性质4.每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
    * 性质5.从任一节点到其每个叶子的路径上包含的黑色节点数量都相同。
    * root 当前根节,x 新插入的节点,返回重新平衡后的根节点
    */
     static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {
            // 新插入的节点标识为红色
            x.red = true;
            //  xp：当前节点的父节点、xpp：爷爷节点、xppl：左叔叔节点、xppr：右叔叔节点
            for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
                // 如果父节点为空、说明当前节点就是根节点，那么把当前节点标为黑色，返回当前节点
                if ((xp = x.parent) == null) {//L1
                    x.red = false;
                    return x;
                }
                //  如果父节点为黑色 或者（父节点为红色 但是 爷爷节点为空）
                //  xp就是根节点时,并且当前树的节点数小于等于3个时,会出现这种情况
                else if (!xp.red || (xpp = xp.parent) == null) // L2
                    return root;
                // 如果父节点是爷爷节点的左孩子 -- 树的左子树
                if (xp == (xppl = xpp.left)) { // L3
                    // 如果右叔叔节点不为空,且是红色
                    if ((xppr = xpp.right) != null && xppr.red) { // L3_1
                        // 右叔叔置为黑色
                        xppr.red = false;
                        // 父节点置为黑色
                        xp.red = false;
                        // 爷爷节点设置为红色
                        xpp.red = true;
                        // 下一轮循环,当前节点变为爷爷节点开始
                        x = xpp;
                    }
                    // 如果右叔叔为空,或者为黑色
                    else {// L3_2
                        // 如果当前节点是父节点的右孩子
                        if (x == xp.right) { //L3_2_1
                            // 父节点左旋
                            root = rotateLeft(root, x = xp);
                            xpp = (xp = x.parent) == null ? null : xp.parent;
                        }
                        // 如果父节点不为空
                        if (xp != null) { // L3_2_2
                            // 父节点 置为黑色
                            xp.red = false;
                            // 爷爷节点不为空
                            if (xpp != null) {
                                // 爷爷节点置为 红色
                                xpp.red = true;
                                // 爷爷节点右旋
                                root = rotateRight(root, xpp);
                            }
                        }
                    }
                }
                // 如果父节点是爷爷节点的右孩子 -- 树的右子树
                else { // L4
                    // 如果左叔叔是红色,和上面的"右叔叔节点不为空,且是红色"的情况类似
                    if (xppl != null && xppl.red) { // L4_1
                        // 左叔叔置为 黑色 
                        xppl.red = false;
                        // 父节点置为黑色
                        xp.red = false;
                        // 爷爷置为红色
                        xpp.red = true;
                        // 下一轮循环,当前节点变为爷爷节点开始
                        x = xpp;
                    }
                    // 如果左叔叔为空或者是黑色 
                    else { // L4_2
                        //  如果当前节点是个左孩子
                        if (x == xp.left) {  // L4_2_1
                            // 针对父节点做右旋
                            root = rotateRight(root, x = xp);
                            xpp = (xp = x.parent) == null ? null : xp.parent;
                        }
                        // 如果父节点不为空
                        if (xp != null) { //L4_2_4
                            // 父节点置为黑色
                            xp.red = false;
                            // 如果爷爷节点不为空
                            if (xpp != null) {
                                // 爷爷节点置为红色
                                xpp.red = true;
                                // 针对爷爷节点做左旋
                                root = rotateLeft(root, xpp);
                            }
                        }
                    }
                }
            }
        }
    
/**
 * 节点左旋
 * root 根节点
 * p 要左旋的节点
 */
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
                                              TreeNode<K,V> p) {
    TreeNode<K,V> r, pp, rl;
    if (p != null && (r = p.right) != null) { // 要左旋的节点以及要左旋的节点的右孩子不为空
        if ((rl = p.right = r.left) != null) // 要左旋的节点的右孩子的左节点 赋给 要左旋的节点的右孩子 节点为：rl
            rl.parent = p; // 设置rl和要左旋的节点的父子关系【之前只是爹认了孩子，孩子还没有答应，这一步孩子也认了爹】
 
        // 将要左旋的节点的右孩子的父节点  指向 要左旋的节点的父节点，相当于右孩子提升了一层，
        // 此时如果父节点为空， 说明r 已经是顶层节点了，应该作为root 并且标为黑色
        if ((pp = r.parent = p.parent) == null) 
            (root = r).red = false;
        else if (pp.left == p) // 如果父节点不为空 并且 要左旋的节点是个左孩子
            pp.left = r; // 设置r和父节点的父子关系【之前只是孩子认了爹，爹还没有答应，这一步爹也认了孩子】
        else // 要左旋的节点是个右孩子
            pp.right = r; 
        r.left = p; // 要左旋的节点  作为 他的右孩子的左节点
        p.parent = r; // 要左旋的节点的右孩子  作为  他的父节点
    }
    return root; // 返回根节点
}
 
/**
 * 节点右旋
 * root 根节点
 * p 要右旋的节点
 */
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
                                               TreeNode<K,V> p) {
    TreeNode<K,V> l, pp, lr;
    if (p != null && (l = p.left) != null) { // 要右旋的节点不为空以及要右旋的节点的左孩子不为空
        if ((lr = p.left = l.right) != null) // 要右旋的节点的左孩子的右节点 赋给 要右旋节点的左孩子 节点为：lr
            lr.parent = p; // 设置lr和要右旋的节点的父子关系【之前只是爹认了孩子，孩子还没有答应，这一步孩子也认了爹】
 
        // 将要右旋的节点的左孩子的父节点  指向 要右旋的节点的父节点，相当于左孩子提升了一层，
        // 此时如果父节点为空， 说明l 已经是顶层节点了，应该作为root 并且标为黑色
        if ((pp = l.parent = p.parent) == null) 
            (root = l).red = false;
        else if (pp.right == p) // 如果父节点不为空 并且 要右旋的节点是个右孩子
            pp.right = l; // 设置l和父节点的父子关系【之前只是孩子认了爹，爹还没有答应，这一步爹也认了孩子】
        else // 要右旋的节点是个左孩子
            pp.left = l; // 同上
        l.right = p; // 要右旋的节点 作为 他左孩子的右节点
        p.parent = l; // 要右旋的节点的父节点 指向 他的左孩子
    }
    return root;
}

红黑树转换图例:

1、无旋转

 

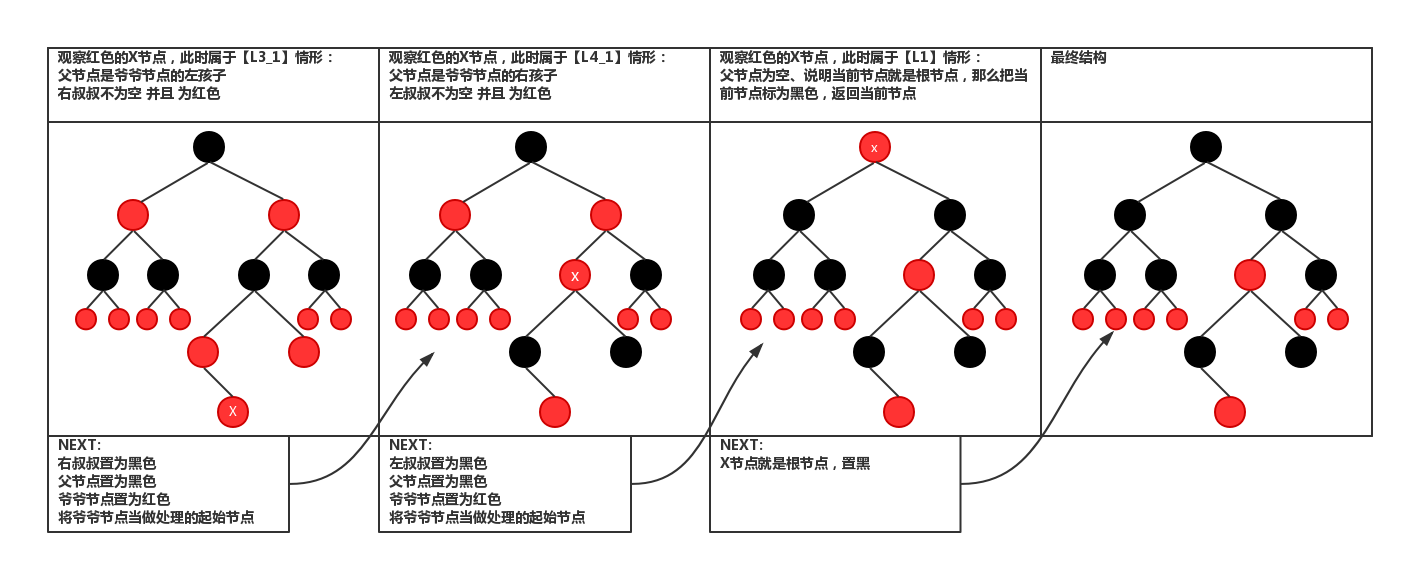
 2、有旋转

 

 

 

 

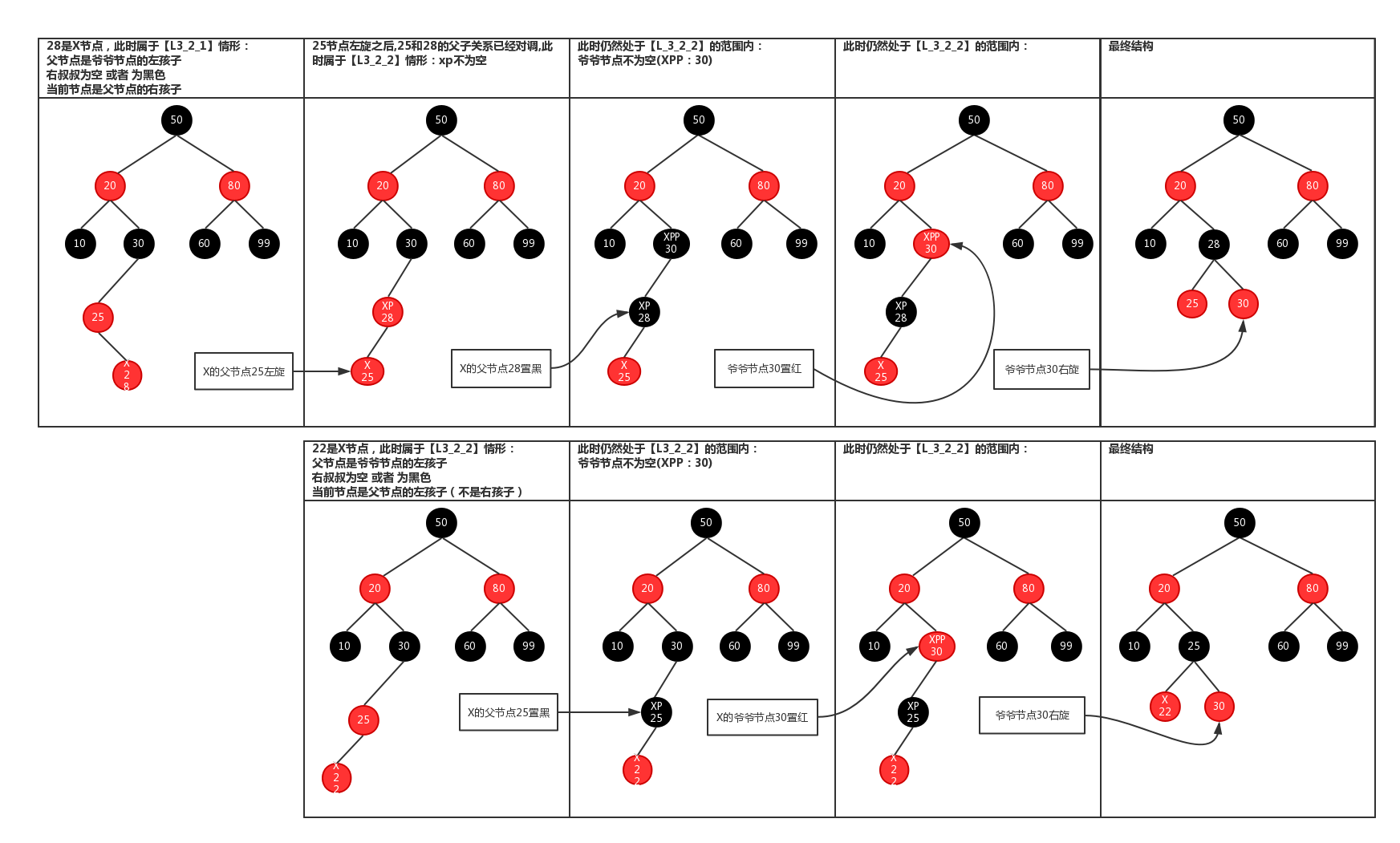
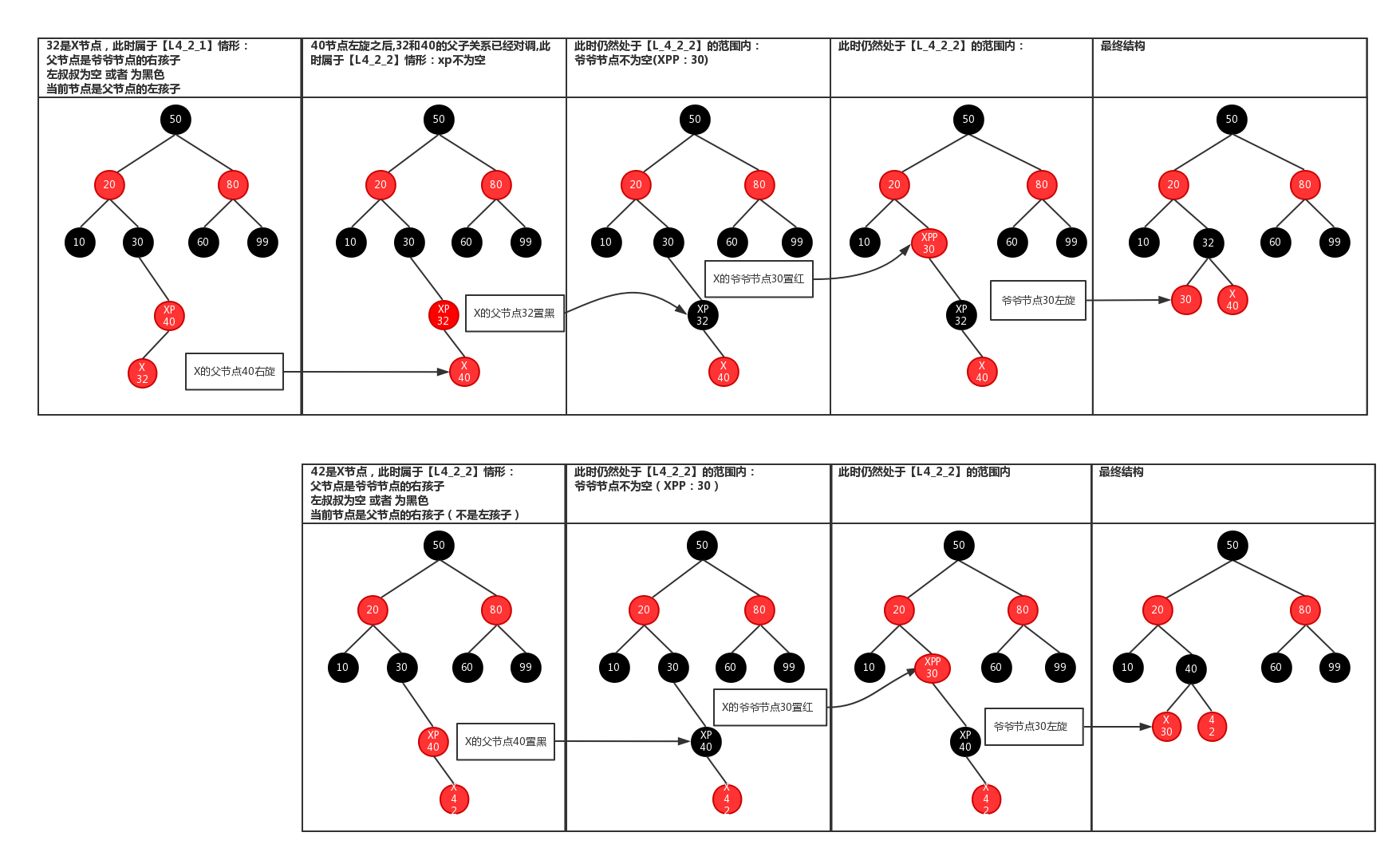
参考:https://blog.csdn.net/qpzkobe/article/details/79533237

参考:https://blog.csdn.net/weixin_42340670/article/details/80531795

参考:https://blog.csdn.net/weixin_42340670/article/details/80531795