[图论 , 线性基 , 9.28模拟赛] 图异或
图异或
题意
给定一张 \(n\) 个点 \(m\) 条边的连通二分图,每个点有点权 \(a_i\)。\(Q\)组询问,每次给定两个点\(u,v\),求点 \(u\) 到点 \(v\) 的路径(不一定要简单)权值最大值。路径的权值定义为经过的所有点的异或和,同一个点经过多次则计算多次。
解法
一看题面 , 容易联想到 [WC2011]最大XOR和路径 , 都属于图上任意游走(而非走法固定,即不要求是简单路径) , 利用异或的自反性是解决此类异或和最大问题的关键.
\(O(nmq)\) 的解法看起来没什么启发意义 , 我们按下不表.
先画几个图 , 我们容易发现走过一个环即 \(p_1->p_2->p_3->...p_1\) 这样的情况的时候,除了入点以外的点均产生了贡献.
但是这个性质略微看起来不优 , 我们难以处理一个环强制去除一个点后的状态 , 因为若干个简单环的嵌套会导致状态数异常地多.换个思路?精细化处理?
答案是精细化处理,那不妨小小地手搓一下若干个个简单环的嵌套.
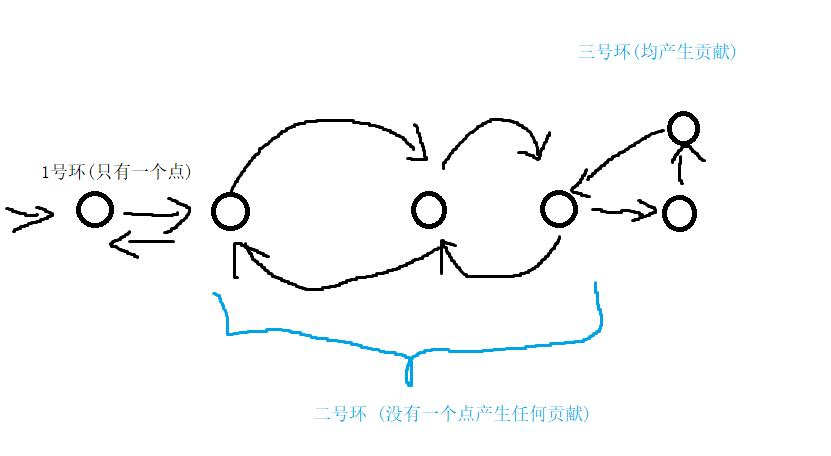
注意到仅有 1号环 与 3号环 产生了贡献 , 而且内部的点均产生贡献(访问了一次), 而 2号环 未产生贡献 (访问了两次)
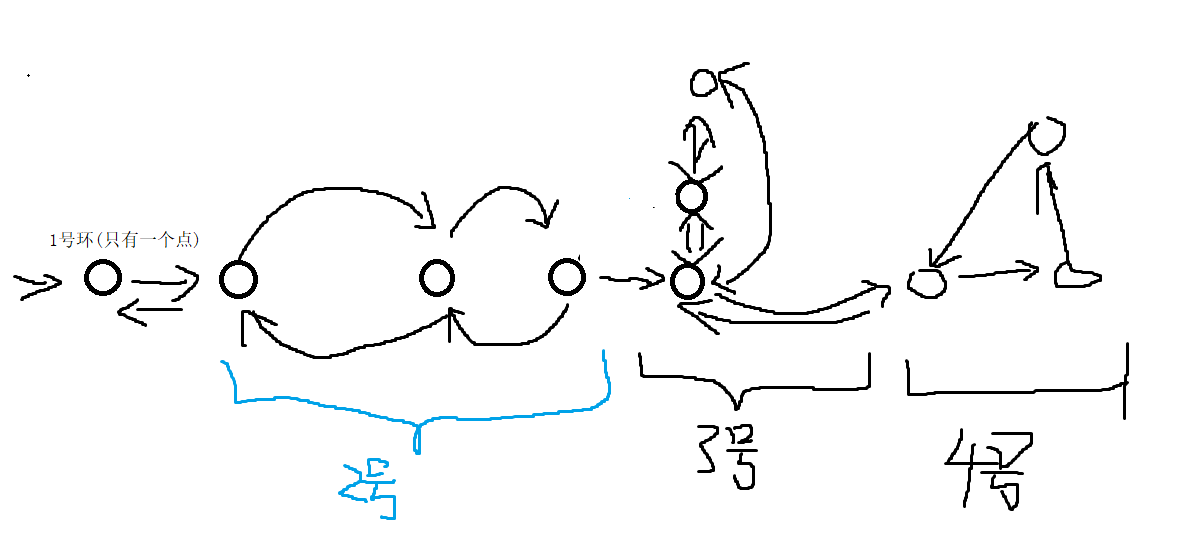
注意到仅有 1号环 与 4号环 产生了贡献 , 而且内部的点均产生贡献(访问了一次), 而 2号环和4号环 未产生贡献 (访问了偶数次)
我们能得到一个结论 仅有起点和终点所在简单环产生贡献.
证明 : 我们将简单环缩成一个整体用 \(c_i\) 表示,那么路径形如 \(c_1 -> c_2 ->... ->c_{n-1}->c_n -> c_{n-1} -> ... -> c_2 -> c_1\).
显然仅有起点和终点所在环产生贡献
这是有向图的情况 , 无向图意味着环的构造更加简易,我们甚至可以将一条边和两个路径看作两个简单环的拼凑
结合上述性质(经过若干个简单环 , 有且仅有起点和终点的环产生贡献) , 我们考虑构造一个较为简易的路径 : 即从起点出发走到某点后原路返回 , 路径形如 \(p_1 -> p_2 ->... ->p_{n-1}->p_n -> p_{n-1} -> ... -> p_2 -> p_1\) 贡献为 \(val_{p_1} \oplus val_{p_n}\)
重新表述一下我们的策略:从起点出发走到某点后原路返回,可以得到该链两个端点的异或作为贡献.
原图保证联通,也就是说我们可以从起点出发,获得若干点的异或值后再回到起点,最后再走向终点.
这里有个小问题 : 路径的起点也会产生贡献 , 用以上策略 + 线性基 我们难以确定起点的状态.
我们按上述策略走偶数次,则起点贡献不变.走奇数次,则起点贡献改变了.
一个思路就是我们强制选取偶数次 , 再强制选择奇数次.并将答案取个 max.
对于偶数次 , 我们构造性的得到一个数组 \(B\) , \(B_i = val_i \oplus val_{i+1},(i < n)\) .由于 \((a \oplus b) \oplus(a \oplus c)=b \oplus c\),我们可以通过若干个 \(B\) 的异或得到任意我们想要点对集合.对 \(B\) 张成一个线性基,就可以得到偶数次的最优解.
对于奇数次 , 我们强制加入任意一个与起点 \(u\) 不同的点的权值并消除 \(u\) 的贡献,由于 \((a \oplus b) \oplus(a \oplus c)=b \oplus c\) 的性质,此时线性基可以表示任意一个点异或上偶数个数的数的集合.
至此 , 策略的问题讲完了.
梳理一下我们该做什么.
- 处理 \(B\) 序列,并张成一个线性基
- 求出一段路径的异或和 , 并分奇偶讨论.
解决了第一步,讲讲第二步.
单次 \(O(logn)\) 求得路径
对原图建立任意一个生成树 , 通过链上前缀和得到路径异或和.
\(pre_u \oplus pre_v \oplus pre_{fa[lca_{u,v}]}\)
\(pre\) 表示到根节点的链上异或和.
瓶颈在于求LCA , 你用四毛子变成 \(O(n) - O(1)\) 或者 ST表 也可以.但是倍增够用了
至此,我们并不依赖于二分图的性质就解决了这个问题.
单次 \(O(0)\) 求得路径(因为没必要QAQ)
我们没用上二分图的性质啊.
若两个点不在同一部 , 则起点与终点路径长度必定为偶数. 若两点在同一部 , 则路径长度必定为奇数.
对于长度为偶数的路径我们对 \(0\) 跑个最值即可 , 因为偶数个点总是能在线性基中被抵消/被补偿.
对于长度为奇数的路径我们对 \(val_u\) 跑个最值即可 , 选择某个点, 剩下就转化成偶数个了
联系与练习:
[WC2011]最大XOR和路径

