图论入门

僕の图论本当苦手,何の事僕に適当作る？

Topo sort

定义&性质
image
————OI wiki

求法就是朴素选取入度为0的点，将其加入答案序列的末端。根据选取模式的不同可以得到不同的topo序
时间复杂度 \(O(n+m)\)

性质 & 应用：

  1. 基于定义性质的直接应用

    例题1：CF721C
    题意： 给出一个 \(n\) 个点 \(m\) 条边的有向无环图。问从 \(1\) 到 \(n\) ，在距离不超过 \(k\) 的情况下最多经过多少点，并输出一个方案。
    解法： 先进行拓扑排序，则拓扑序排在 \(u\) 后的点 \(v\) 均不可能到达 \(u\)。使得DP满足了无后效性，于是直接朴素记录路径进行DP即可。

    例题2：CF1385E
    题意： 给你一张图，有些边是有向边，有一些是无向边，让你给无向边添上方向，使这张图成为一个有向无环图。
    解法： 根据拓扑序的性质，一个DAG上的边，必然由拓扑序小的点指向拓扑序大的点，其实这是充要条件。于是先对有向边进行拓扑排序，然后剩下的点拓扑序任意调整，最后按上面方法构造即可。

  2. 基于构造方法的应用

    例题1：LuoguP7054
    题意： 给定一张 \(n\) 点 \(m\) 条边的有向无环图，你可以至多添加 \(k\) 条有向边，使得这仍然是一个有向无环图，使得字典序最小的拓扑序的字典序尽量大。输出这个拓扑序以及方案。
    解法：
    考虑如何确定字典序最小的拓扑序？
    即普通拓扑排序过程中，用小根堆储存入度为 \(0\) 的点，每次取堆顶即可。
    手中有加边的机会，意味着我们可以让这个小根堆堆顶元素放到某些待加入的点后部，或者放我们想要的元素到小根堆中。
    更具体的，我们维护两个集合 \(u,v\) ，\(u\) 表示此时入度为零的集合， \(v\) 表示我们加了边延后放的集合,\(u\) 用小根堆维护,\(v\) 用大根堆维护。
    接下来就是分类讨论：

    1. 若 \(siz_u>1\) 且 \(k>0\)。则往拓扑序中放入 \(u\) 堆顶元素一定不如放入 \(u\) 中其他的元素，则将 \(top_u\) 放入 \(v\) 中即可，并令 k-=1;
    2. 若 \(siz_u=1\) 。比较 \(u\) \(v\) 堆顶元素大小，放入较大的元素即可。
    3. 若 \(siz_u=0\) 只能放入 \(v\) 堆顶元素了。
      此时就是最优的拓扑序，至于构造，从 \(v\) 中弹出元素时和拓扑序前一个元素连边即可。

    例题2：LuoguP4099
    题意： 给定一张树形图，求拓扑序数量。
    解法：
    树形图，直接当成树就可以了罢！
    我们并不关心具体的拓扑序长什么样子。只在乎如何能够唯一表示。
    直接设 \(f_{i,j}\) 表示此时 \(i\) 点在已处理序列中排名第 \(j\) 的方案数，显然此时可以做到不重不漏。
    转移过程直接枚举 \(u,v\) 的排名，分类讨论讨论就出来辣！！！
    顺便考察了前缀和优化，动手写写叭。

  3. 难以分类的妙妙题
    例题1：ARC083F
    题意： 平面直角坐标系上有 \(2n\) 个小球，坐标为 \((x_i,y_i)\)。其中 \(y=0,x=1,2,...,n\) \(y=1,2,...,n,x=0\) 处都有一个机器人。\(y=0\) 的机器人向 \(y\) 的正方向前进，\(x=0\) 的机器人向 \(x\) 的正方向前进。每个机器人遇见第一颗小球就会同归于尽。
    求有多少种机器人出场的排列，使得场面上小球和机器人都GG了。
    解法:
    一个常见的思路就是建立二分图，将行列变为两个部分的点，元素作为边。
    一个连通块有解，当且仅当边数等于点数。
    形成了一个基环树森林，然后你可以任意定向边。问题转化成了求拓扑序数量。
    稍作分析，则环点必定被相邻环点支配，非环点必定被非环点支配。
    因此环上只有两种解，枚举这两种解。
    然后推推可得一个基环树的答案为
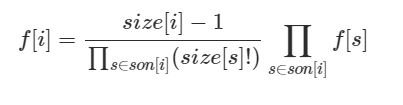
    image

MST （最小生成树）相关

定义： 边权和最小的生成树。
性质：

  1. 若有多颗不同的最小生成树。则相同权值边的数量和作用相同。此作用指沟通哪些连通块。
  2. 最小生成树是最小瓶颈生成树的充分不必要条件。
  3. 任意两点在最小生成树路径的最大边权，和两点在原图的最小瓶颈路的权值相同。
  4. 合并两个图（指仅仅添加边，两个图的点的标号集合为相等或包含关系），可以只用两个图最小生成树的边。
    以上均可以用贪心证明，我就不证了。

构造：
贪心。
每次选取能选取的不会连成环的最短的边/每次选取与当前连通块最近的点/每次选取某个连通块连出的最短边。
就是 Kruskal Prim 和 某B开头的最小生成树算法在最小生成树上的应用。
不必多说（？

应用:

例题1：严格次小生成树
题意： 字面意思，生成一颗总边权严格大于最小生成树的树，且保证除最小生成树外任何生成树的总边权均小于它。
解法： 先生成一颗最小生成树。
严格次小生成树有且只有一条边和最小生成树不同。粗略证明一下，就是如果变更两条边，则边权的变化量就大于只有一条边的变化量。
于是枚举每一条非树边，试图替换树上的边。
我们要换的话，必然是换环上的最小的大于待加入边权值的边，树剖维护最大边和次大边即可。
非严格次小生成树就是只维护最大边。

例题2：最小度限制生成树
题意： 给你一个有 \(n\) 个节点，\(m\) 条边的带权无向图，你需要求得一个生成树，使边权总和最小，且满足编号为 \(s\) 的节点正好连了 \(k\) 条边。
解法： WQS二分？ 不！这是MST专题！！！
此下讨论默认无重边。
先考虑如何判定无解。即编号为s的点在任何一颗生成树上的度数 \(\neq k\)
先建出没有 \(s\) 的最小生成森林。
若连通块数量大于 \(k\) 或者某一连通块无法与 \(s\) 相连（最小度数大于 \(k\)，原图不联通），则非法。
然后数边数，若与 \(s\) 相连的边数数量小于 \(k\) 则非法。
若不满足上面的任何一种情况，则一定有解。可以把非与 \(s\) 相连的边改成与 \(s\) 相连的边，从而调整度数。
接着考虑如何构造。
先建出没有 \(s\) 的最小生成森林。（就是尽可能多连边，形成尽量大的森林）
然后加入 \(s\) 点。用 \(Boruvka\) 的思想，每个连通块伸出一条最小权的边与 \(s\) 相连。
形成一颗满足 \(s\) 的度数最小的最小生成树
我们加入与 \(s\) 相连的边，可以看作是断开一条森林中的边，让他的父亲变成 \(s\)。
可以发现换不换边，不同的点不会相互干扰。
因此直接选择变化量最小的加边方式，然后大力连边即可。

例题3：P4208 [JSOI2008]最小生成树计数
题意： 字面意思，最小生成树计数。
解法： 用了一个性质。“若有多颗不同的最小生成树。则相同权值边的数量和作用相同。此作用指沟通哪些连通块。”
那做法就很明朗了，求出任意一颗最小生成树。然后把某个权值的边删掉，然后原图进行缩点。然后矩阵树定理直接杀穿。当然，你嗯要枚举相同权值的边，也没问题。

例题4：【BZOJ3714】Kuglarz（最小生成树）
题意： 魔术师的桌子上有n个杯子排成一行，编号为1,2,…,n，其中某些杯子底下藏有一个小球，如果你准确地猜出是哪些杯子，你就可以获得奖品。花费\(c_{i,j}\)元，魔术师就会告诉你杯子i,i+1,…,j底下藏有球的总数的奇偶性。
采取最优的询问策略，你至少需要花费多少元，才能保证猜出哪些杯子底下藏着球？
解法：
知道(1,l-1) （1,l) 的奇偶性，不难知道 l 下面是否有杯子。
那奇偶性支持区间合并，即 (1,l) (l+1,r) 可以推出 (1,r) 。
最终的目标就是知道所有(1,1...n)
看起来是要构成连通块？
最小生成树。

克鲁斯卡尔重构树会放到后面写。顺便写写leafy tree？
还有一系列MST的优化构造问题。例如 河童重工 之类的...

最短路相关

分为单源最短路，全源最短路
单源最短路 常见算法就是 Dijkstra 和 spfa（队列优化bellman-ford）
全源最短路 有弗洛伊德。或者跑n次dij/spfa。对于负边权可以考虑原始对偶。算法这里不赘述
说起来，有人要看我的（堆&队列随机优化bellman-ford） 吗（

posted @ 2022-04-11 09:29  Hencecho  阅读(84)  评论(0)  编辑  收藏  举报