一类用以解决凸性折线背包的Trick

引子:[P4331 [BalticOI 2004]Sequence 数字序列]
(https://www.luogu.com.cn/problem/P4331 "P4331 [BalticOI 2004]Sequence 数字序列")
出自黄源河的《左偏树的特点及其应用》,算是最早的引进(?
题面
给定一个整数序列 \(a_{1}, a_{2}, \ldots, a_{n}\) , 求一个不下降序列 \(b_{1} \leq b_{2} \leq \ldots \leq b_{n}\) , 使得数 列 \(\left\{\mathrm{a}_{\mathrm{i}}\right\}\) 和 \(\left\{\mathrm{b}_{\mathrm{i}}\right\}\) 的各项之差的绝对值之和 \(\left|\mathrm{a}_{1}-\mathrm{b}_{1}\right|+\left|\mathrm{a}_{2}-\mathrm{b}_{2}\right|+\ldots+\left|\mathrm{a}_{\mathrm{n}}-\mathrm{b}_{\mathrm{n}}\right|\) 最小。
其中 \(1\leq n \leq 10^6 , 0 \leq a_i \leq 2\times 10^9\)
做法
首先 ,对于这种使序列严格递增的题,我们考虑将 \(a_i,b_i\) 同时减 \(i\),保证 \(|a_i-b_i|\) 不变的同时,将原问题弱化为使序列不降。
\(O(n^2)\)
采用DP,令 \(f_{i,j}\) 表示目前已经解决了 \(a_i\) ,\(b_i\) 目前所填的数为 \(j\)时的最小代价。
有转移\(f_{i, j}=\min _{k \leq j} \{f_{i-1, k}+\left|a_{i}-j\right|\}\)。
至于打印方案,使用代价递推即可
\(O(nlogn)\)
该类做法计算的是一类转移条件代价 满足以下条件的DP:
- 连续
- 为分段线性函数
- 同时为凸或者同时为凹 (为了方便,接下来讨论的转移代价皆为凸性函数,凹性类推即可)
对于一段形如
\(f(x)=\left\{\begin{array}{rr}
-x-3 & (x \leq-1) \\
x & (-1<x \leq 1) \\
2 x-1 & (x>1)
\end{array}\right.\)
可以通过仅记录最后一段函数 \(f_r(x)=2x-1\),与转折点集合 \(L=\{ -1,-1,1\}\)(经过转折点,斜率变化量为 \(1\) .若变化量不为一,则设立多个相同转折点)
可以发现,由于函数连续,只要得知了最后一段函数,以及转折点集合,就可以获取函数的所有信息。
(由于函数满足凸性,因此转折点集合一定可以表示导函数变化)
推理性质:
设 \(F(x),G(x)\) 均为满足上述条件的分段线性函数。则 \(H(x)=F(x)+G(x)\) 也为满足上述条件的分段线性函数,且有 \(H_r(x)=F_r(x)+G_r(x)\) 以及 \(L_{H}=L_{F} \cup L_{G}\) 。
粗略证明一下,就是 \(F,G\) 的导函数满足递增/递减,则 \(H\) 的导函数也满足递增/递减。
且导函数的变化与 \(L\) 对应。
回归问题。
优化转移
\(f_{i, j}=\min _{k \leq j} \{f_{i-1, k}\}+\left|a_{i}-j\right|\)
令 \(F_i(x)=f_{i,x},G_{i}(x)=\min _{k \leq x} \{f_{i-1, k}\}=\min _{k \leq x} \{F_{i-1}(k)\}\)
得到转移 \(F_i(x)=G_{i} + \left | x-a_i \right |\)
易得 \(F_i(x)=0,G_i(x),\left | x-a_i \right |\) 均为满足上述条件的线性函数。
\(G_i\) 是 \(F_i\) 的前缀min。
由于 \(F_i\) 满足凸性,可得
$\left\{\begin{matrix} G_i(x)=F_i(x) (F'_i(x)\leq 0)\\ G_i(x)=MINN (F'_i(x) > 0)\end{matrix}\right. $
其中 \(MINN\) 为 \(F_i'(x)=0\) 时 \(F_i(x)\) 的取值,(\(F\) 满足凸性,当斜率 \(=0\) 时,即为最小值).
画个图。
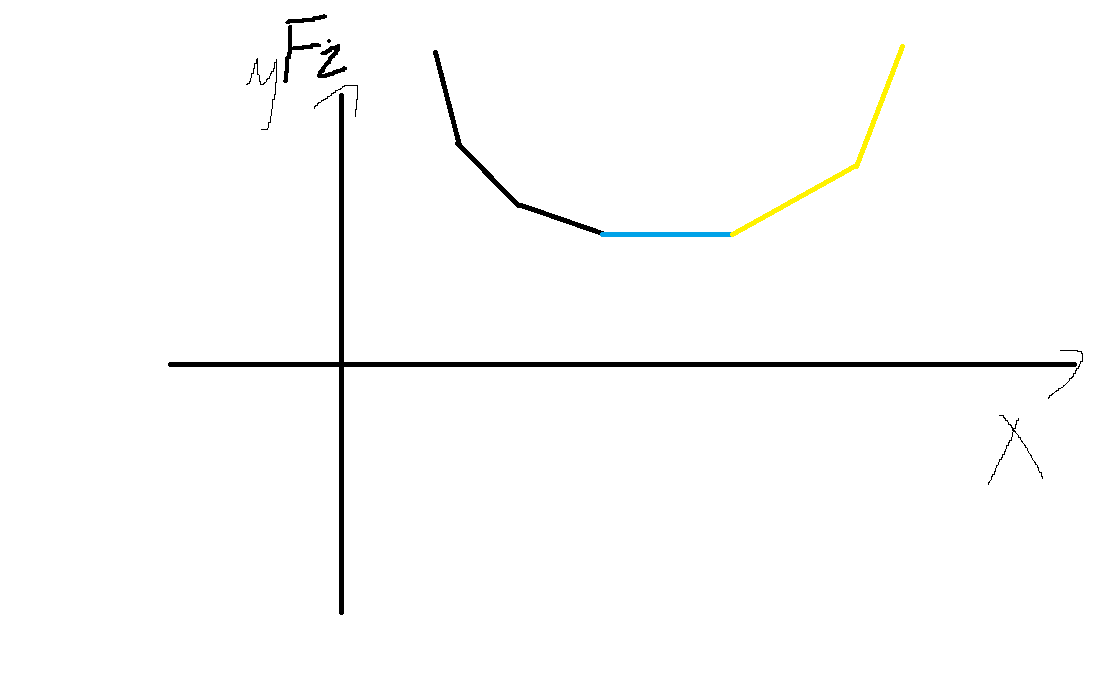
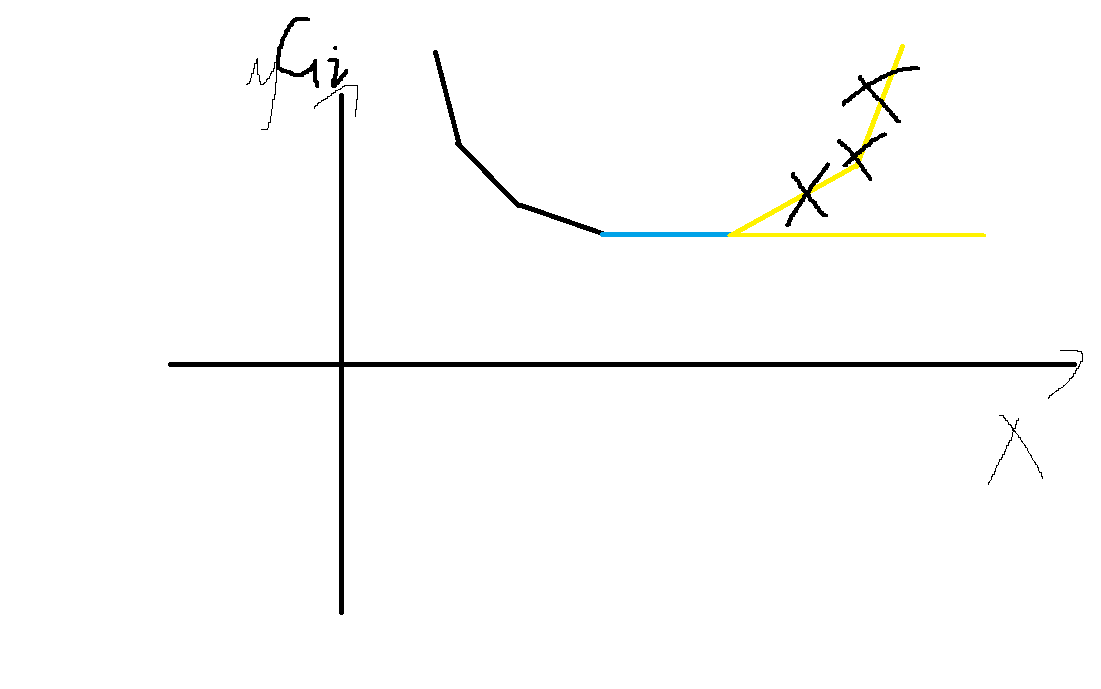
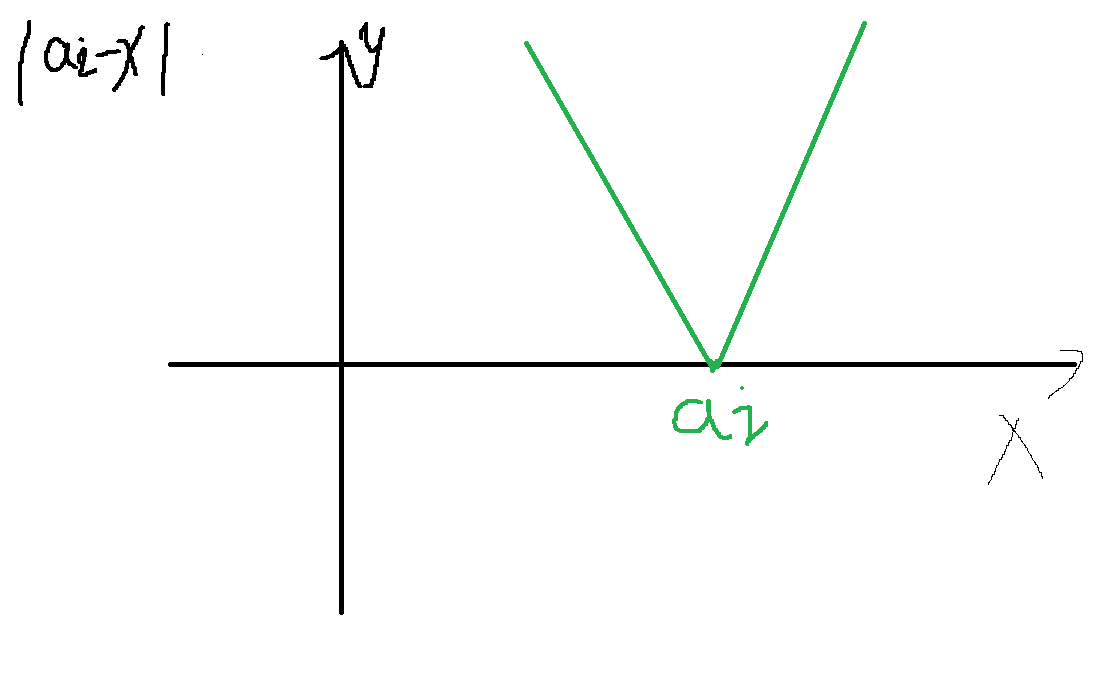
考虑加上 \(\left | x-a_i \right |\) 后的结果。
即为加入了两个分段点 \(\{ a_i , a_i \}\)
因而 $ G_{i}$ 各段的函数斜率形如 \(\{\ldots-3,-2,-1,0\}\) ,加上 \(\left|x-a_{i}\right|\) 后斜率变为 \(\{\ldots-3,-2,-1,0,1\}\) ,因而需要删除末尾的分段点。
弹出最右侧的分段点即可。(加入的分段点不一定是最右侧)
具体的,我们可以维护一个大根堆,每次插入两个分段点,然后弹出最右侧的分段点即可。
此时的堆即表示新的 \(F_i\)
至此就结束了。代码其实意外好写。
点击查看代码
using namespace std;
const int maxn =1e6+10;
int n;
priority_queue <int> q;// 维护分段点
int a[maxn];
ll ans=0,ans2=0;
int qaq[maxn];
signed main()
{
#ifndef ONLINE_JUDGE
freopen("txt.in", "r", stdin);
freopen("txt.out", "w", stdout);
#endif
cin >> n;
fo (i,1,n)
{
cin >> a[i];
a[i]-=i;
q.push(a[i]);
ans+=q.top()-a[i]; // |x-a[i]| 为定值,此时取G的最小值最优
q.push(a[i]);
q.pop();
qaq[i]=q.top();
}
cout<<ans<<endl;
fd (i,n-1,1) qaq[i]=min(qaq[i+1],qaq[i]);
fo (i,1,n)
{
cout<<qaq[i]+i<<" ";
}//反着递推求得答案
return 0;
}


